Для описания алгоритмов работы дискретных устройств необходим соответствующий математический аппарат. Такой математический аппарат в XIX веке разработал ирландский математик Джон Буль, и теперь его называют булевой алгеброй (алгеброй логики). Булева алгебра оперирует двумя понятиями: событие истинно (логическая единица – лог. 1) или событие ложно (логический нуль – лог. 0). Эти два понятия называются константами алгебры логики.
Логические переменные могут принимать одно из двух значений констант:
х = 0, если х ¹ 1;
х = 1, если х ¹ 0.
Над логическими константами и переменными можно совершать логические операции: логическое сложение, логическое умножение и отрицание (инверсию).
Логическое сложение: операция ИЛИ (дизъюнкция). Правило логического сложения для двух переменных представлено в таблице 1.2.
Таблица 1.2
Правило операции логического сложения
| Х1 | Х0 | Х1 + Х0 (Х1 V X0) |
Операция логического сложения справедлива для любого числа переменных и соответствует математической операции объединения множеств. Число переменных, над которыми проводится операция, обозначается цифрой, стоящей перед обозначением операции. Для данного примера получаем запись 2ИЛИ.
|
|
|
Логическое умножение: операция И (конъюнкция). Правило логического умножения для двух переменных представлено в таблице 1.3.
Таблица 1.3
Правило операции логического умножения
| Х1 | Х0 | Х1 × Х0 (Х1 L X0) |
Операция логического умножения также справедлива для любого числа переменных и соответствует математической операции пересечения множеств. Число переменных, над которыми проводится операция, также обозначается цифрой, стоящей перед обозначением операции. Для данного примера получаем запись 2И.
Отрицание (инверсия): операция НЕ. Операция обозначается горизонтальной чертой над переменной (или над выражением, содержащим несколько переменных) и определяется правилом:
если 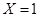 , то
, то 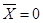 ;
;
если 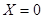 , то
, то 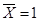 .
.
Логические элементы. В соответствии с перечнем логических операций различают три основных логических элемента (ЛЭ): И, ИЛИ, НЕ. Условные графические обозначения логических элементов представлены на рис. 1.2.

Рис. 1.2. Условные графические обозначения логических элементов
Число входов элементов И и ИЛИ может быть произвольным. Элемент НЕ всегда имеет только один вход.
 2014-01-31
2014-01-31 1022
1022
