Как и в парной зависимости возможны различные виды множественной регрессии: линейные и нелинейные. В виду четной интерпретации параметров наиболее широко используются линейная и степенные функции.
В уравнении множественной регрессии:
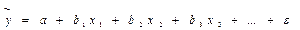
Коэффициенты при х называются коэффициентами «условно чистой» регрессии. Они показывают среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
Коэффициенты «условно чистой» регрессии, (b j) являются именованными числами, выраженными в различных единицах измерения (в тех же единицах, что и соответствующие им факторы). Поэтому они не сравнимы друг с другом, т.е. по их величине нельзя сделать вывод, какой из факторов в наибольшей степени влияет на результат.
Параметр а не подлежит экономической интерпретации.
Анализ уравнения регрессии и методика определения его параметров становятся более наглядными, а расчеты существенно упрощаются, если воспользоваться матричной формой записи этого уравнения. Так, уравнения вида
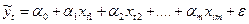 (4.6)
(4.6)
можно записать следующим образом:
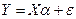 ,
,
где Y – вектор зависимой переменной размерности (n х 1), представляющий собой n наблюдений значений yt.
X – матрица независимых переменных, элементы которой суть n x m наблюдения значений независимых переменных X1, X2, …, Xm размерность данной матрицы равна (n x m);
α – подлежащий оцениванию вектор неизвестных параметров размерности (m х 1);
ε – вектор случайных отклонений (возмущений) размерности (n х 1).
Таким образом,
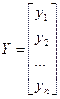
| Х = |   1 x11.... x1m
1 x21.... x2m
................
1 xn1.... xnm 1 x11.... x1m
1 x21.... x2m
................
1 xn1.... xnm
| 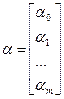
|
Уравнение (4.6) содержит значения неизвестных параметров α0, α1, α2, …, αm. эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров представлены их оценки (а именно такие регрессии и применяются на практике), имеют вид:
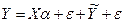 (4.7)
(4.7)
где α – вектор оценок параметров;
ε – вектор «оцененных» отклонений регрессии, ε = Y – Xα – остатки регрессии;
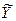 – оценка значений Y, равная Xα.
– оценка значений Y, равная Xα.
Для оценивания неизвестного вектора параметров α воспользуемся методом наименьших квадратов (МНК). Формула для вычисления параметров регрессионного уравнения имеет вид:
α = (ХТХ)-1ХТУ (4.8)
Можно воспользоваться и другим способом оценки неизвестных параметров регрессионного уравнения.
Для линейных моделей и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которых позволяет получить оценки параметров регрессии:
Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которых позволяет получить оценки параметров регрессии:
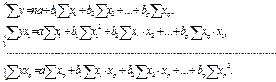
 (4.9)
(4.9)
для ее решения может быть применен метод определителей:
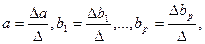 (4.10)
(4.10)
где 
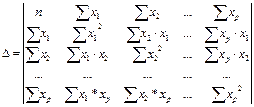 - определитель системы.
- определитель системы.
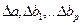 - частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
- частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:
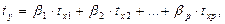 (4.11)
(4.11)
где 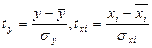 - стандартизованные переменные;
- стандартизованные переменные;
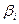 - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии.
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор xi изменится на 1 сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе воздействия их на результат. Смысл стандартизированных коэффициентов βj позволяет использовать их при отсеве факторов, т.е. из модели исключаются факторы с наименьшим значением βj.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (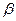 -коэффициенты) определяются из следующей системы уравнений:
-коэффициенты) определяются из следующей системы уравнений:
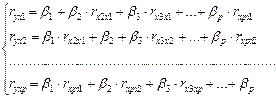 (4.12)
(4.12)
Связь коэффициентов множественной регрессии bi со стандартизованными коэффициентами 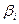 описывается соотношением:
описывается соотношением:
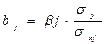 (4.13)
(4.13)
Параметр a определяется следующим образом:
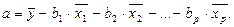 (4.14)
(4.14)
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:
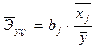 (4.15)
(4.15)
Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.
Для расчета частных коэффициентов эластичности применяются следующая формула:

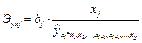 (4.16)
(4.16)
 2014-02-01
2014-02-01 840
840








