Множественная линейная регрессия

Множественный регрессионный анализ является расширением парного регрессионного анализа на случай, когда зависимая переменная гипотетически связана с более чем одной независимой переменной. В этом случае возникает новая проблема, которой не было в случае парной модели. При оценке влияния данной независимой переменной на зависимую переменную нам надо будет разграничить воздействие на зависимую переменную ее и другие переменные. Кроме того, мы должны будем решить проблему спецификации модели. Если в парном регрессионном анализе эта проблема заключалась только в выборе вида функции f (Х), то теперь нам, кроме этого, надо будет решить, какие мы будем включать в модель, а какие – нет. Иначе говоря, если предполагается, что несколько переменных могут оказывать влияние на зависимую переменную, то другие могут и не подходить для нашей модели.

Итак, у нас есть независимая переменная Y, которая характеризует состояние или поведение экономического объекта, и есть набор переменных X ₁,…, X_k, характеризующие этот экономический объект качественно или количественно, которые, как мы предполагаем, оказывают влияние на переменную Y, т. е. мы предполагаем, что значения результирующей переменной Y выступают в виде функции, значения которой определяются. правда, с некоторой погрешностью, значениями объясняющих переменных, выступающих в роли аргументов этой функции, т. е.

Y = f (X ₁,…, X_k) + e,

где e - случайный член, который входит в наше уравнение по тем же самым причинам, что и в случае парного регрессионного анализа.

Поначалу, среди всех возможных функций f (Х ₁,…, Х_k) мы выбираем линейные:

(*)

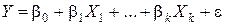(*) – множественная линейная регрессионная модель (МЛРМ) со свободным членом.

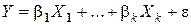- МЛРМ без свободного члена.

Например, если мы изучаем величину спроса на масло, то модель может выглядеть следующим образом:

,

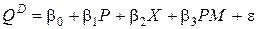где Q^D - объем спроса на масло, Х - доход, P - цена на масло, PM - цена на мягкое.

Здесь нам неизвестны коэффициенты b и параметры распределения e, Зато мы имеем выборку из N наблюдений над переменными Y и X ₁,…, X_k. Для каждого наблюдения должно выполнятся следующее равенство:

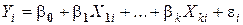
или в матричной форме:

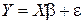, где

, , , .

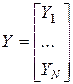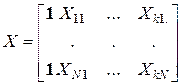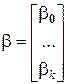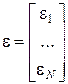Наша задача по результатам наблюдений, на основе этих наблюдений, получить надежные оценки неизвестных коэффициентов (оценить неизвестные параметры) и проверить, насколько хорошо выбранная модель соответствует исходным данным.

Каким образом получить эти оценки? Нам надо построить гиперплоскость. Из всех возможных гиперплоскостей мы хотим выбрать ту, чтобы она «наилучшим образом» подходила к нашим данным, была бы в центре скопления наших данных, т. е. чтобы все Y_i как можно ближе лежали к нашей гиперплоскости. В качестве меры близости точек к прямой мы введем разность

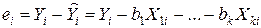
Очевидно, значения b ₁ ,…,b_k надо подбирать таким образом, чтобы минимизировать некоторую интегральную (т. е. по всем имеющимся наблюдениям) характеристику невязок или остатков:

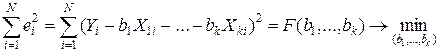
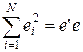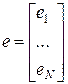, , тогда .

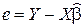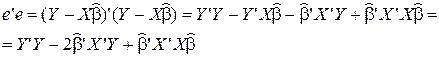
Здесь мы воспользовались тем, что 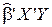- скаляр, и поэтому он совпадает со своим транспонированным значением. Необходимое условие минимума (в матричной форме):

.

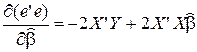Здесь мы воспользовались свойствами векторного и матричного дифференцирования:

Что значит продифференцировать вектор-функцию по вектору переменных:

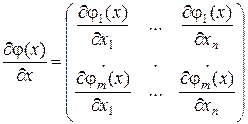
Здесь j(х) – m -мерная вектор-функция, х – n-мерный вектор.

Случаи:

1) , ,

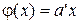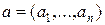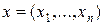
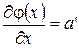
2) 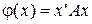, 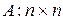- матрица

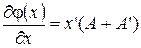, если матрица А симметричная, то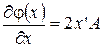

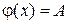
3) 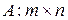- матрица.

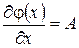
Итак,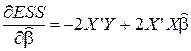

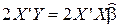
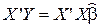, если матрица 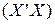невырождена, то

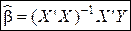- МНК оценки коэффициентов МЛРМ.

Итак, гиперплоскость мы построили. Насколько хорошо нам удалось объяснить изменение переменной Y нашей моделью. Разложим вариацию Y на две части. Насколько наше уравнение объясняет вариацию Y и какова часть Y, которую мы не можем объяснить нашим уравнением.

Рассмотрим 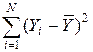- величина, являющаяся мерой вариации переменной Y вокруг ее среднего значения. Распишем эту величину:

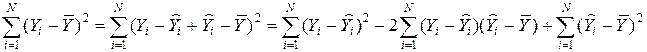I II III

В этой сумме II = 0, если в уравнении есть свободный член.

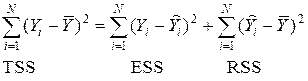
где

TSS – total sum of squares – вся дисперсия или вариация Y, характеризует степень случайного разброса значений функции регрессии около среднего значения Y;

ESS – error sum of squares – есть сумма квадратов остатков регрессии, та величина, которую мы минимизируем при построении прямой, часть дисперсии, которая нашим уравнением не объясняется;

RSS – regression sum of squares – объясненная часть дисперсии.

Определение. Коэффициентом детерминации или долей объясненной нашим уравнением дисперсии называется величина

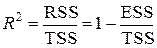
Свойства коэффициента детерминации:

1. 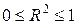в силу определения;

2. 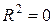- в это м случае RSS = 0, т. е. наша регрессия ничего не объясняет, ничего не дает по сравнению с тривиальным прогнозом 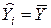. Наши данные позволяют сделать вывод о независимости Y и X, изменение в переменной X никак не влияет на изменение среднего значения переменной Y (примеры, когда зависимость между переменными есть, а коэффициент детерминации равен нулю);

3. 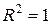- в этом случае все точки (X_i, Y_i) лежат на одной прямой (ESS = 0). Тогда на основании наших данных можно сделать вывод о наличии функциональной, а именно, линейной, зависимости между переменными Y и X. Изменение переменной Y полностью объясняется изменением переменной X;

4. 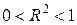- в этом случае чем ближе R ² к 1, тем лучше качество подгонки кривой к нашим данным, тем точнее 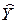аппроксимирует Y.

5. R ², вообще говоря, возрастает при добавлении еще одного регрессора, поэтому для выбора между несколькими регрессионными уравнениями не следует полагаться только на R ²

Попыткой устранить эффект, связанный с ростом R ² при увеличении числа регрессоров, является коррекция R ² на число регрессоров - наложение "штрафа" за увеличение числа независимых переменных. Скорректированный R ² - 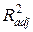: 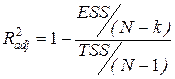(3.9)

здесь в числителе - несмещенная оценка дисперсии ошибок (как увидим позднее), в знаменателе - несмещенная оценка дисперсии Y. (Совпадают ли они?).

Свойства:

1. 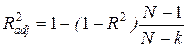- доказать самим;

2. 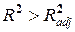, k > 1:

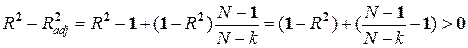, k > 1;

3. 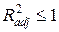, но может быть и < 0.

В определенном смысле использование 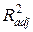для сравнении регрессий при изменении числа регрессоров более корректно.

Упражнение. Показать, что статистика 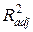увеличится при добавлении новой переменной тогда и только тогда, когда t -статистика коэффициента при этой переменной по модулю больше 1.

Следовательно, если в результате регрессии с новой переменной 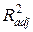увеличилась, это еще не означает, что коэффициент при этой переменной значимо отличается от нуля, поэтому мы не можем сказать, что спецификация модели улучшилась. Это первая причина, почему 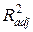не стал широко использоваться в качестве диагностической величины. Вторая причина - уменьшение внимания к самому R ². На практике даже плохо определенная модель регрессии может давать высокий коэффициент R ². Поэтому теперь он рассматривается в качестве одного из целого ряда диагностических показателей, которые должны быть проверены при построении модели регрессии. Следовательно, и корректировка его мало что дает.

Итак, при помощи регрессионного анализа мы с вами получили оценки интересующей нас зависимости (*):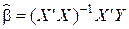

Однако, это всего лишь оценки. Возникает вопрос, насколько они хороши. Оказывается, что при выполнении некоторых условий наши оценки получаются достаточно надежными.