На практике для описания тенденции развития, следовательно, выбора типа функции, широко используются модели кривых роста. Рассмотренные выше нами функции в обобщенном виде графически представлены на рис. 7. Эти кривые могут существенно облегчить процесс выбора типа кривых:
а) полином первого порядка (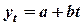 );
);
б) полином второго порядка (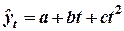 );
);
в) полином третьего порядка (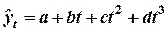 );
);
г) показательная функция (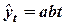 );
);
д) модифицированная экспонента (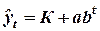 );
);
е) кривая Гомперца (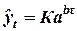 );
);
ж) логистическая кривая (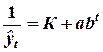 ).
).
Последнее иногда представляется следующим образом:
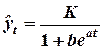 .
.
При t → -∞ ордината стремится к нулю, а при t → ∞ - к асимптоте, равной значению параметра К. Кривая симметрична относительно точки перегиба с координатами t = еnb: a; yt = K: 2.
Как видно из графика 6, логистическая функция сначала возрастает ускоренными темпами, затем темп роста замедляется и, наконец, рост почти прекращается, подтверждением является то, что кривая асимптотически приближается к некоторой прямой, параллельной оси абсцисс.

1. Полином первого порядка
(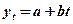 ) )
| 2. Полином второго порядка (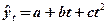 ) )
|

3. Полином третьего порядка (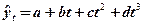 ) )
|
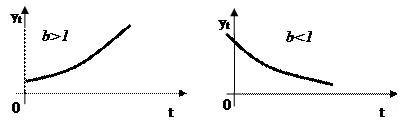
4. Показательная функция (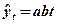 ) )
|

5. Модифицированная экспонента (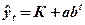 ) )
|
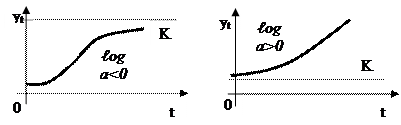
6. Кривая Гомперца (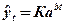 ) )
|

7. Логистическая кривая (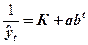 ) )
|
Рис. 6 Кривые роста
 2014-02-01
2014-02-01 739
739








