I. Краткий теоретический материал

Методические указания к выполнению работы

Четыре особых положения планеты на своей орбите относительно Земли и Солнца называются конфигурациями этой планеты. Рассмотрим конфигурации нижних (внутренних) планет – Меркурия, Венеры, и конфигурации верхних (внешних) планет – Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона. Напомним, что, если орбита планеты расположена внутри орбиты Земли, то планета называется внутренней, если орбита планеты расположена вне орбиты Земли, то планета называется внешней.

1. Для нижних планет различают следующие четыре конфигурации: нижнее соединение, западная элонгация, верхнее соединение, восточная элонгация. Рассмотрим эти конфигурации нижних планет на примере движения планеты Меркурий.

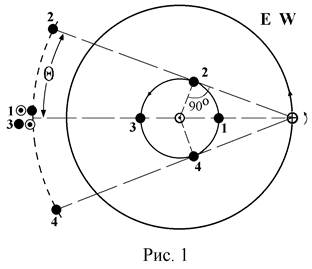
На рис. 1: ⊙ – Солнце, ⊕ – Земля на своей орбите. Стрелками указаны направления движения Земли по орбите и направление вращения Земли вокруг оси. Положение Меркурия на его орбите в моменты конфигураций обозначено как ● с индексом. Штриховая дуга – часть небесной сферы с центром в точке наблюдения на поверхности Земли. 1 ⊙●, 2 ●, 3 ●⊙, 4 ● – проекции центров дисков Солнца и Меркурия на небесную сферу в моменты конфигураций. Здесь и далее для простоты пренебрегаем наклонением орбит планет к плоскости эклиптики. Кроме того, положение Земли на рисунке фиксировано, следовательно, для Меркурия стрелкой указано направление относительного движения (оно будет совпадать с направлением действительного движения планеты по орбите).

а. В положении ● ₁ на орбите Меркурий находится между Солнцем и Землей. Для земного наблюдателя центры дисков Солнца и Меркурия “соединяются”, то есть проецируются в одну точку небесной сферы – в точку 1 ⊙●. Эклиптикальные геоцентрические долготы Меркурия и Солнца равны, то есть l_⊙ - l_● = 0°. Планета Меркурий и Солнце одновременно появляются над горизонтом в восточной стороне неба, и поэтому Меркурий нельзя будет наблюдать. Конфигурация ● ₁ – нижнее соединение. В момент нижнего соединения иногда можно наблюдать прохождение диска Меркурия (или Венеры) по диску Солнца.

б. Так как угловая скорость движения по орбите у Меркурия больше, чем у Земли, то через некоторое время Меркурий окажется в положении ● ₂, при котором угол ⊙● ₂ ⊕, то есть, угол с вершиной в центре Меркурия и со сторонами Меркурий-Солнце и Меркурий-Земля равен 90°. Центр диска Меркурия проецируется на небесную сферу в точку 2 ● и “удален” к западу (W) от проекции центра солнечного диска на некоторый угол Q – угол элонгации. Планета будет видна утром в восточной стороне неба незадолго перед восходом Солнца. Конфигурация ● ₂– западная элонгация – наибольшее западное угловое “удаление” планеты от Солнца: l_⊙ - l_● = Q.

в. После прохождения положения ● ₂диск планеты на небесной сфере будет приближаться к диску Солнца, пока Меркурий не займет на орбите положение ● ₃, при котором Солнце будет находиться между Землей и Меркурием. Центры дисков Меркурия и Солнца опять “соединятся” и будут проецироваться в одну и ту же точку небесной сферы 3 ●⊙. Как и в случае ● ₁, планета и Солнце одновременно появятся над горизонтом наблюдателя в восточной стороне неба, следовательно, Меркурий нельзя будет наблюдать: l_● - l_⊙ = 0°. Конфигурация ● ₃– верхнее соединение.

г. Продолжая свое движение по орбите, Меркурий займет положение ● ₄, при котором угол ⊙● ₄ ⊕ = 90°. Центр диска планеты будет проецироваться на небесную сферу в точку 4 ●, расположенную на угловое расстояние Q восточнее (E) центра солнечного диска, то есть l_● - l_⊙ = Q. Наблюдать планету можно вечером в западной стороне неба после захода Солнца. Утром над горизонтом Меркурий появится в лучах уже взошедшего Солнца, и наблюдать его можно только с помощью специальных инструментов. Конфигурация ● ₄– восточная элонгация – наибольшее восточное угловое “удаление” планеты от Солнца на небесной сфере.

Аналогичные конфигурации имеет и планета Венера, однако условия для наблюдений этой планеты в моменты западной и восточной элонгаций существенно лучше, чем при наблюдении Меркурия, так как. Венера “удаляется” от Солнца на небесной сфере на большее угловое расстояние. Из-за эллиптичности орбит Земли и нижних планет угловое удаление планет от центра солнечного диска в моменты элонгаций может иметь величину, лежащую в пределах: для Меркурия 17°,6¸28°,3, для Венеры 45°,0¸47°,8.

2. Для верхних планет также различают четыре конфигурации: соединение, западная квадратура, противостояние, восточная квадратура. Рассмотрим конфигурации верхних планет на примере движения по орбите планеты Марс.

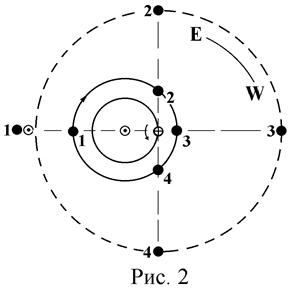На рис. 2: ⊙ – Солнце, ⊕ и ● – Земля и Марс на своих орбитах. И Земля, и Марс обращаются вокруг Солнца в прямом направлении, в направлении, совпадающем с направлением осевого вращения Земли (указано стрелкой). Положение Земли на рисунке фиксировано: для Марса стрелкой указано относительное движение – оно будет противоположно направлению действительного движения планеты. Штриховая окружность – небесная сфера с центром в точке наблюдения на поверхности Земли. 1 ●⊙, 2 ●, 3 ● и 4 ● – проекции центров дисков Солнца и Марса на небесную сферу.

а. В положении ● ₁ Марса на орбите Солнце находится между Марсом и Землей. Для наземного наблюдателя центры дисков Солнца и Марса на небесной сфере “соединяются”, то есть проецируются в одну и ту же точку небесной сферы 1 ●⊙. Эклиптикальные геоцентрические долготы Марса и Солнца равны, то есть l_⊙ - l_● = 0°. Планету наблюдать нельзя, так как Солнце и Марс восходят одновременно в восточной стороне неба. Конфигурация ● ₁ – соединение.

б. Так как угловая скорость движения Земли по орбите больше угловой скорости движения Марса, Земля будет догонять планету. Марс займет на орбите положение ● ₂. Угол ⊙⊕● ₂, то есть угол с вершиной в центре Земли и сторонами Земля- Солнце и Земля-Марс, равен 90°. Центр диска планеты проецируется на небесную сферу в точку 2 ●, расположенную на 90° западнее (W) проекции на небесную сферу центра солнечного диска: l_⊙ - l_● = 90°. Планета будет видна в восточной стороне неба всю вторую половину ночи до восхода Солнца. Конфигурация ● ₂ – западная квадратура (название “квадратура” происходит от “четверть круга”).

в. В положении ● ₃ Марса на орбите центр диска планеты проецируется в точку 3 ● небесной сферы, расположенную в 180° от проекции центра солнечного диска. Солнце и Марс находятся в противоположных точках неба, “противостоят” друг другу: l_⊙ - l_● = 180°. Планета восходит над горизонтом сразу после захода Солнца и видна всю ночь. Конфигурация ● ₃ – противостояние.

г. В положении ● ₄ Марса на орбите угол ⊙⊕● ₄ равен 90°, то есть центр диска планеты проецируется в точку 4 ● небесной сферы, расположенную на 90° к востоку (E) от проекции центра диска Солнца: l_● - l _⊙ = 90°. Марс будет виден после захода Солнца всю первую половину ночи в западной стороне неба. Конфигурация ● ₄ – восточная квадратура.

3. Промежуток времени между двумя последовательными прохождениями планетой одноименной конфигурации называется синодическим периодом S планеты.

Полный оборот планеты вокруг Солнца относительно какой-либо звезды называется сидерическим или звездным периодом Т планеты. Полный оборот Земли вокруг Солнца относительно какой-либо звезды (или какой-либо точки небесной сферы) называется сидерическим или звездным годом Т_Å. Понятно, что для Земли понятие синодического периода не имеет смысла. Из-за прецессии земной оси вращения точка весеннего равноденствия ^ движется навстречу видимому движению центра солнечного диска по небесной сфере со скоростью v» 50² в год, поэтому сидерический год Т_Å продолжительнее тропического года Т примерно на 20^m.

Т_Å = 365,257… средних солнечных суток.

Поясняя понятие “конфигурация планета”, мы фиксировали положение Земли на орбите, то есть рассматривали движение нижних и верхних планет вокруг Солнца относительно Земли. Таким образом, если сидерические периоды планет и Земли включают в себя только движение по своим орбитам, то синодический период любой планеты содержит в себе два движения: движение планеты по своей орбите и движение Земли по своей орбите. Отсюда, учитывая, что угловые скорости нижних планет больше угловой скорости движения Земли, а последняя, в свою очередь, больше угловых скоростей внешних планет, можем получить для любой планеты связь между синодическим периодом и сидерическим периодом:

1/ S _пл = 1/ T _пл - 1/ T_Å – для нижних планет (1)

1/ S _пл = 1/ T_Å - 1/ T _пл – для верхних планет (2)

Синодический период S _пл планеты и сидерический период Т_Å получаются из наблюдений, сидерический период Т _пл планеты рассчитывается по формуле (1) или (2). Уравнения (1) и (2) – уравнения синодического движения.

4. Законы Кеплера.

Первый закон Кеплера. Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых, общем для всех орбит, находится Солнце.

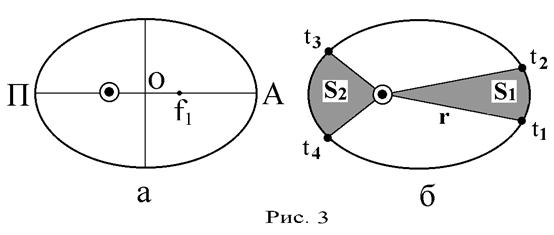На рис. 3а – эллиптическая орбита планеты: f₁и f₂ – фокусы эллиптической орбиты. Если Солнце ⊙ находится в фокусе f₂, то точка П – перигелий (наиболее близкая к Солнцу точка орбиты), а Пf₂= q – перигелийное расстояние планеты; точка А – афелий (наиболее удаленная от Солнца точка орбиты), а Аf₂= Q – афелийное расстояние планеты. За среднее расстояние а планеты от Солнца принимается большая полуось орбиты:

a = (Q + q)/2. (3)

Очевидно, что a определяет размер орбиты. Форма орбиты определяется эксцентриситетом e:

e = Of₁/OA, или e = c / a, (4)

где c – расстояние фокуса орбиты от центра эллипса.

Расстояние планеты от Солнца в перигелии и афелии равны соответственно:

q = a ×(1 – e), Q = a ×(1 + e). (5)

Второй закон Кеплера. Радиус-вектор планеты за одинаковые промежутки времени описывает равновеликие площади.

На рис. 3б изображены положения планеты на орбите в некоторые моменты времени t ₁, t ₂, t ₃ и t ₄. Солнце ⊙ расположено в одном из фокусов орбиты. Отрезок прямой, соединяющий центр Солнца с планетой на орбите, называется радиусом-вектором планеты. На рисунке ⊙ t ₁, ⊙ t ₂, ⊙ t ₃ и ⊙ t ₄– положения радиуса-вектора в соответствующие моменты времени. Из второго закона Кеплера следует, что, если промежутки времени ∆ t ₁= t ₂- t ₁и ∆ t ₂= t ₄- t ₃ равны, то равновелики площади S ₁ и S ₂, которые описывает радиус-вектор: если ∆ t ₁= ∆ t ₂, то S ₁= S ₂.

Следовательно, планета движется по орбите вокруг Солнца неравномерно. Из рис. 3б видно, что с уменьшением радиуса-вектора r планеты, то есть при приближении планеты к перигелию П, ее скорость увеличивается. И наоборот, при увеличении радиуса-вектора, то есть при приближении планеты к афелию А, ее скорость уменьшается.

Если v _к – круговая средняя скорость планеты (скорость при r = a), v _max –максимальная скорость планеты (скорость при r = q) и v _min – минимальная скорость планеты на орбите (скорость при r = Q), то справедливы соотношения:

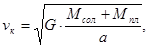
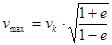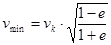, (6)

Здесь G – гравитационная постоянная, М _сол – масса Солнца, М _пл – масса планеты.

Третий закон Кеплера. Отношение квадратов сидерических периодов Т обращений планет вокруг Солнца равно отношению кубов больших полуосей а их орбит. Если Т ₁, Т ₂, а ₁ и а ₂ соответственно сидерические периоды и большие полуоси орбит двух планет, то справедливо соотношение:

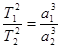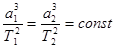, или . (7)

Соотнесем движение какой-либо планеты вокруг Солнца с движением Земли вокруг Солнца, то есть положим в формуле (7) а ₁ = а _пл, Т ₁= Т _пл, а ₂= а_Å = 1 а.е., Т ₂= Т_Å = 1 год. Тогда:

а ³_пл = Т ²_пл, (8)

причем значения а _пл и Т _пл также получим либо в астрономических единицах (для а _пл), либо в годах (для Т _пл).

5. Закон всемирного тяготения Ньютона. Любые две частицы притягиваются друг к другу с силами, величина которых прямо пропорциональна произведению масс частиц и обратно пропорциональной квадрату расстояния между ними. Силы, с которыми частицы притягивают друг друга, приложены к центрам масс частиц, расположены на прямой, соединяющей центры масс частиц, равны по величине и направлены навстречу друг другу.

Если М _⊙ – масса Солнца, М _пл – масса планеты, а –расстояние планеты от Солнца, то Солнце и планета притягивают друг друга с силой

F = G×(М _⊙× М _пл)/ а ². (9)

Ускорения, которые получают планета от Солнца w _пл и Солнце от планеты w _⊙, равны соответственно:

w _пл = G× М _⊙/ а ²×, w _⊙ = G× М _пл/ а ². (10)

Относительное ускорение w _отн при относительном круговом движении планеты по орбите вокруг Солнца вычисляется по формуле

w _отн = G×(М _⊙×+ М _пл)/ а ²_пл, или w _отн = 4p²× а _пл/ T ²_пл. (11)

Открытие Ньютоном закона всемирного тяготения позволило уточнить формулировки законов Кеплера.

Уточненный первый закон Кеплера можно сформулировать так: под действием силы тяготения небесные тела движутся вокруг центра масс по одной из кривых второго порядка – окружности, эллипсу, параболе или гиперболе.

Из (11) можно получить третий обобщенный закон Кеплера:

a ³_пл/ T ²_пл×(М _⊙×+ М _пл) = G/4p²= const. (12)

Выражения (11) и (12) справедливы для любой пары гравитирующих тел. Из (12) следует, что, если, например, мы имеем две планеты, которые движутся по орбитам вокруг Солнца, то

a ³_пл1/ T ²_пл1×(М _⊙×+ М _пл1) = a ³_пл2/ T ²_пл2×(М _⊙×+ М _пл2). (13)

Значение гравитационной постоянной G зависит от выбранной системы единиц:

в системе CGS (см., г, с): G = 6,668×10^-8×см³×г^-1×с^-2;

в системе СИ (м, кг, с): G = 6,668×10^-11×м³∙кг^-1×с^-2;

в гауссовой или астрономической системе (а.е., М _⊙, ср. солн. сутки):G = K²= 2,959×10^-4, где K = 1,7202×10^-2 – гауссова постоянная.

Если нам известна круговая скорость v _к, то значение параболической скорости v _п можно получить по формуле:

v _п = v _к×2^1/2 =.1,414× v _к. (14)

Если R _пл – радиус планеты, то ускорение силы тяжести g на поверхности планеты равно:

g = G× М _пл/ R ²_пл. (15)

Критическая скорость v _кр, при которой тело массой m << М _пл покидает планету и удаляется от нее по параболе, связана с ускорением силы тяжести g соотношением:

v _кр = (2g× R _пл)^1/2. (16)

II. Методика решения задач по теме “Движение планет. Законы Кеплера”

Методику решения задач по теме “Движение планет. Законы Кеплера” продемонстрируем на решении типовых задач.

Задача 1. Определить промежуток времени между двумя последовательными противостояниями планеты Плутон, если сидерический период планеты Т _Плут равен 248,6 лет.

Решение: Дано: Т _Плут= 248,6 лет. Требуется найти S _Плут.

Так как Плутон – верхняя планета, то для решения задачи используем формулу (2). Принимая T_Å = 1 год, получим:

S _Плут = Т _Плут× T_Å /(Т _Плут - T_Å) = 248,6×1/(248,6 - 1) = 1,004 г.

Ответ: S _Плут = 1,004 года.

Задача 2. Определить наименьшую и наибольшую элонгации планеты Меркурий, если большая полуось орбиты Меркурия 0,387 а.е., эксцентриситет орбиты 0,2066, большая полуось орбиты Земли 1а.е., эксцентриситет орбиты Земли 0,0167.

Решение: Дано: а _Мер = 0,387 а.е., е _Мер= 0,2066, а_Å = 1 а.е., е_Å = 0,0167. Найти: Θ _Мер,_max, Θ _Мер,_min.

Из рис. 1 видно, что элонгация Меркурия будет наименьшей тогда, когда в момент элонгации Меркурий будет в перигелии, а Земля в афелии. Воспользовавшись формулами (5), запишем:

q _Мер= a _Мер×(1 - e _Мер); Q_Å = а_Å ×(1 + е_Å);

Из треугольника ⊙● ₂ Å:

sin Θ _Мер,_min = (⊙● ₂)/(⊙Å) = a _Мер×(1 - e _Мер)/ а_Å ×(1 + е_Å) = 0,387×(1 - 0,2066)/1×(1 + 0,0167) = 0,3070/1,0167= 0,3020;

Θ _Мер,_min = 17°,6.

Элонгация Меркурия будет наибольшей тогда, когда в момент элонгации Меркурий будет в афелии, а Земля в перигелии.

Θ _Мер,_max= a _Мер×(1 + e _Мер); q_Å = а_Å ×(1 - е_Å);

Из треугольника ⊙● ₂ Å:

sin Θ _Мер,_max = a _Мер×(1 + e _Мер)/ а_Å ×(1 - е_Å) = 0,387×(1 + 0,2066)/1×(1 - 0,0167) = 0,4670/0,9833 = 0,4749;

Θ _Мер,_max = 28°,3.

Ответ: Θ _Мер,_min = 17°,6, Θ _Мер,_max = 28°,3.

Задача 3. Определить наименьшее и наибольшее расстояния между Землей и Плутоном, если большая полуось земной орбиты 1 а.е., эксцентриситет земной орбиты 0,0167, большая полуось орбиты Плутона 39,44 а.е., эксцентриситет орбиты Плутона 0,247.

Решение: Дано: а_Å = 1 а.е., е_Å = 0,0167, a _Плут = 39,48 а.е., e _Плут = 0,249. Требуется определить Δ_Плут,min, Δ_Плут,max.

Из рис. 2 видно, что расстояние между Землей и Плутоном будет минимальным тогда, когда Земля будет находиться в афелии, а Плутон в перигелии и противостоянии. Учитывая формулы (5), можем записать:

Δ_Плут,min= q _Плут- Q_Å = a _Плут×(1 - e _Плут) - a_Å ×(1 + e_Å),

Δ_Плут,min= 39,48×0,751 - 1×1,0167 = 28,63 а.е.

Расстояние между Землей и Плутоном будет максимальным тогда, когда Земля будет находиться в афелии, а Плутон в афелии и соединении.

Δ_Плут,max= Q _Плут+ Q_Å = a _Плут×(1 + e _Плут) + a_Å ×(1 + e_Å),

Δ_Плут,max= 39,48×1,249 + 1×1,0167 = 50,33 а.е.

Ответ: Δ_Плут,min= 28,63 а.е., Δ_Плут,max= 50,33 а.е.

Задача 4. Круговая скорость движения Земли по орбите 29,78 км/с. Найти минимальную и максимальную скорости движения Земли по орбите, если эксцентриситет орбиты Земли 0,0167.

Решение: Дано: v_Å _к= 29,78 км/с, e_Å = 0,0167. Найти v_Å _min, v_Å _max.

Воспользуемся формулами (6):

v_Å _min = v_Å _к×[(1 - e_Å)/(1 + e_Å)]^1/2 = 29,78×0,9834 = 29,29 км/с;

v_Å _max = v_Å _к×[(1 + e_Å)/(1 - e_Å)]^1/2 = 29,78×1,0168 = 30,28 км/с;

Ответ: v_Å _min = 29,29 км/с, v_Å _max = 30,28 км/с.

Задача 5. Максимальное расстояние планеты Меркурий от Солнца 0,467 а.е. Чему равен сидерический период планеты, если эксцентриситет орбиты Меркурия 0,2066.

Решение: Дано: Q _Мерк= 0,467 а.е., е _Мерк= 0,2066. Найти Т _Мерк.

Для решения воспользуемся соотношениями (5) и (8):

Q _Мерк = a _Мерк×(1 + e _Мерк);

a _Мерк = Q _Меркк/(1 + e _Мерк) = 0,467/1,2066 = 0,387 а.е;

Т _Мерк = (a_Мерк)^3/2 = 0,24 года.

Ответ: Т _Мерк = 0,24 года = 87,9 ср. солн. cуток.

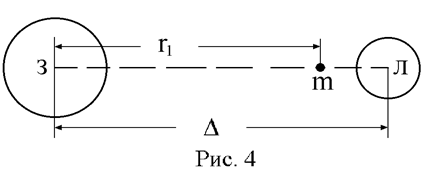
Задача 6. Расстояние между центрами Земли и Луны равно 60× R_Å. Отношение масс Земли и Луны равно 81:1. В какой точке прямой, проведенной между центрами планет, какое-либо тело m будет притягиваться Землей и Луной с одинаковой силой?

Решение:

Дано: Δ = 60×R _Å, M_Å / M _Лун = 81/1. Найти r ₁. (см. рис. 4)

Воспользуемся для решения формулой (15):

Ускорение, которое получает тело m от притяжения Землей:

g ₁ = G× M_Å / r ₁²,

Ускорение, которое получает тело m от притяжения Луной:

g₂ = G× M _Лун/(Δ - r ₁)², = G× M _Лун/(60×R _Å - r ₁)².

В искомой точке эти ускорения равны, то есть g ₁ = g ₂.

G× M_Å / r ₁² = G× M _Лун/(60×R _Å - r ₁)²,

M_Å / M _Лун= r ₁²/(60×R _Å - r ₁)²,

81 = r ₁²/(60×R _Å - r ₁)²,

9 = r ₁/(60×R _Å - r ₁), 9×(60×R _Å - r ₁) = r ₁,

540×R _Å = 10× r ₁, r ₁ = 54×R _Å.

Ответ: Искомое расстояние равно 54×R _Å от центра Земли.

Задача 7. Среднее расстояние спутника Марса Фобоса 9,4×10³ км. Сидерический период обращения Фобоса 0,3189 суток. Найти массу планеты Марс в массах Земли. Воспользоваться данными о системе Земля-Луна.

Решение: Дано: а _Фоб= 9,4×10³ км, Т _Фоб= 0,3189 сут., а _Лун= 3,844×10⁵ км, Т _Лун= 27,3117 сут., М_Å / M _Лун = 81,3. Найти М _Марс в М _Å.