Метод экстраполяции по среднему темпу роста
Метод экстраполяции по среднему абсолютному приросту
Математические методы демографического прогнозирования
А. Методы экстраполяции – простейшие методы прогнозирования, основанные на предположении неизменности среднегодовых темпов роста, среднегодовых абсолютных и относительных приростов.
Методы экстраполяции применяются в демографии для расчёта общей численности населения только при отсутствии резких колебаний рождаемости, смертности и миграции.
Математическая модель по этому методу имеет вид линейной функции:
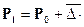 t, (7.1)
t, (7.1)
где 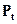 – прогнозируемый уровень численности населения;
– прогнозируемый уровень численности населения;
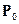 – базовый уровень численности населения;
– базовый уровень численности населения;
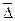 – абсолютный среднегодовой прирост численности населения;
– абсолютный среднегодовой прирост численности населения;
t – период прогнозирования.
В реальности неизменные среднегодовые абсолютные приросты могут оставаться таковыми только непродолжительное время, поэтому прогнозирование численности населения с использованием указанной линейной функции может быть использовано только в краткосрочных прогнозах.
Математическая модель по этому методу имеет вид степенной функции:
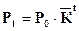 , (7.2)
, (7.2)
где: 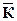 – среднегодовой коэффициент роста численности населения.
– среднегодовой коэффициент роста численности населения.
В этой модели предполагается ежегодное изменение численности населения в одно и то же число раз, т.е. его рост (или снижение) в геометрической прогрессии.
От среднегодовых коэффициентов роста можно перейти к среднегодовым коэффициентам прироста, и тогда формулу (7.2) можно преобразовать следующим образом:
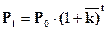 , (7.3)
, (7.3)
где 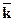 – среднегодовой коэффициент прироста населения.
– среднегодовой коэффициент прироста населения.
Путём преобразования формулы (7.3) можно определить период удвоения населения:
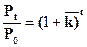 (7.4)
(7.4)
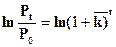 (7.5)
(7.5)
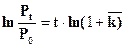 (7.6)
(7.6)
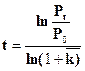 (7.7)
(7.7)
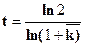 (7.8)
(7.8)
Соответственно, период сокращения населения вдвое будет определяться по следующей формуле:
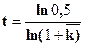 (7.9)
(7.9)
Задание 7.1. Известно, что коэффициент естественного прироста в населении Средней Азии составил 10%о (данные условные).
Требуется определить число лет, через которое численность населения увеличится в 2 раза при условии сохранения темпа роста и отсутствия миграции.
Решение:
Определим период удвоения населения данного региона, используя формулу 7.8:
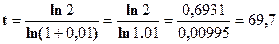 (лет).
(лет).
Математическая модель по этому методу имеет вид экспоненциальной функции:
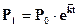 , (7.10)
, (7.10)
где: e – основание натурального логарифма (2,7183);
Применение экспоненциальной функции более предпочтительно по сравнению с линейной функцией и степенной, т.к. это гарантирует, что численность населения не станет отрицательной.
Используя этот метод, можно рассчитать период удвоения численности населения и среднегодовой коэффициент прироста населения.
Период удвоениянаселения получаем путём следующих преобразований исходной формулы (7.10):
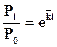 , (7.11)
, (7.11)
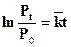 (7.12)
(7.12)
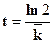 (7.13)
(7.13)
Соответственно, период сокращения населения вдвое будет тогда рассчитываться по следующей формуле:
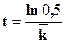 (7.14)
(7.14)
Задание 7.2. Известно, что население одного из регионов России имеет среднегодовой темп сокращения, равный 1,41% (данные условные).
Требуется определить число лет, через которое постоянное население уменьшится в 2 раза.
Решение:
Период сокращения населения вдвое рассчитаем по формуле 7.14:
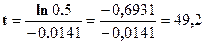 (лет).
(лет).
Среднегодовой коэффициент прироста населения можно определить путём преобразований промежуточной формулы расчёта (7.12):
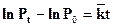 (7.15)
(7.15)
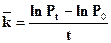 (7.16)
(7.16)
Б. Аналитический метод – основан на подборе функции, наиболее близкой по своему графическому отображению к эмпирической кривой.
 2013-12-31
2013-12-31 1086
1086
