Лекция 8. Проверка статистических гипотез
8.1. Статистические гипотезы и критерии
8.2. Т – критерий
8.3. F – критерий
8.4. Критерий согласия Пирсона
8.1. Статистические гипотезы и критерии
Пусть имеется некоторая генеральная совокупность, порождённая функцией распределения F (x) случайной величины Х. Каждое высказывание или всякое множество непротиворечивых предположений относительно параметров генеральной совокупности (M (Х), D (X) и т.д.) или вида функции распределения F (x), будем называть статистической гипотезой и обозначать Но. В качестве примеров можно привести такие гипотезы: 1) М (Х) = 2,2; 2) D (X) < 10; 3) Х Î N (-1; 4); 4) X равномерно распределена на отрезке [-1; 3]; 5) Гxy = 0; 6) M (X) = M (Y); 7) M (X) - M (Y) < 0; 8) D (X) = D (Y); 9) F 1(x) = F 2(x), где F 1(x), F 2(x) - функции распределения случайных величин X и Y.
Поставим следующую задачу. На основании имеющейся выборки 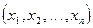 или двух выборок
или двух выборок 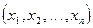 и
и 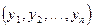 из разных генеральных совокупностей проверить гипотезу Но, т.е. принять одно из двух решений: гипотеза Но принимается или отвергается. Правило, по которому принимается или отклоняется данная гипотеза, называется статистическим критерием.
из разных генеральных совокупностей проверить гипотезу Но, т.е. принять одно из двух решений: гипотеза Но принимается или отвергается. Правило, по которому принимается или отклоняется данная гипотеза, называется статистическим критерием.
Для проверки гипотезы Но подбирается контрольная величина j, являющаяся функцией от результатов наблюдений: 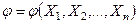 или
или 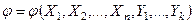 . Такая, соответствующим образом выбранная и приспособленная к решаемой задаче, выборочная функция называется статистикой критерия. Последняя должна удовлетворять следующим условиям.
. Такая, соответствующим образом выбранная и приспособленная к решаемой задаче, выборочная функция называется статистикой критерия. Последняя должна удовлетворять следующим условиям.
1. При выполнении гипотезы Но статистика j, должна подчиняться известному (табулированному) закону распределения.
2. Значение статистики 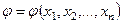 или
или 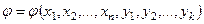 должно быть мерой “расхождения выборки и гипотезы Но ”.
должно быть мерой “расхождения выборки и гипотезы Но ”.
Проверка статистической гипотезы Но сводится к следующему.
По заданному уровню значимости a (обычно a = 0,05; a = 0,01, a = 0,001) отыскивается такая критическая область Акр, что условная вероятность попадания в неё статистики j при условии справедливости гипотезы Но меньше a:
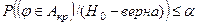 . (8.1)
. (8.1)
Область Акр всегда можно найти, если известно распределения статистики j или хотя бы её асимптотическое распределение, т.е. распределение для больших объемов выборки.
Если реализовавшееся значение статистики jэмп попало в область Акр (это событие, имеющее маленькую вероятность a), то от гипотезы Но отказываются.
Если же jэмп не попало в область Акр, то говорят, что данные наблюдений не противоречат гипотезе Но на уровне значимости a.
Если гипотеза Но отвергается, хотя она на самом деле верна, то говорят, что совершена ошибка первого рода.
Заметим, что уровень значимости a есть вероятность ошибки первого рода, т.к. 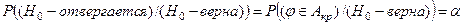 .
.
Если гипотеза Но принимается, хотя она в действительности неверна, то говорят, что совершена ошибка второго рода. Вероятность ошибки второго рода обозначают b, т.е. 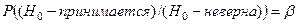 .
.
Если уровень значимости a задан, то критическую область Акр, определяемую по формуле (8.1), можно найти многими способами. Принято так определять Акр, чтобы вероятность ошибки второго рода была наименьшей. Критические области, которые будут в дальнейшем построены, будут выбираться именно по этому критерию.
Итак, перечислим основные этапы процедуры проверки статистической гипотезы.
1. Исходя из условий рассматриваемой задачи и располагая выборкой 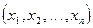 или выборками
или выборками 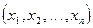 ;
; 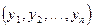 , формулируют основную или нулевую гипотезу Но и альтернативную гипотезу Н1, которая конкурирует с Но.
, формулируют основную или нулевую гипотезу Но и альтернативную гипотезу Н1, которая конкурирует с Но.
Конкуренция гипотез Но и Н1 означает, что события (Но - верна) и (Н1 - верна) являются дополнительными или как иногда говорят, противоположными, т.е. процедура проверки статистической гипотезы заканчивается принятием решения: Но - верна или Н1 - верна.
2. Задавшись уровнем значимости a и выбрав критерий 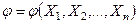 или
или 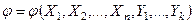 , определяют критическую область Акр из условия
, определяют критическую область Акр из условия 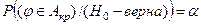 .
.
В зависимости от вида основной Но и альтернативной Н1 гипотез и распределения критерия j возможны три вида критической области Акр:
а) 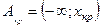 - левосторонняя критическая область, а значение хкр определяется из уравнения
- левосторонняя критическая область, а значение хкр определяется из уравнения 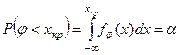 , где
, где 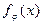 - плотность вероятности статистики j;
- плотность вероятности статистики j;
б) 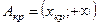 - правосторонняя критическая область, а значение хкр определяется из уравнения
- правосторонняя критическая область, а значение хкр определяется из уравнения 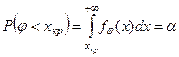 ;
;
в) 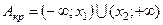 - двусторонняя критическая область, а величины х1 и х2 определяются из уравнений
- двусторонняя критическая область, а величины х1 и х2 определяются из уравнений
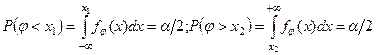 .
.
3. Используя данные выборки 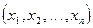 или выборок
или выборок 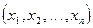 ;
;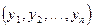 вычисляют значение критерия
вычисляют значение критерия 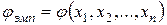 или
или 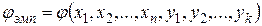 . И если j эмп Î Акр, то принимается гипотеза Н1, а если j эмп Ï Акр, то гипотеза Но.
. И если j эмп Î Акр, то принимается гипотеза Н1, а если j эмп Ï Акр, то гипотеза Но.
Итак, если jэмп Ï Акр, то Но принимается, но это не означает, что Но является единственно подходящей гипотезой, а просто говорит о том, что расхождение между данными выборки и гипотезой Но мало, или другими словами, что гипотеза Но не противоречит результатам наблюдений. Но наряду с Но таким же свойством могут обладать и другие гипотезы.
Если jэмп . Î Акр, то гипотеза Но отвергается и принимается альтернативная гипотеза Н1, хотя при этом можно и допустить ошибку с вероятностью a.
П р и м е р № 1. Из генеральной совокупности, имеющей распределение 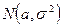 , произведена выборка объема n = 100. Реализовавшиеся значения функций выборок (статистик)
, произведена выборка объема n = 100. Реализовавшиеся значения функций выборок (статистик) 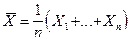 и
и 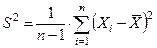 равны
равны 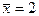 и
и 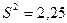 .
.
На уровне значимости a = 0,05 проверить статистическую гипотезу Но: а = 1 при наличии альтернативных гипотез Н1: 1) Н1: а ¹ 1; 2) Н1: а > 1;3) Н1: а < 1.
Р е ш е н и е.
1. Рассматриваются основная гипотеза Но: а = 1 и альтернативная Н1: а ¹ 1.
В качестве критерия выбираем статистику 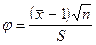 , случайная величина j имеет распределение Стьюдента с m = n - 1 = 99 степенями свободы. Для уровня значимости a = 0,05 и m = 99 найдем такое хкр > 0, чтобы
, случайная величина j имеет распределение Стьюдента с m = n - 1 = 99 степенями свободы. Для уровня значимости a = 0,05 и m = 99 найдем такое хкр > 0, чтобы 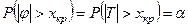 , где Т - случайная величина, имеющая распределение Стьюдента с m = 99 степенями свободы.
, где Т - случайная величина, имеющая распределение Стьюдента с m = 99 степенями свободы.
По табл. 4 Приложения находим корень уравнения 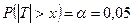 : хкр » 1,99. Поэтому в рассматриваемом случае критическая область Акр имеет вид: (-¥; -1,99) È (1,99; +¥).
: хкр » 1,99. Поэтому в рассматриваемом случае критическая область Акр имеет вид: (-¥; -1,99) È (1,99; +¥).
Вычислим значение критерия по данным выборки 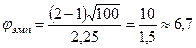 . Как видим, jэмп Î Акр, и поэтому принимается гипотеза Н1: а = М (Х) ¹ 1.
. Как видим, jэмп Î Акр, и поэтому принимается гипотеза Н1: а = М (Х) ¹ 1.
2. Рассмотрим основную гипотезу Но: а =1 и альтернативную Н1: а > 1.
Критерий остается прежним: 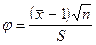 , однако критическая область в данном случае будет правой односторонней
, однако критическая область в данном случае будет правой односторонней 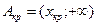 . Величина хкр есть корень уравнения
. Величина хкр есть корень уравнения 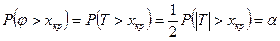 . С помощью табл. 4 находим корень уравнения
. С помощью табл. 4 находим корень уравнения 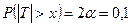 для m = 99:
для m = 99: 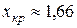 . Следовательно, критическая область в этом случае: (1,66; +¥). Т.к. jэмп = 6,7 Î Акр, то принимается гипотеза: а > 1.
. Следовательно, критическая область в этом случае: (1,66; +¥). Т.к. jэмп = 6,7 Î Акр, то принимается гипотеза: а > 1.
3. Рассмотрим основную гипотезу Но: а =1 и альтернативную Н1: а < 1. Критерий прежний: 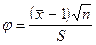 , а критическая область Акр - левая односторонняя: (-¥; хкр), где хкр < 0.
, а критическая область Акр - левая односторонняя: (-¥; хкр), где хкр < 0.
Величина хкр есть корень уравнения
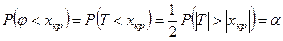 , т.е.
, т.е. 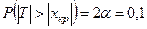 .
.
По табл. 4 Приложения находим корень уравнения 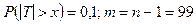 :
: 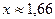 . Приравняв хкр = - х, получаем
. Приравняв хкр = - х, получаем 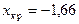 . Итак,
. Итак, 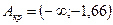 , и т.к. j эмп = 6,7 Ï Акр, то принимается основная гипотеза Но (а = 1) и отвергается конкурирующая гипотеза Н1 (а > 1).
, и т.к. j эмп = 6,7 Ï Акр, то принимается основная гипотеза Но (а = 1) и отвергается конкурирующая гипотеза Н1 (а > 1).
Подведем итоги. Проверка статистической гипотезы Но: а = 1, проведённая в п. 1, показала, что а ¹ 1. Результаты, полученные в п. 3, дали основание считать неверной гипотезу Н1: а < 1. В п. 2 установлено, что а > 1 с вероятностью 1- a = 0,95.
П р и м е р № 2. Из генеральной совокупности, имеющей распределение 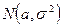 , произведена выборка объемом n = 26. Вычисленное по выборке значение статистики
, произведена выборка объемом n = 26. Вычисленное по выборке значение статистики 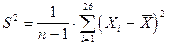 оказалось равным S 2 = 30.
оказалось равным S 2 = 30.
Рассматриваются основная 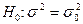 и альтернативная
и альтернативная 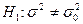 гипотезы. Каким должен быть параметр
гипотезы. Каким должен быть параметр 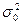 , чтобы на уровне значимости a = 0,1 оказалась верной основная гипотеза Но?
, чтобы на уровне значимости a = 0,1 оказалась верной основная гипотеза Но?
Р е ш е н и е. В качестве критерия выберем статистику 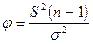 , которая в случае справедливости гипотезы Но имеет вид
, которая в случае справедливости гипотезы Но имеет вид 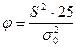 . Случайная величина j имеет хи-квадрат распределение с m = n - 1 = 25 степенями свободы. Критическая область, соответствующая основной
. Случайная величина j имеет хи-квадрат распределение с m = n - 1 = 25 степенями свободы. Критическая область, соответствующая основной 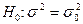 и альтернативной гипотезам
и альтернативной гипотезам 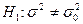 имеет вид
имеет вид 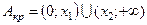 , где величины х1 и х2 удовлетворяют уравнениям:
, где величины х1 и х2 удовлетворяют уравнениям:
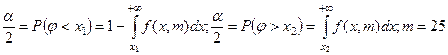 .
.
Решая с помощью табл. 5 Приложения уравнения: 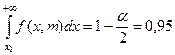 и
и 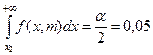 , получим
, получим 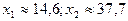 . Значит, критическая область такова:
. Значит, критическая область такова: 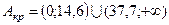 .
.
Значение вычисленного по выборке критерия равно 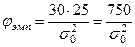 . Чтобы оказалась верной гипотеза Но на уровне значимости a = 0,1, должно выполниться условие jэмп Ï Акр, т.е. 14,6 £ j эмп. £ 37,7 или
. Чтобы оказалась верной гипотеза Но на уровне значимости a = 0,1, должно выполниться условие jэмп Ï Акр, т.е. 14,6 £ j эмп. £ 37,7 или 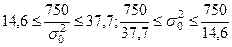 . Окончательно получаем ответ на поставленный вопрос: значение дисперсии должно лежать в диапазоне
. Окончательно получаем ответ на поставленный вопрос: значение дисперсии должно лежать в диапазоне 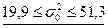 .
.
П р и м е р № 3. Дана парная выборка объема n = 52: 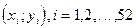 . Известно, что в генеральной совокупности случайные величины Х и Y распределены нормально, а их коэффициент корреляции равен
. Известно, что в генеральной совокупности случайные величины Х и Y распределены нормально, а их коэффициент корреляции равен 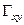 . По выборке получено значение коэффициента корреляции
. По выборке получено значение коэффициента корреляции 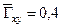 . На уровне значимости a = 0,05 проверить статистическую гипотезу:
. На уровне значимости a = 0,05 проверить статистическую гипотезу: 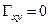 .
.
Р е ш е н и е. Основная гипотеза 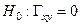 , а альтернативная -
, а альтернативная - 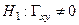 . В качестве критерия выбираем статистику
. В качестве критерия выбираем статистику 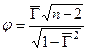 , которая в случае справедливости основной гипотезы Но имеет распределение Стьюдента с m = = n - 2 = 50 степенями свободы. Критическая область имеет вид:
, которая в случае справедливости основной гипотезы Но имеет распределение Стьюдента с m = = n - 2 = 50 степенями свободы. Критическая область имеет вид: 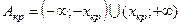 , где хкр является корнем уравнения
, где хкр является корнем уравнения 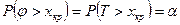 . Решая с помощью табл. 4 Приложения уравнение
. Решая с помощью табл. 4 Приложения уравнение 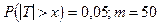 , получаем
, получаем 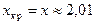 . Итак,
. Итак, 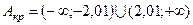 .
.
Значение критерия, вычисленное по данным выборки, равно 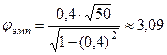 . Т.к. jэмп Î Акр, то основная гипотеза
. Т.к. jэмп Î Акр, то основная гипотеза 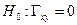 отвергается, а альтернативная гипотеза
отвергается, а альтернативная гипотеза 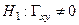 принимается.
принимается.
В качестве альтернативной было бы разумно рассмотреть гипотезу 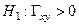 , ибо
, ибо 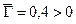 . В этом случае
. В этом случае 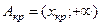 , где хкр есть корень уравнения
, где хкр есть корень уравнения 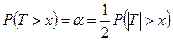 . С помощью табл. 4, для числа степеней свободы m = n - 2 = 50 находим корень уравнения
. С помощью табл. 4, для числа степеней свободы m = n - 2 = 50 находим корень уравнения 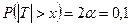 :
: 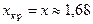 . Итак,
. Итак, 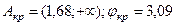 , и т.к. jэмп Î Акр, то принимается гипотеза
, и т.к. jэмп Î Акр, то принимается гипотеза 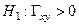 .
.
8.2. Т – критерий
Т - критерий служит для сравнения математических ожиданий двух генеральных совокупностей аx и аy, порождённых нормальными распределениями с неизвестными, но одинаковыми дисперсиями.
Пусть 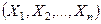 и
и 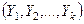 - независимые математические выборки из первой и второй генеральной совокупностей. Проверяется основная гипотеза
- независимые математические выборки из первой и второй генеральной совокупностей. Проверяется основная гипотеза 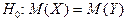 , т.е.
, т.е. 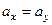 . В случае справедливости гипотезы Но статистика
. В случае справедливости гипотезы Но статистика 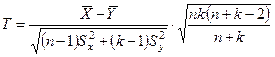
имеет распределение Стьюдента с m = n + k - 2 степенями свободы. Здесь,
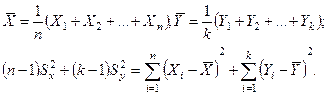
Этот факт позволяет построить критерий для проверки гипотезы Но.
В качестве критерия выбирается статистика j = Т.
1. Если альтернативная гипотеза 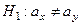 , то критическая область имеет вид
, то критическая область имеет вид 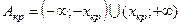 , где величина хкр > 0 является корнем уравнения
, где величина хкр > 0 является корнем уравнения 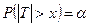 , где a - заданный уровень значимости, m = n + k - 2 - число степеней свободы распределения Стьюдента. Уравнение решается с помощью табл. 4 Приложения.
, где a - заданный уровень значимости, m = n + k - 2 - число степеней свободы распределения Стьюдента. Уравнение решается с помощью табл. 4 Приложения.
По данным выборок 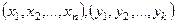 вычисляются значения
вычисляются значения 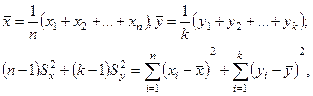
после чего определяется значение критерия
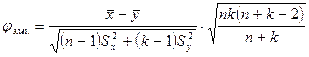 .
.
Если jэмп Î Акр, то принимается альтернативная гипотеза 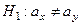 , а если j эмп Ï Акр, то принимается основная гипотеза
, а если j эмп Ï Акр, то принимается основная гипотеза 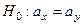 .
.
2. Если альтернативная гипотеза 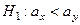 , т.е.
, т.е. 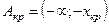 , где хкр > 0 есть корень уравнения
, где хкр > 0 есть корень уравнения 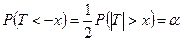 , т.е.
, т.е. 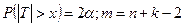 . Этот корень находится по табл. 4 Приложения. Затем вычисляется jэмп ., и если jэмп Î Акр, то принимается гипотеза
. Этот корень находится по табл. 4 Приложения. Затем вычисляется jэмп ., и если jэмп Î Акр, то принимается гипотеза 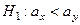 , а если jэмп Ï Акр, то принимается основная гипотеза
, а если jэмп Ï Акр, то принимается основная гипотеза 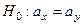 .
.
3. Если альтернативная гипотеза 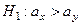 , то критическая область имеет вид
, то критическая область имеет вид 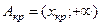 , где величина хкр > 0 есть корень уравнения
, где величина хкр > 0 есть корень уравнения 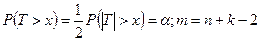 . По табл. 4 определяется хкр, вычисляется jэмп ., и если, jэмп Î Акр, то принимается альтернативная гипотеза
. По табл. 4 определяется хкр, вычисляется jэмп ., и если, jэмп Î Акр, то принимается альтернативная гипотеза 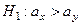 , а если jэмп Ï Акр, то принимается основная гипотеза
, а если jэмп Ï Акр, то принимается основная гипотеза 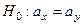 .
.
П р и м е р. После обработки втулок на станке-автомате в понедельник и пятницу было отобрано две пробы по десять деталей в каждой. Были измерены диаметры этих втулок с точностью до тысячных долей сантиметра. Результаты измерения (в см) диаметров этих втулок приводятся в таблице:
| № детали | |||||
| Проба 1 | 2,066 | 2,063 | 2,068 | 2,060 | 2,067 |
| Проба 2 | 2,063 | 2,060 | 2,057 | 2,056 | 2,059 |
| 2,063 | 2,059 | 2,062 | 2,062 | 2,060 |
| 2,058 | 2,062 | 2,059 | 2,059 | 2,057 |
Распределение диаметров предполагается нормальным, и поскольку выборки извлечены из продукции, произведенной одним станком, то можно считать дисперсии обоих выборок равными.
Проверить на уровне значимости a = 0,01 гипотезу о том, что математические ожидания генеральных совокупностей деталей, произведенных в понедельник и пятницу, равны. Другими словами, надо проверить, что режим работы станка-автомата с понедельника до пятницы не изменился.
Р е ш е н и е. За основную гипотезу принимаем 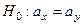 , а за альтернативную -
, а за альтернативную -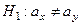 . В качестве критерия выбираем статистику
. В качестве критерия выбираем статистику
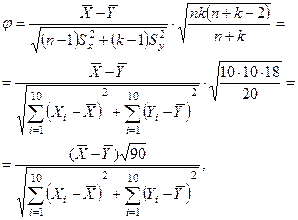
имеющую распределение Стьюдента с m = 10 + 10 - 2 = 18 степенями свободы. Критическая область имеет вид 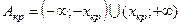 , где хкр есть корень уравнения
, где хкр есть корень уравнения 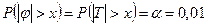 . По табл. 4 Приложения для a = 0,01 и m = 18 находим
. По табл. 4 Приложения для a = 0,01 и m = 18 находим 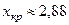 . Поэтому
. Поэтому 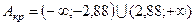 .
.
Вычислим эмпирическое значение критерия j, для чего посчитаем входящие туда величины.
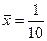 × (2,066 + 2,063 + 2,068 + 2,060 + 2,067 + 2,063 + 2,059 + 2,062 + 2,062
× (2,066 + 2,063 + 2,068 + 2,060 + 2,067 + 2,063 + 2,059 + 2,062 + 2,062
+ 2,060) = 2,063;
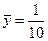 × (2,063 + 2,060 + 2,057 + 2,056 + 2,059 + 2,058 + 2,062 + 2,059 + 2,059+ +2,057) = 2,059;
× (2,063 + 2,060 + 2,057 + 2,056 + 2,059 + 2,058 + 2,062 + 2,059 + 2,059+ +2,057) = 2,059;
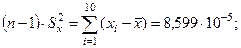
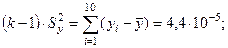
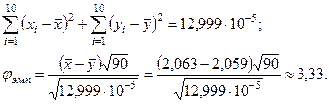
Поскольку j Î Акр, то принимается альтернативная гипотеза 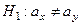 , т.е. режим работы станка-автомата c понедельника до пятницы изменился.
, т.е. режим работы станка-автомата c понедельника до пятницы изменился.
З а м е ч а н и я.
1. По отношению к требованию нормального распределения генеральной совокупности Т - критерий не очень чувствительный. Его можно применять, если статистическое распределение обеих выборок (т.е. их гистограммы) имеют по одной вершине и приблизительно симметричны относительно своих мод.
2. Требование 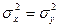 часто может быть обосновано на содержательном уровне, при этом гипотезу
часто может быть обосновано на содержательном уровне, при этом гипотезу 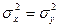 можно проверить по F - критерию.
можно проверить по F - критерию.
8.3. F – критерий
Гипотезы о дисперсиях имеют в технике большое значение, так как 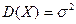 есть числовая мера таких характеристик, как точность обработки изделия, ошибки измерительных приборов, точность технологических процессов и т. п. При этом часто требуется сравнить дисперсии различных математических выборок. Для проверки гипотезы
есть числовая мера таких характеристик, как точность обработки изделия, ошибки измерительных приборов, точность технологических процессов и т. п. При этом часто требуется сравнить дисперсии различных математических выборок. Для проверки гипотезы 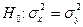 или
или 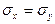 строится F - критерий. Дело в том, что при справедливости гипотезы Но случайная величина
строится F - критерий. Дело в том, что при справедливости гипотезы Но случайная величина 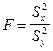 , равная отношению исправленных выборочных дисперсий, соответствующих независимым математическим выборкам из генеральных совокупностей распределений
, равная отношению исправленных выборочных дисперсий, соответствующих независимым математическим выборкам из генеральных совокупностей распределений 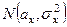 и
и 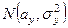 , имеет так называемое F - распределение с (m, l) степенями свободы, где m = n - 1; l = k - 1, а числа n и k - объемы выборок
, имеет так называемое F - распределение с (m, l) степенями свободы, где m = n - 1; l = k - 1, а числа n и k - объемы выборок 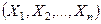 и
и 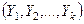 . В качестве одной из трех возможных альтернативных гипотез берут: а)
. В качестве одной из трех возможных альтернативных гипотез берут: а)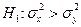 ; б)
; б)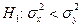 ; в)
; в)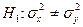 .
.
В табл. 6 Приложения F - распределение приводятся для двух значений параметра a: a = 0,05 и a = 0,01 (a - уровень значимости), причем считается, что 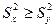 , т.е. рассматривается случай, когда
, т.е. рассматривается случай, когда 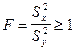 . По этой таблице можно найти решение уравнения
. По этой таблице можно найти решение уравнения 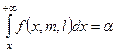 , где
, где 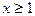 ,
, 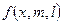 - плотность вероятности F - распределения с m и l степенями свободы.
- плотность вероятности F - распределения с m и l степенями свободы.
Рассмотрим три задачи, соответствующие трём различным альтернативным гипотезам.
1. Проверка основной гипотезы 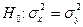 при наличии альтернативной
при наличии альтернативной
гипотезы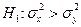 на уровне значимости a сводится к построению критической области
на уровне значимости a сводится к построению критической области 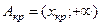 , где хкр есть корень уравнения
, где хкр есть корень уравнения 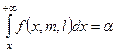 , и вычислению значения статистики
, и вычислению значения статистики 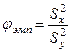 , где
, где 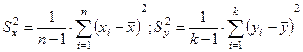 - это значения исправленных выборочных дисперсий, вычисленные по имеющимся выборкам
- это значения исправленных выборочных дисперсий, вычисленные по имеющимся выборкам 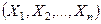 и
и 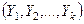 . Если jэмп Î Акр, то принимается альтернативная гипотеза
. Если jэмп Î Акр, то принимается альтернативная гипотеза 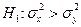 , а если jэмп Ï Акр, то принимается основная гипотеза
, а если jэмп Ï Акр, то принимается основная гипотеза 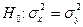 .
.
2. Проверка гипотезы 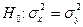 при наличии альтернативной гипотезы
при наличии альтернативной гипотезы 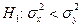 сводится к п. 1, т.е. к проверке основной гипотезы
сводится к п. 1, т.е. к проверке основной гипотезы 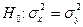 при наличии альтернативной
при наличии альтернативной 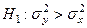 . Отличие будет состоять лишь в том, что теперь хкр – это корень уравнения
. Отличие будет состоять лишь в том, что теперь хкр – это корень уравнения 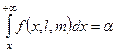 .
.
3. Проверка основной гипотезы 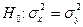 при наличии альтернативной
при наличии альтернативной 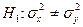 сводится к вычислению статистики
сводится к вычислению статистики 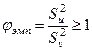 , где
, где  - наибольшая из дисперсий
- наибольшая из дисперсий 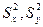 , а
, а 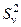 - наименьшая, и вычислению критической области
- наименьшая, и вычислению критической области 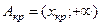 , где хкр ³ 1 и является корнем уравнения
, где хкр ³ 1 и является корнем уравнения 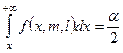 , где m - число степеней свободы набольшей выборочной дисперсии.
, где m - число степеней свободы набольшей выборочной дисперсии.
Как и прежде, если jэмп Î А кр, то принимается альтернативная гипотеза 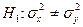 , а если jэмп Ï Акр, то - основная гипотеза
, а если jэмп Ï Акр, то - основная гипотеза 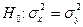 .
.
П р и м е р № 1. Пусть независимые случайные величины 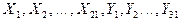 нормально распределены и имеют одинаковые дисперсии. Найти значения х1, х2, х3, х4 такие, что для случайной величины
нормально распределены и имеют одинаковые дисперсии. Найти значения х1, х2, х3, х4 такие, что для случайной величины 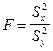 выполняются следующие равенства:
выполняются следующие равенства:
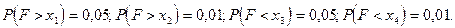
Р е ш е н и е. Как уже говорилось, случайная величина 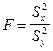 , где
, где 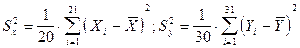 , имеет F - распределение с m = 20 и l = 30 степенями свободы. Вначале найдем х1 > 1 и x2 > 1 такие, что
, имеет F - распределение с m = 20 и l = 30 степенями свободы. Вначале найдем х1 > 1 и x2 > 1 такие, что 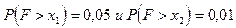 . Имеем
. Имеем
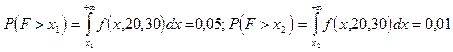 .
.
По табл. 6 Приложения для a = 0,05 и a = 0,01 при m = 20; l = 30 находим: х1 = 1,93; x2 = 2,55.
Теперь заметим, что если 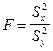 имеет F - распределение с m и l степенями свободы, то случайная величина
имеет F - распределение с m и l степенями свободы, то случайная величина 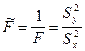 имеет F - распределение с l и m степенями свободы. Поэтому величины х3 < 1 и x4 < 1, удовлетворяющие равенствам
имеет F - распределение с l и m степенями свободы. Поэтому величины х3 < 1 и x4 < 1, удовлетворяющие равенствам 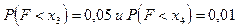 , определяются из уравнений
, определяются из уравнений 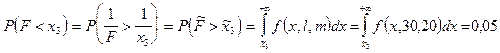 , где
, где 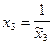 . По табл. 6 находим:
. По табл. 6 находим: 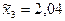 , а следовательно,
, а следовательно, 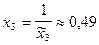 .
.
Аналогично получаем
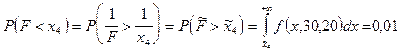 .
.
По табл. 6 находим: 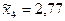 , а
, а 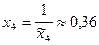 .
.
П р и м е р № 2. Двумя измерительными приборами произведены измерения диаметров валов некоторых изделий, сделанных на одном станке в течение одной смены. Первый измерительный прибор использовали 17 раз, а второй - 25 раз. По результатам измерений вычислили значения исправленных выборочных дисперсий отклонений диаметров валов от номинала. Получено, что
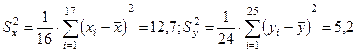 .
.
Проверить на уровне значимости a = 0,01 гипотезу о том, что оба измерительных прибора имеют один класс точности, т.е. дисперсии ошибок измерений приборов одинаковы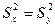 .
.
Р е ш е н и е. Обычно результаты измерений независимы и распределены нормально или приблизительно нормально. Поэтому используем F - критерий. В качестве основной гипотезы Но выбираем 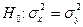 - точности первого и второго прибора одинаковые. За альтернативную гипотезу берем
- точности первого и второго прибора одинаковые. За альтернативную гипотезу берем 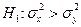 - второй прибор имеет более высокий класс точности. Конкурирующая гипотеза Н1 выбрана такой, потому что
- второй прибор имеет более высокий класс точности. Конкурирующая гипотеза Н1 выбрана такой, потому что 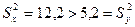 .
.
Статистикой критерия является величина 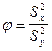 , имеющая F - распределение с (16; 24) степенями свободы. Критическая область имеет вид
, имеющая F - распределение с (16; 24) степенями свободы. Критическая область имеет вид 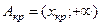 , хкр > 1 есть корень уравнения
, хкр > 1 есть корень уравнения
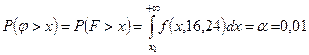 .
.
По табл. 6 Приложения находим хкр = х = 2,85, т.е. 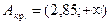 .
.
Значение критерия равно 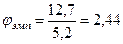 . И так как jэмп Ï
. И так как jэмп Ï 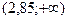 то принимается основная гипотеза
то принимается основная гипотеза 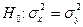 , т.е. измерительные приборы имеют одинаковый класс точности.
, т.е. измерительные приборы имеют одинаковый класс точности.
З а м е ч а н и е. При использовании F - критерия предполагалось, что выборки производились из генеральных совокупностей, имеющих нормальные распределения. Однако опыт и исследования показывают, что F - критерий устойчив по отношению к отклонению от нормального распределения, особенно если объемы выборок не меньше нескольких десятков.
Все критерии, построенные ранее и примененные в примерах этого раздела, называются критериями значимости.
Эти критерии позволяют статистически проверить основную гипотезу 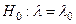 при наличии одной из альтернативных гипотез
при наличии одной из альтернативных гипотез 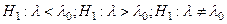 , где l - некоторый параметр генеральной совокупности, из которой производится выборка, а l0 - некоторое заданное число.
, где l - некоторый параметр генеральной совокупности, из которой производится выборка, а l0 - некоторое заданное число.
Например, Т - критерий или F - критерий позволяют проверить, являются ли некоторые различия в наблюдениях двух выборок значимыми (существенными) или случайными.
8.4. Критерий согласия Пирсона
Рассмотрим теперь один из так называемых критериев согласия: критерий Пирсона или хи-квадрат. Критерий согласия Пирсона служит для статистической проверки гипотезы 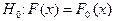 , где
, где 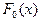 - заданное (гипотетическое) распределение, а
- заданное (гипотетическое) распределение, а 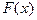 - функция распределения случайной величины Х. Гипотеза Но может иметь вид
- функция распределения случайной величины Х. Гипотеза Но может иметь вид 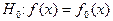 , где
, где 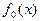 - гипотетическая плотность вероятности, а
- гипотетическая плотность вероятности, а 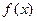 - плотность вероятности распределения случайной величины Х. Для дискретной случайной величины, гипотеза Но имеет вид
- плотность вероятности распределения случайной величины Х. Для дискретной случайной величины, гипотеза Но имеет вид 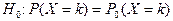 .
.
В начале рассмотрим случай, когда функция распределения 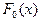 полностью определена, т.е. не содержит неизвестных параметров.
полностью определена, т.е. не содержит неизвестных параметров.
Построение критерия согласия Пирсона начинается с разбиения области возможных значений случайной величины Х на конечное число непересекающихся множеств 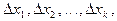 которые называются классами.
которые называются классами.
Если Х - случайная непрерывная величина, то 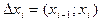 - интервал или полуоткрытый отрезок вида
- интервал или полуоткрытый отрезок вида 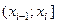 или
или 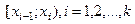 , где k - число классов. Возможны случаи, когда
, где k - число классов. Возможны случаи, когда 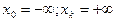 . Это будет, например, когда величина Х нормально распределена. Если согласно гипотезе Но случайная величина равномерно распределена на отрезке
. Это будет, например, когда величина Х нормально распределена. Если согласно гипотезе Но случайная величина равномерно распределена на отрезке 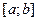 , то
, то 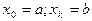 .
.
Для случайной дискретной величины Х её возможные значения 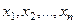 объединяют последовательно в k множеств
объединяют последовательно в k множеств 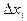 , содержащих соответственно mi значений (
, содержащих соответственно mi значений (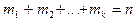 ).
).
Далее, предполагая, что гипотеза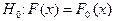 справедлива, вычисляют «теоретические» вероятности попадания случайной величины в класс
справедлива, вычисляют «теоретические» вероятности попадания случайной величины в класс 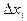 :
: 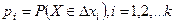 . Для случайной непрерывной величины Х имеем:
. Для случайной непрерывной величины Х имеем: 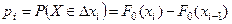 . Если Х - случайная дискретная величина, то pi – это сумма вероятностей для всех mi значений из интервала
. Если Х - случайная дискретная величина, то pi – это сумма вероятностей для всех mi значений из интервала 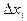 :
: 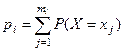 , где хj Î
, где хj Î 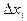 .
.
Разбиение выборки объёма n на классы 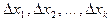 осуществляется произвольно, но при этом следует соблюдать правило: для граничных классов должны выполняться неравенства
осуществляется произвольно, но при этом следует соблюдать правило: для граничных классов должны выполняться неравенства 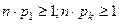 , а для остальных -
, а для остальных - 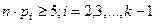 . Для удовлетворения этим условиям возможно объединение некоторых соседних классов в один. Опыт показывает, что число классов желательно брать в пределах от 5 до 15.
. Для удовлетворения этим условиям возможно объединение некоторых соседних классов в один. Опыт показывает, что число классов желательно брать в пределах от 5 до 15.
Итак, пусть все выше перечисленные построения произведены, а необходимые требования выполнены. Пусть 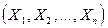 - математическая выборка из генеральной совокупности, порождённой распределением
- математическая выборка из генеральной совокупности, порождённой распределением 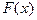 , путь
, путь 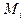 - число случайных величин, попавших в i - ый класс,
- число случайных величин, попавших в i - ый класс, 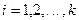 . Тогда в теории вероятностей доказывается, что случайная величина
. Тогда в теории вероятностей доказывается, что случайная величина 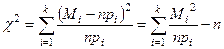 имеет хи-квадрат распределение с m = k – 1 cтепенями свободы.
имеет хи-квадрат распределение с m = k – 1 cтепенями свободы.
Так как c2 есть мера отклонения истинного распределения 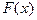 от гипотетического
от гипотетического 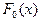 , то в качестве критерия выбирается статистика
, то в качестве критерия выбирается статистика 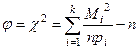 , которая при больших n (около сотни и более) имеет хи-квадрат распределение с m = k - 1 степенями свободы.
, которая при больших n (около сотни и более) имеет хи-квадрат распределение с m = k - 1 степенями свободы.
Критическая область при использовании критерия согласия Пирсона имеет вид 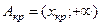 , где хкр > 0 есть корень уравнения
, где хкр > 0 есть корень уравнения 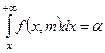 , где
, где 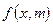 - плотность вероятности случайной величины
- плотность вероятности случайной величины 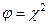 с m степенями свободы, a - уровень значимости критерия j. По табл. 5 Приложения для заданных значений a и m находим хкр. Вычисляем по выборке
с m степенями свободы, a - уровень значимости критерия j. По табл. 5 Приложения для заданных значений a и m находим хкр. Вычисляем по выборке 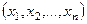 значение критерия
значение критерия 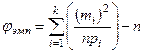 , где m i - число значений из выборки, попавших в i - ый класс
, где m i - число значений из выборки, попавших в i - ый класс 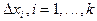 .
.
Если jэмп Î Акр, то гипотеза 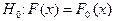 отвергается на уровне значимости a, т.е. принимается решение, вероятность ошибки которого равна a. Если jэмп Ï Акр, то гипотеза Но принимается.
отвергается на уровне значимости a, т.е. принимается решение, вероятность ошибки которого равна a. Если jэмп Ï Акр, то гипотеза Но принимается.
З а м е ч а н и е. Если гипотетическая функция распределения зависит от l неизвестных параметров и для определения 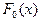 пришлось использовать оценки этих параметров, то схема применения критерия согласия Пирсона остаётся прежней, только изменяется число степеней свободы, его следует брать равным m = k – - l - 1.
пришлось использовать оценки этих параметров, то схема применения критерия согласия Пирсона остаётся прежней, только изменяется число степеней свободы, его следует брать равным m = k – - l - 1.
П р и м е р № 1. В 1890 году был измерен рост 1000 взрослых мужчин - рабочих московских фабрик. Результаты измерений указаны в таблице, в которой верхняя строка – это диапазоны измеренных ростов в см, а нижняя – число мужчин, рост которых попал в соответствующие диапазоны:
| Рост | 143¸146 | 146¸149 | 149¸152 | 152¸155 | 155¸158 |
| Число |
| 158¸161 | 161¸164 | 164¸167 | 167¸170 | 170¸173 | 173¸176 | 176¸179 |
| 179¸182 | 182¸185 | 185¸188 |
Табл. 8.1
Используя критерий согласия Пирсона, на уровне значимости a = 0,01 проверить гипотезу о том, что рост мужчин имеет нормальное распределение.
Р е ш е н и е. Пусть случайная величина - рост мужчины имеет плотность вероятности 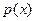 . Требуется на уровне значимости a = 0,01 статистически проверить гипотезу
. Требуется на уровне значимости a = 0,01 статистически проверить гипотезу 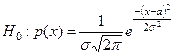 . Эта плотность вероятности зависит от двух параметров: а и s, значит, l = 2.
. Эта плотность вероятности зависит от двух параметров: а и s, значит, l = 2.
В качестве неизвестных параметров 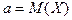 и
и 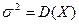 возьмем их оценки, вычисленные по статистической таблице 8.1 (
возьмем их оценки, вычисленные по статистической таблице 8.1 (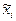 - середина i - ого интервала, mi - число мужчин, рост которых попал в i - ый интервал):
- середина i - ого интервала, mi - число мужчин, рост которых попал в i - ый интервал):
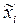
| 144,5 | 147,5 | 150,5 | 153,5 | 156,5 | 159,5 | 162,5 |
| mi |
| 165,5 | 168,5 | 171,5 | 174,5 | 177,5 | 180,5 | 183,5 | 186,5 |
Заметим, что
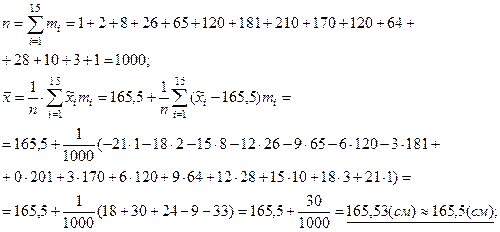
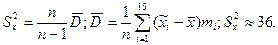
З а м е ч а н и е. Расчет 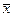 и
и 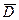 удобно производить на современных инженерных калькуляторах, имеющих соответствующие функциональные клавиши.
удобно производить на современных инженерных калькуляторах, имеющих соответствующие функциональные клавиши.
В качестве 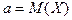 и
и 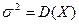 берём
берём 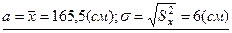 .
.
Множество возможных значений случайной величины Х разобьем на 11 классов (крайние три интервала, стоящие и слева, и справа в табл. 8.1, объединяем):
| Рост | -¥¸152 | 152¸155 | 155¸158 | 158¸161 | 161¸164 |
| Число |
| 164¸167 | 167¸170 | 170¸173 | 173¸176 | 176¸179 | 179¸+¥ |
Вычислим теоретические вероятности
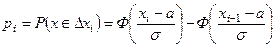 ,
,
где Ф (х) - функция Лапласа, значения которой приводятся в табл. 2 Приложения.
Итак,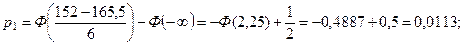
при этом 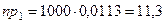 ;
;
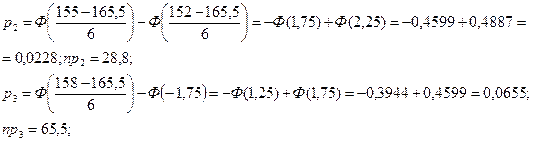
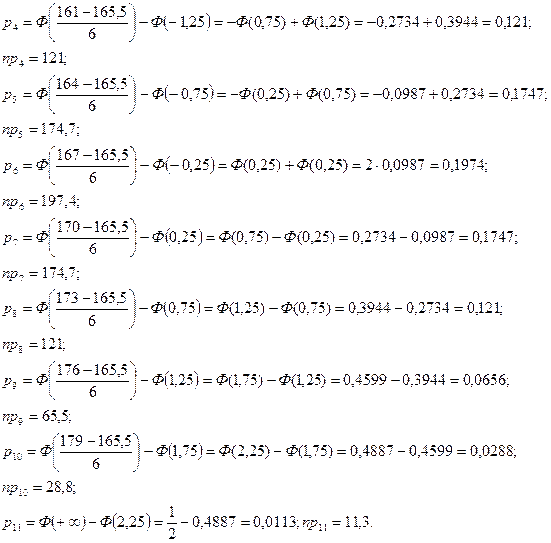
Составим таблицу эмпирических чисел mi и теоретических чисел nрi мужчин, попавших в i - ый класс, i = 1,2,3,...11.
| mi | |||||||||||
| nрi | 11,3 | 28,8 | 65,5 | 174,7 | 197,4 | 174,7 | 65,5 | 28,8 | 11,3 |
Вычисляем значение критерия
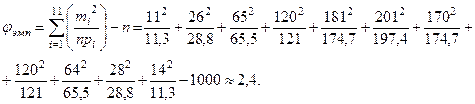
Число степеней свободы равно m = k - l - 1 = 11 – 2 - 1 = 8. Для уровня значимости a = 0,01 и m = 8 по табл. 4 Приложения находим корень уравнения 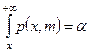 : хкр = х = 20,1. Следовательно, критической областью Акр будет открытый интервал (20,1; + ¥). Поскольку jэмп Ï Акр, то на уровне значимости a = = 0,01 принимается гипотеза о нормальном распределении роста мужчин с плотностью вероятности
: хкр = х = 20,1. Следовательно, критической областью Акр будет открытый интервал (20,1; + ¥). Поскольку jэмп Ï Акр, то на уровне значимости a = = 0,01 принимается гипотеза о нормальном распределении роста мужчин с плотностью вероятности 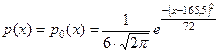 .
.
П р и м е р № 2. За время второй мировой войны на Лондон упало 537 самолётов-снарядов. Вся территория Лондона была разделена на 576 участков площадью по 0,25 кв. км. В приводимой ниже таблице указаны числа участков mi, на которые упало хi самолётов-снарядов:
| хi | 5 и больше | |||||
| m i |
Как и положено, объём выборки 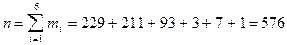 .
.
С помощью критерия согласия Пирсона проверить, согласуются ли эти данные с гипотезой о том, что число самолётов-снарядов, попавших на один участок, распределено по закону Пуассона с параметром l, значения которого равно значению выборочного среднего. Уровень значимости принять равным a = 0,05.
Р е ш е н и е. В среднем на один участок попало 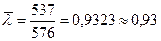 самолёта-снаряда. Поэтому единственный (l = 1) параметр l распределения Пуассона полагаем равным l =
самолёта-снаряда. Поэтому единственный (l = 1) параметр l распределения Пуассона полагаем равным l =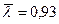 .
.
Рассмотрим случайную величину Х - число попаданий снарядов на один участок. Нулевая гипотеза, которую надо статистически проверить, записывается как 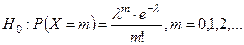 .
.
Разобьем весь диапазон возможных значений величины Х на шесть классов:
Dх1 - на участок не упал ни один самолёт-снаряд;
Dх2 - на участок упал один самолёт-снаряд;
Dх3 - на участок упало два самолёта-снаряда;
Dх4 - на участок упало три самолёта-снаряда;
Dх5 - на участок упало четыре самолёта-снаряда;
Dх6 - на участок упало пять и более самолётов-снарядов.
Вычислим теоретические вероятности:
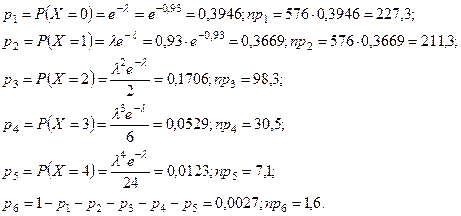
Эмпирические и теоретические числа самолетов - снарядов попавших в i -ый класс, i = 1,2,...,6 собраны в таблицу
| mi | ||||||
| nрi | 227,3 | 211,3 | 98,3 | 30,5 | 7,1 | 1,6 |
Вычисляем значение критерия
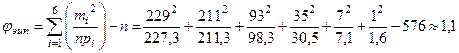 .
.
Число степеней свободы равно m = k - l - 1 = 6 - 1 - 1 = 4. Критическая область Акр имеет вид: 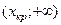 , где хкр есть корень уравнения
, где хкр есть корень уравнения 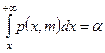 . По табл. 5 Приложения для a = 0,05 и m = 4 находим хкр = 9,5. Итак,
. По табл. 5 Приложения для a = 0,05 и m = 4 находим хкр = 9,5. Итак, 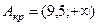 .
.
Поскольку jэмп Ï Акр, то на уровне значимости a = 0,05 принимается гипотеза Но, т.е. число самолётов-снарядов, упавших на один участок площадью 0,25 кв. км в Лондоне, подчиняется закону Пуассона с параметром l = 0,93.
 2014-01-24
2014-01-24 865
865








