Из тригонометрии известно, что
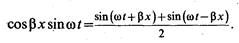
Следовательно, напряжение и ток в линии можно представить суммой двух составляющих, каждая из которых является уравнением бегущей волны:
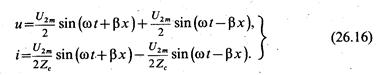
Первое слагаемое в этих уравнениях — прямая волна, распространяющаяся от начала к концу линии; второе — обратная волна с такой же амплитудой.
В этом можно убедиться, рассмотрев подробно одну из составляющих, например первую в уравнении напряжения.
Предположим, что некоторая величина напряжения u’ в момент времени t имеет место в пункте, пространственное положение которого определяется расстоянием х от конца (или начала) линии (см. рис. 26.5)
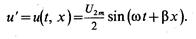
Распространение волны напряжения означает, что через бесконечно малый промежуток времени dt такое же напряжение u’ возникает в другом пункте линии, отстоящем от первого на бесконечно малое расстояние dх:
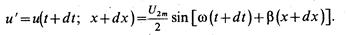
Равенство напряжений в моменты времени, отстоящие на dt, возможно при равенстве аргументов синусов в обоих уравнениях, т. е. при
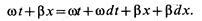
Отсюда
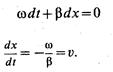
Отношение dx/dt характеризует скорость распространения волны напряжения вдоль линии и называется фазовой скоростью волны.
Знак минус указывает на то, что волна движется от начала к концу линии (расстояние х уменьшается).
Аналогично можно показать, что вторая составляющая напряжения в уравнении (26.16) представляет собой волну, распространяющуюся в обратном направлении (х увеличивается).
Волна, распространяющаяся от начала к концу линии, называется прямой или падающей, а волна, распространяющаяся в обратном направлении (от конца линии к началу), — обратной или отраженной.
Те же рассуждения можно отнести к составляющим тока во втором уравнении (26.16).
Таким образом, стоячая волна напряжения представляет собой сумму, а волна тока —-разность прямой (падающей) и обратной (отраженной) волн одинаковой амплитуды.
 2014-01-25
2014-01-25 865
865








