PP1 - главная линия картины, PP1 ^ tt и PP1 ^ hh

SР – перпендикуляр, опущенный из точки зрения S на картинную плоскость К, называется главным лучом (S Р ^ К).

Р = SР ∩ К – главная точка картины;

Ортогональные проекции точек на предметную плоскость П₁, называется основаниями этихточек:

А₁ – основание точки А, расположенной в предметном пространстве;

Р₁ – основание главной точки картины,

S₁ – основание точки зрения или точка стояния.

SS₁ – расстояние от точки зрения до предметной плоскости, называется высотой точки зрения (высотой горизонта) | SS₁ | = | PP₁ |.

PS – расстояние от точки зрения до картины, называется главным расстоянием или дистанционным расстоянием.

А^¢ = АS ∩ К – перспектива точки А.

А₁^¢ = А₁S ∩ К – перспектива основания или вторичная проекция

точки А.

Одним из требований, предъявляемых к чертежу, является его обратимость. Для получения обратимого чертежа при проецировании на одну плоскость проекций необходима вторичная проекция. Таким образом, перспектива точки и её вторичная проекция однозначно определяют положение точки в пространстве. А^¢А₁^¢ – линия связи между перспективой точки и её вторичной проекцией. А^¢А₁^¢ ^ hh; А₁^¢А^¢ // РР₁.

Построение перспективного изображения (рис.16.3) начинают с задания основных элементов перспективного аппарата, принадлежащих картине. Вначале задают горизонтально расположенные линии земли tt, и горизонта hh расстояние между которыми равно высоте точки зрения SS₁. В произвольном месте (обычно по центру) задают главную линию картины, проводя РР₁ перпендикулярно линии горизонта.

Иногда на перспективном изображении показывают дистанционную окружность. Это окружность с центром в точке Р радиусом РD = PS. Точка D называется дистанционной.

По положению вторичной проекции точки (перспективы основания точки) относительно линий hh и tt можно судить о положении точки в пространстве, что видно из схемы перспективного аппарата, изображённой на рис. 16.2, 16.3, 16.4.

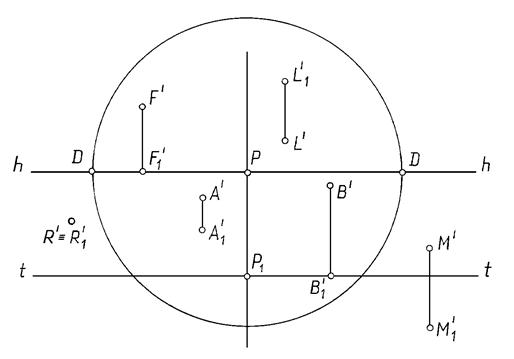
Рис.16.3

Если А₁^¢ находится между линиями hh и tt, то точка А находится в предметном пространстве.

Если М₁^¢ расположена ниже tt, то точка М находится в промежуточном пространстве.

Если L₁^¢ расположена выше линии hh, то точка L находится в мнимом пространстве.

Если В₁^¢ расположена на линии tt, то точка В принадлежит картине.

Если R^¢º R₁^¢, то точка R лежит на плоскости П₁.

Если F₁^¢ расположена на линии hh, то точка F находится в бесконечности, однако показать на чертеже это невозможно.

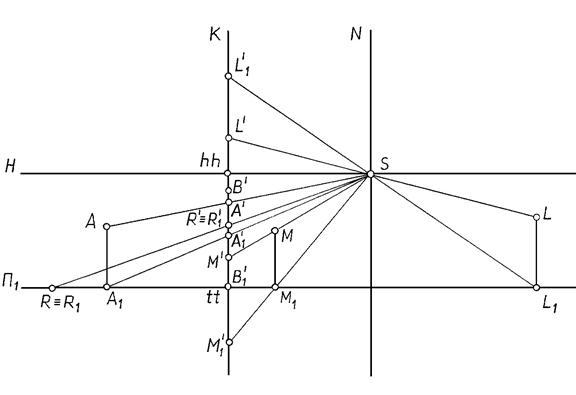
Рис. 16.4