Построение перспективы прямой принадлежащей предметной плоскости

Точка схода –это перспектива несобственной (бесконечно удаленной) точки прямой. Чтобы построить точку схода прямой, необходимо через точку зрения провести луч, параллельный прямой и найти точку пересечения этого луча с картиной. Обозначают точку схода буквой F.

Перспектива прямой

Две точки определяют прямую в пространстве. Чтобы построить перспективу прямой, обычно строят перспективу двух ее точек – картинный след и точку схода прямой (рис. 16.5).

Картинный след – это точка пересечения прямой с картиной.

На рис. 16.5:

1^¢ - картинный след прямой n;

2^¢ - картинный след прямой m.

Если прямые параллельны в пространстве и не параллельны картине, то в перспективе они пересекаются в общей точке схода F (см. рис. 16.5).

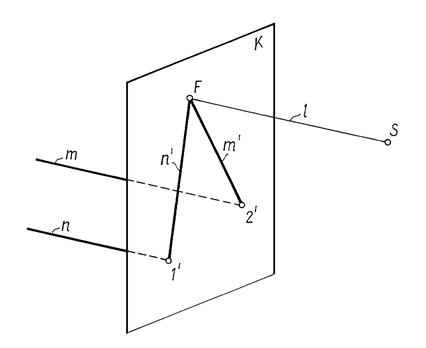
Рис. 16.5

Чтобы построить перспективу прямой по ее ортогональным проекциям, надо найти точку схода и картинный след на ортогональном чертеже, а затем перенести их на перспективное изображение. При необходимости задается дистанционная точка D.

Пример. Построить перспективу прямой l, принадлежащей предметной плоскости (рис. 16. 6)

Решение:

1. На перспективном изображении задаем горизонтальные прямые tt и hh, расстояние между которыми равно высоте точки зрения Z_s. В произвольном месте (обычно по центру) задаем главную линию РР₁.

2. Определяем на ортогональном чертеже картинный след (точку 1) и строим ее в перспективе на tt, отложив Р₁1^¢=Р₁1₁.

3. Определяем точку схода F на ортогональном чертеже:

S₁F₁ // l₁; F₁ = F₁ S ₁ Ç К₁ .

4. Строим перспективу точки схода прямой, отложив на hh PF^¢=P₁F₁.

5. Строим перспективу прямой l^¢, соединяя точки 1^¢ и F^¢ . В данном случае вторичная проекция прямой и ее перспектива совпадают l₁^¢º l^¢.

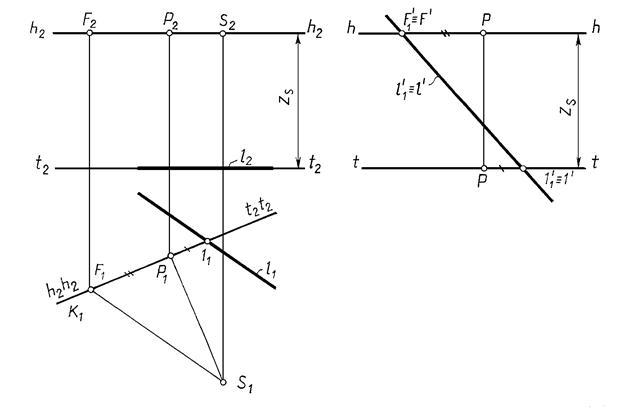
Рис. 16. 6

Пример. Построить перспективу прямой n, принадлежащей предметной плоскости и проходящей через точку стояния S₁ (рис. 16. 7)

Если прямая принадлежит предметной плоскости и проходит через точку стояния S₁, то перспектива ее параллельна главной линии картины РР₁ Рис. 16. 7.

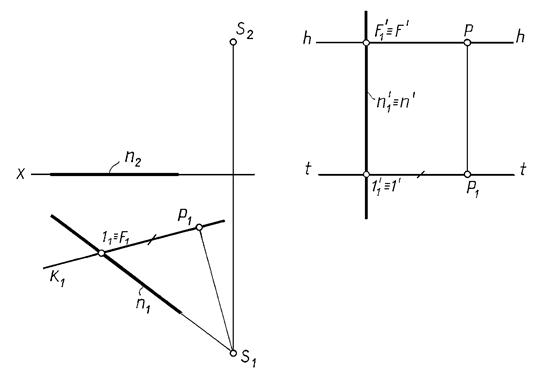
Рис. 16. 7

Пример. Построить перспективу прямой m, принадлежащей предметной плоскости и перпендикулярна картине (рис. 16. 8)

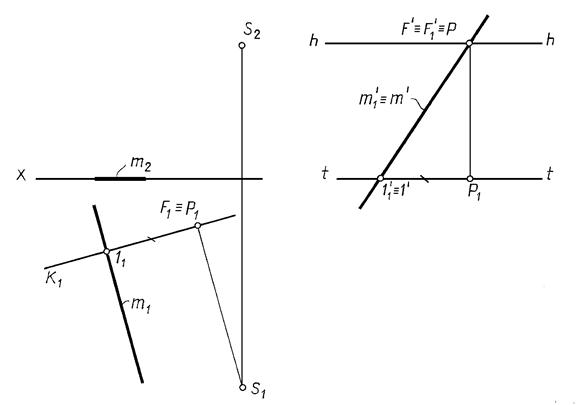
Рис. 16. 8

Если прямая перпендикулярна картине m ^ К, то точка схода ее совпадает с главной точкой картины Р (рис. 16. 8).

Пример. Построить перспективу прямой b, принадлежащей предметной плоскости и составляет с картиной угол 45° (рис. 16. 9)

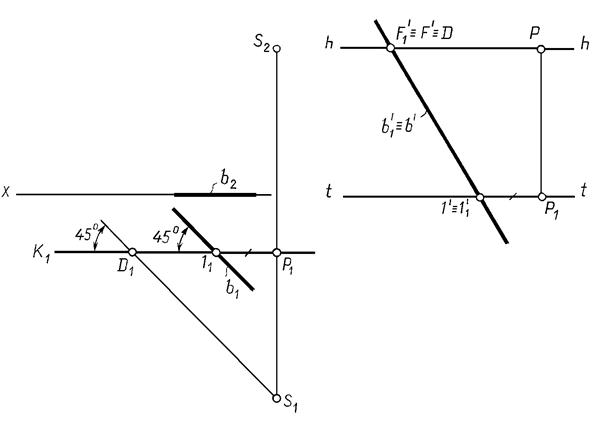
Рис. 16. 9

Если прямая принадлежит предметной плоскости или параллельна предметной плоскости и составляет с картиной угол 45°, то точка схода ее совпадает с дистанционной точкой D. На рис. 16.9 треугольник D₁ P₁ S₁ – равнобедренный, | S₁Р₁ |=| D₁P₁ |, поэтому Fº D.

Перспективу вертикального отрезка нельзя построить по картинному следу и точке схода. Для построения вертикальных отрезков можно воспользоваться способом выноса в картину или боковой стенкой, они будут описаны ниже.