Пример
По данным о стоимости основных производственных фондов (СОПФ) и объеме валовой продукции (ВП) определить линейное уравнение связи.
| Номер предприятия | СОПФ (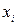 ), млн. руб. ), млн. руб.
| ВП (y), млн. руб. | 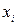 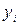
| 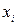 2 2
| 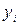 2 2
| 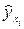
| 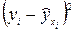
| 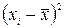
|
| 19,4 | 0,36 | 20,25 | ||||||
| 12,25 | ||||||||
| 30,6 | 0,16 | 6,25 | ||||||
| 36,2 | 27,04 | 2,25 | ||||||
| 41,8 | 3,24 | 0,25 | ||||||
| 47,4 | 73,96 | 0,25 | ||||||
| 2,25 | ||||||||
| 58,6 | 1,96 | 6,25 | ||||||
| 64,2 | 17,64 | 12,25 | ||||||
| 69,8 | 0,04 | 20,25 | ||||||
| Сумма | 125,4 | 82,5 | ||||||
| Среднее | 5,5 | 44,5 | 290,7 | 38,5 | 2248,7 | 44,5 |
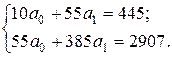
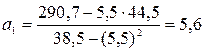 ;
;
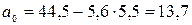 .
.
Уравнение регрессии имеет вид:
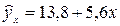 .
.
Следовательно, с увеличением стоимости основных фондов на 1 млн.руб. объем валовой продукции увеличивается в среднем на 5,6 млн. руб.
Проверим значимость полученных коэффициентов регрессии. Рассчитаем 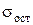 и
и 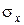 :
:
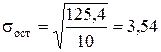
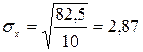
для параметра а 0: 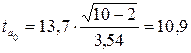
для параметра а 1: 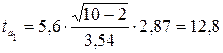 .
.
По таблице Стьюдента с учетом уровня значимости 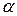 =5% и числа степеней свободы ν =10-1-1=8 получаем
=5% и числа степеней свободы ν =10-1-1=8 получаем 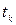 =2,306.
=2,306.
Фактические значения 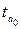 и
и 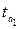 превышают табличное критическое значение
превышают табличное критическое значение 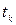 . Это позволяет признать вычисленные коэффициенты корреляции типичными.
. Это позволяет признать вычисленные коэффициенты корреляции типичными.
Пример По данным предыдущего примера оценить тесноту связи между признаками, оценить значимость найденного коэффициента корреляции.
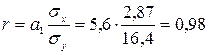 , или
, или 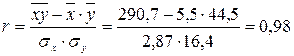 .
.
Значение коэффициента корреляции свидетельствует о сильной прямой связи между рассматриваемыми признаками.
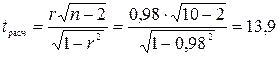
Значение t расч превышает найденное по таблице значение 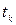 =2.306, что позволяет сделать вывод о значимости рассчитанного коэффициента корреляции.
=2.306, что позволяет сделать вывод о значимости рассчитанного коэффициента корреляции.
Пример Имеются некоторые данные о среднегодовой стоимости ОПФ (СОПФ), уровне затрат на реализацию продукции (ЗРП) и стоимости реализованной продукции (РП). Считая зависимость между этими показателями линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели.
| СОПФ (х 1), млн.руб. | ЗРП (х 2), в % к РП | РП (y), млн.руб. | 
| 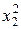
| х 1 х 2 | х 1 y | х 2 y | 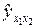
|
| 20,36 | ||||||||
| 20,05 | ||||||||
| 24,21 | ||||||||
| 26,91 | ||||||||
| 30,54 | ||||||||
| 29,08 | ||||||||
| 33,24 | ||||||||
| 35,01 | ||||||||
| 36,25 | ||||||||
| 38,33 | ||||||||
| S = 66 | S = 90 | S = 294 | S = 490 | S = 1018 | S = 688 | S = 2078 | S = 2880 | S = 294 |
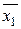 =6,6 =6,6
| 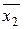 =9,0 =9,0
| 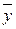 =29,4 =29,4
| – | – | 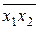 =68,8 =68,8
| 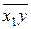 =207,8 =207,8
| 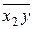 =288,0 =288,0
| – |
Решение. Составим систему нормальных уравнений МНК:
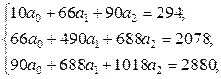
Выразим из 1-го уравнения системы a 0 = 29,4 – 6,6· a 1 – 9· a 2.
Подставив во 2-е уравнение это выражение, получим:
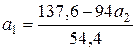 .
.
Далее подставляем в 3-е уравнение вместо a 0 и a 1 полученные выражения и решаем его относительно a 2 с точностью не менее 3-х знаков после запятой. Итак:
a 0 = 12,508; a 1 = 2,672; a 2 = – 0,082; 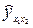 = 12,508 + 2,672· х 1 – 0,082· х 2.
= 12,508 + 2,672· х 1 – 0,082· х 2.
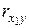 =
= 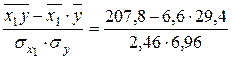 = 0,884;
= 0,884;
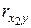 =
= 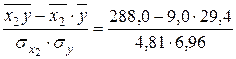 = 0,777;
= 0,777;
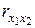 =
= 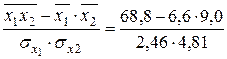 = 0,893;
= 0,893;
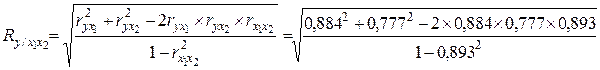 =0,893.
=0,893.
Проверим значимость r (α = 0,01 и ν = 7):
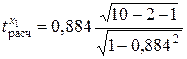 = 5,00;
= 5,00; 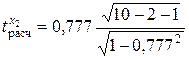 = 3,27.
= 3,27.
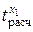 =5,00 > t табл=3,50 – коэффициент корреляции x 1 значим;
=5,00 > t табл=3,50 – коэффициент корреляции x 1 значим;
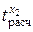 =3,27 < t табл=3,50 – коэффициент корреляции x 2 не значим.
=3,27 < t табл=3,50 – коэффициент корреляции x 2 не значим.
Произведенные расчеты подтверждают условие включения факторных признаков в регрессионную модель – между результативным и факторными признаками существует тесная связь (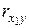 = 0,884;
= 0,884; 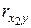 = 0,777), однако между факторными признаками достаточно существенная связь (
= 0,777), однако между факторными признаками достаточно существенная связь (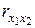 = 0,893). Включение в модель фактора x 2 незначительно увеличивает коэффициент корреляции (
= 0,893). Включение в модель фактора x 2 незначительно увеличивает коэффициент корреляции (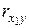 = 0,884;
= 0,884; 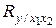 =0,893), поэтому включение в модель фактора x 2 нецелесообразно.
=0,893), поэтому включение в модель фактора x 2 нецелесообразно.
Вычислим стандартизованные коэффициенты уравнения множественной регрессии:
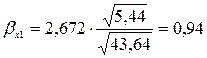
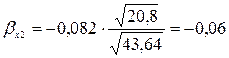
Отсюда вычислим частные коэффициенты детерминации:
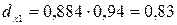
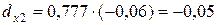
т.е. вариация результативного признака объясняется главным образом вариацией фактора x1.
Вычислим частные коэффициенты эластичности:
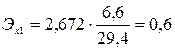
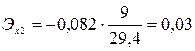
Проверим адекватность модели на основе критерия Фишера:
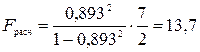
Найдем значение табличного значения F-критерия для уровня значимости α=0,05 и числе степеней свободы ν1 = 2, ν2 = 10 –2 – 1: Fтабл=4,74. Превышение значения Fрасч над значением Fтабл позволяет считать коэффициент множественной детерминации значимым, а соответственно и модель – адекватной, а выбор формы связи - правильным.
 2014-01-25
2014-01-25 728
728








