2014-01-25
700
Пример
Для выравнивания ряда из примера 8.3 используем линейную трендовую модель – уравнение прямой ŷt = a 0 + a 1· t. n = 10. Расчет уравнения регрессии выполним в табличной форме.
Таким образом,
S y =153,4; S y·t = 6,8; S t 2 = 330.
Вычислим параметры a 0, a 1по формулам (8.22, 8.23):
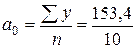= 15,34; 
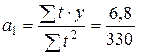= 0,021.
Расчет уравнения регрессии
| Год | y | t | t 2 | y·t | ŷt | yi – ŷt | (yi– ŷt)2 |
| 15,4 | -9 | -138,6 | 15,15 | 0,25 | 0,0625 | ||
| 14,0 | -7 | -98,0 | 15,19 | -1,19 | 1,4161 | ||
| 17,6 | -5 | -88,0 | 15,23 | 2,37 | 5,6169 | ||
| 15,4 | -3 | -46,2 | 15,28 | 0,12 | 0,0144 | ||
| 10,9 | -1 | -10,9 | 15,32 | -4,42 | 19,5364 | ||
| 17,5 | 17,5 | 15,36 | 2,14 | 4,5796 | |||
| 15,0 | 45,0 | 15,40 | -0,40 | 0,0160 | |||
| 18,5 | 92,5 | 15,45 | 3,05 | 9,3025 | |||
| 14,2 | 99,4 | 15,49 | -1,29 | 1,6641 | |||
| 14,9 | 134,1 | 15,53 | -0,63 | 0,3969 | |||
| Итого | 153,4 | 330 | 6,8 | 153,4 | 42,6050 |
Уравнение прямой будет иметь вид:
ŷt = 15,34+0,021· t.
Подставляя в данное уравнение последовательно значения, находим выравненные уровни ŷt (гр. 6 табл. 7.3).
Проверим расчеты:
S y = S ŷt = 153,4.
Следовательно, значения уровней выравненного ряда найдены верно.
|
|
|
Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 1991 по 2000 г. урожайность зерновых культур в среднем возрастала на 0,021 ц/га в год.
Тенденция роста урожайности зерновых культур в изучаемом периоде отчетливо проявляется в результате построения выравненной прямой.
Уровни ряда динамики формируются под влиянием различных взаимодействующих факторов, одни из которых определяют тенденцию развития, а другие –колеблемость (вариацию)
Колебания уровней ряда носят различный характер. Наряду с трендом выделяют циклические (долгопериодические), сезонные (обнаруживаемые в рядах, где данные приведены за кварталы или месяцы) и случайные колебания.
 |
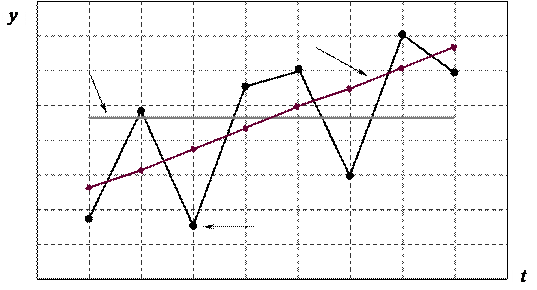– линия тренда
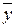– средний уровень
уi – фактические уровни
Колебания фактических уровней yi относительно среднего уровня 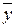и линии тренда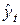
Периодические колебания являются результатом влияния природно-климатических условий, общих экономических факторов, а также многочисленных и разнообразных факторов, которые часто являются регулируемыми.
В широком понимании к сезонным относят все явления, которые обнаруживают в своем развитии четко выраженную закономерность периодических изменений, т.е. более или менее устойчиво повторяющиеся колебания уровней.
Динамический ряд в этом случае называют сезонным рядом динамики.
Метод изучения и измерения сезонности заключается в построении специальных показателей, которые называются индексами сезонности.
Индексами сезонности являются процентные отношения фактических внутригрупповых уровней к теоретическим уровням, выступающим в качестве базы сравнения. Порядок определения индекс сезонности:
|
|
|
1) Для каждого месяца рассчитывается средняя величина уровня
2) Затем вычисляется среднемесячный уровень для всего ряда
3) Определяется показатель сезонной волны – индекс сезонности Is:
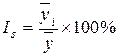, (6.24)
где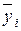 
– средний уровень для каждого месяца;
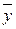– среднемесячный уровень для всего ряда.
Когда уровень проявляет тенденцию к росту или к снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания.
