2014-01-25
711
Ряд Фурье очень компактно записывается в комплексном виде, если воспользоваться формулами Эйлера:
.
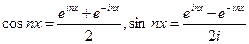Подставив это в формулу (22), сделаем ряд преобразований:
,
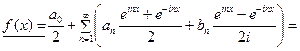
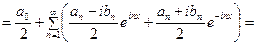
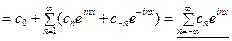где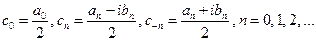 
.
Если вспомнить, как определяются через функцию f (x) коэффициенты Фурье an и bn (формулы (20), (21)), то комплексные коэффициенты Фурье (комплексные амплитуды) окажутся равными
.
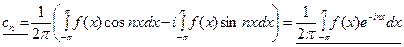Если функция имеет период не 2 p, а 2 l, то по аналогии с формулой (23) получим
,
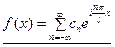где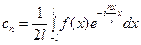 
.
В данном представлении экспоненты с мнимым показателем степени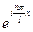 
являются пространственными (если х - координата) или временными (если х - время) гармониками. Множитель 
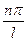называется соответственно волновым числом (k) или циклической частотой (w). Совокупность чисел 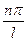- это соответственно пространственный или частотный спектр, который является дискретным.
Если функция непериодическая, то можно считать, что для неё l ® ¥. Для этого случая преобразуем комплексные амплитуды таким образом:
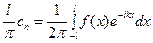, где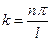 
.
При очень больших l и изменении n на единицу k изменится на очень небольшую величину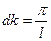 
. Обозначим левую часть равенства через с (k) = 
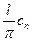. В результате получим 
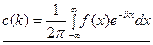. При этом сама функция преобразуется так:
.
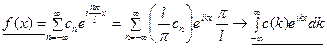Теперь в интеграле волновое число k (или частота w) принимает уже не дискретные значения, а меняется непрерывно. Величина с (k) называется непрерывным спектром волновых чисел (пространственный спектр). Соответственно, если независимая переменная - время, то с (w) называется частотным спектром.
В дифференциальных уравнениях используется преобразование Лапласа:
.
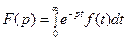В теории рядов есть похожее преобразование Фурье:
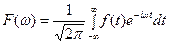
и обратное преобразование Фурье:
.
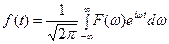Эти формулы можно рассматривать как разложение функции в интеграл Фурье.
К началу К содержанию К титулу
