2014-01-25
719
Рассмотрим последовательность частичных сумм четного количества членов знакочередующегося ряда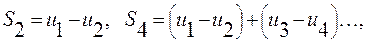 
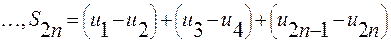
Каждая из разностей, стоящих в скобках, положительна по условию теоремы, значит,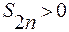 
и последовательность 
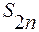является возрастающей.
Если записать эту сумму в виде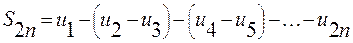 
, то каждая из разностей в скобках положительна и 
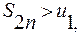то есть последовательность 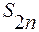ограничена сверху.
Итак, последовательность 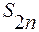является возрастающей и ограничена сверху, следовательно, имеет предел 
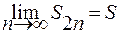, причем 
.
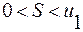Аналогично можно показать сходимость последовательности частичных сумм нечетного количества членов знакочередующегося ряда, следовательно, ряд сходится.
Пример. Знакочередующийся ряд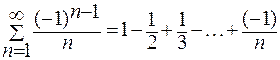 
сходится условно по признаку Лейбница, так как 
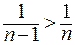и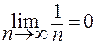 
, но соответствующий ряд из абсолютных величин членов данного ряда является гармоническим 
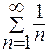и расходится.
Ряд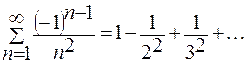 
сходится абсолютно, так как этот знакочередующийся ряд сходится по признаку Лейбница, и ряд 
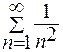сходится тоже.
Замечание. Признак Лейбница используется для приближенного вычисления суммы знакочередующегося ряда с определенной точностью. Сумма отброшенных членов знакочередующегося ряда Лейбница не превосходит первого из них.
Пример. Сколько членов ряда нужно взять, чтобы сумму ряда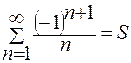 
найти с точностью 0,001?
Представим сумму ряда в ви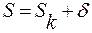де:
, где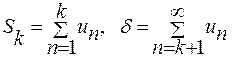 
по признаку Лейбница.
По условию задачи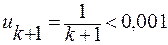 
, откуда 
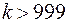нужно взять 
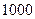членов ряда.
