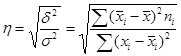 характеризует тесноту связи между результативным и факторным признаками.
характеризует тесноту связи между результативным и факторным признаками.
Для получения представления о форме распределения строят графики распределения (полигон и гистограмму). Число наблюдений, по которому строится эмпирическое распределение, обычно невелико и представляет собой выборку из исследуемой генеральной совокупности. С увеличением числа наблюдений и одновременно уменьшением величины интервала зигзаги полигона начинают сглаживаться, и в пределе мы приходим к плавной кривой, которая называется кривой распределения.
В статистике исследуются различные виды распределения. Как правило, они одновершинные. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин говорит о необходимости перегруппировки данных с целью выделения более однородных групп.
Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. Простейший показатель ассиметрии основан на соотношении показателей центра распределения: чем больше разность между средней арифметической и модой (медианой), тем больше ассиметрия ряда.
Показатель ассиметрии:
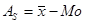 или
или 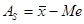 .
.
Для сравнения ассиметрии в нескольких рядах используют относительный показатель ассиметрии.
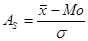 или
или 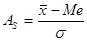
Величина 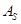 может быть положительной и отрицательной. Если
может быть положительной и отрицательной. Если 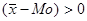 , то на графике такой ряд будет иметь вытянутость вправо (правосторонняя ассиметрия), если
, то на графике такой ряд будет иметь вытянутость вправо (правосторонняя ассиметрия), если 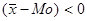 , то вытянутость влево (левосторонняя ассиметрия).
, то вытянутость влево (левосторонняя ассиметрия).
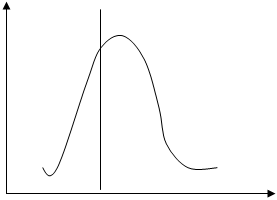 |
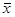
Рис. 7. Правосторонняя ассиметрия
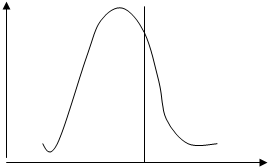 |
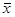
Рис. 8. Левосторонняя ассиметрия
Рассчитывается также показатель характеристики крутости распределения. Это показатель эксцесса. При одной и той же средней арифметической эмпирический ряд может быть островершинным или низковершинным по сравнению с кривой нормального распределения. Показатель эксцесса отражает эту особенность:
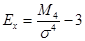 .
.
Если 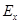 > 0, то эксцесс считают положительным (распределение островершинно), если
> 0, то эксцесс считают положительным (распределение островершинно), если 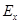 < 0, то эксцесс считается отрицательным (распределение низковершинно).
< 0, то эксцесс считается отрицательным (распределение низковершинно).
 | |||
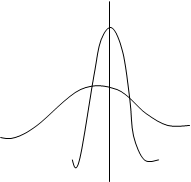 | |||

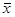
Рис. 9. Положительный эксцесс
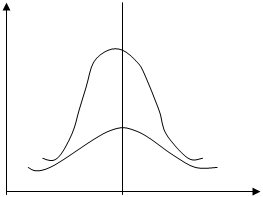 |
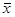
Рис. 10. Отрицательный эксцесс
Среди различных кривых распределения особое место занимает нормальное распределение. Нормальное распределение на графике представляет собой симметричную колоколообразную кривую, имеющую максимум в точке 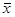 . Эта точка является модой и медианой. Точка перегиба у нормальной кривой находится на расстоянии ±
. Эта точка является модой и медианой. Точка перегиба у нормальной кривой находится на расстоянии ±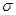 от
от 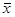 . Кривая нормального распределения выражается уравнением Лапласа
. Кривая нормального распределения выражается уравнением Лапласа
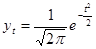 ,
,
где t – нормированное отклонение 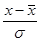 .
.
Установлено, что если площадь, ограниченную кривой нормального распределения, принять за 100%, то можно рассчитать площадь, заключенную между кривой и любыми двумя ординатами. Установлено, что площадь между ординатами, проведенными на расстоянии 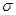 с каждой стороны от
с каждой стороны от 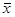 , составляет 0,683 всей площади. Это означает, что 68,3% всех частот (единиц) отклоняются от
, составляет 0,683 всей площади. Это означает, что 68,3% всех частот (единиц) отклоняются от 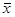 не более, чем на
не более, чем на 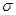 , т.е. находятся в пределах
, т.е. находятся в пределах 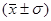 . Площадь, заключенная между ординатами, проведенными на расстоянии 2
. Площадь, заключенная между ординатами, проведенными на расстоянии 2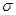 от
от 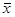 в обе стороны, составляет 0,954, т.е. 95,4% всех единиц совокупности находятся в пределах
в обе стороны, составляет 0,954, т.е. 95,4% всех единиц совокупности находятся в пределах 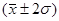 . 99,7% всех единиц находятся в пределах
. 99,7% всех единиц находятся в пределах 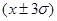 . Это правило трех сигм, характерное для нормального распределения.
. Это правило трех сигм, характерное для нормального распределения.
Нормальное распределение характерно для явлений в биологии и технике. В экономике чаще встречаются умеренно ассиметричные распределения.
Имея дело с эмпирическими распределениями, можно предположить, что каждому эмпирическому распределению соответствует определенная, характерная для него теоретическая кривая. Знание формы теоретической кривой может быть использовано в различных расчетах и прогнозах. Для этого необходимо определить:
общий характер распределения;
по эмпирическим данным построить теоретическую кривую;
определить, насколько эмпирические частоты близки теоретическим.
Введем обозначения:
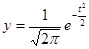 ,
, 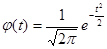 ,
,
где 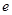 – 2,7182 (основание натурального логарифма)
– 2,7182 (основание натурального логарифма)
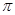 – 3,14.
– 3,14.
Для построения теоретической кривой нормального распределения по эмпирическим данным необходимо найти теоретические частоты
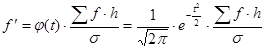 ,
,
где 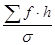 - константа;
- константа;
h – ширина интервала;
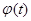 - табулированная величина, которая находится по отклонениям t.
- табулированная величина, которая находится по отклонениям t.
Последовательность расчета теоретических частот следующая:
§ рассчитывается средняя арифметическая ряда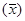
§ рассчитывается среднее квадратическое отклонение 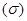
§ находится 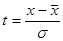
§ по найденным t по таблице находится 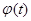
§ рассчитывается 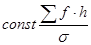
§ каждое значение 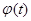 умножается на
умножается на 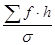 .
.
К числу важнейших теоретических распределений относится распределение Пуассона, которое характерно для редких явлений, причем с увеличением значения x вероятность их наступления падает.
Графически оно имеет следующий вид
.

Рис. 11. Распределение Пуассона
Распределение Пуассона имеет следующий вид:
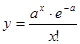 , где
, где 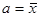
Тогда
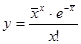
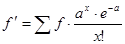 .
.
Нахождение теоретических частот при выравнивании ряда по распределению Пуассона производится в следующем порядке:
· находится средняя арифметическая, 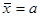
· по таблице определяется 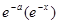
· для каждого значения х определяется теоретическая частота.
Для оценки случайности или существенности расхождений между частотами эмпирического и теоретического распределений в статистике пользуются рядом критериев.
Одним из основных критериев, служащих для сравнения частот эмпирического и теоретического распределений, является критерий согласия Пирсона (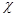 - квадрат)
- квадрат)
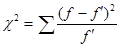
где 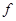 - эмпирические частоты;
- эмпирические частоты;
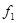 - теоретические частоты.
- теоретические частоты.
Для оценки близости эмпирического распределения к теоретическому определяется вероятность 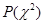 достижения этим критерием данной величины. Если
достижения этим критерием данной величины. Если 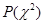 > 0,05, то отклонения фактических частот от теоретических считаются случайными, несущественными. Если
> 0,05, то отклонения фактических частот от теоретических считаются случайными, несущественными. Если 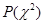 <0,05, то отклонения – существенные, а эмпирическое распределение – принципиально отличное от теоретического. Значения вероятностей
<0,05, то отклонения – существенные, а эмпирическое распределение – принципиально отличное от теоретического. Значения вероятностей 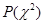 табулирования в зависимости от
табулирования в зависимости от 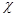 и числа степеней свободы
и числа степеней свободы 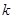 . Для нормального распределения
. Для нормального распределения 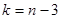 , для распределения по кривой Пуассона:
, для распределения по кривой Пуассона: 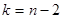 . Зная расчетное
. Зная расчетное 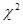 , сравниваем его с табличным (предельным). Если
, сравниваем его с табличным (предельным). Если 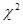 фактическое >
фактическое > 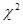 табличного, то расхождение между частотами эмпирического и теоретического распределений нельзя считать случайным. Если
табличного, то расхождение между частотами эмпирического и теоретического распределений нельзя считать случайным. Если 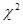 фактическое <
фактическое < 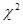 табличного, то расхождение можно считать случайным, а рассматриваемое теоретическое распределение подходящим для описания эмпирического распределения.
табличного, то расхождение можно считать случайным, а рассматриваемое теоретическое распределение подходящим для описания эмпирического распределения.
Критерий Романовского определяется
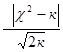 ,
,
где 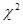 - критерий Пирсона;
- критерий Пирсона;
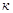 - число единиц степеней свободы.
- число единиц степеней свободы.
Если данный критерий 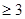 , то расхождения нельзя считать случайными. Если же он < 3, то расхождение между эмпирическими и теоретическими частотами можно считать случайными.
, то расхождения нельзя считать случайными. Если же он < 3, то расхождение между эмпирическими и теоретическими частотами можно считать случайными.
А.Н.Колмогоров предложил критерий, основанный на сопоставлении распределения накопления накопленных частостей (частот).
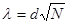 ,
,
где d – максимальная разность между накопленными частостями эмпирического и теоретического рядов распределения, а N – число единиц совокупности. Если же распределение задано в частотах, то
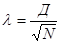 ,
,
где Д – максимальная разность накопленных частот двух распределений.
 2014-01-25
2014-01-25 733
733








