Суперпозиция электромагнитных волн

Одним из основных положений физики является принцип суперпозиции. Это допущение, в соответствии с которым результирующий эффект сложного процесса воздействия представляет собой сумму эффектов, обусловленных каждым воздействием в отдельности, при условии, что эти воздействия не влияют друг на друга. Принцип суперпозиции строго применим к системам, физические состояния которых описываются линейными соотношениями (линейные системы). Например, если среда, в которой распространяется волна S, линейна, то есть её свойства не изменяются под действием возмущений, создаваемых волной, то все эффекты, вызываемые негармонической волной, могут быть определены как сумма эффектов, обусловленных каждой из её гармонических составляющих: .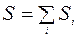

В теории классических полей и в квантовой теории принцип суперпозиции – это положение, в соответствии с которым суперпозиция (то есть результат суммирования, наложения друг на друга) любых допустимых в данных условиях состояний физической системы (или возможных процессов в ней) является также допустимым состоянием (или соответственно возможным процессом). Например, классическое электромагнитное поле в вакууме удовлетворяет принципу суперпозиции: сумма любого числа физически реализуемых полей также физически реализуемое электромагнитное поле.

В классической физике принцип суперпозиции – приближённый принцип, вытекающий из линейности уравнений движения соответствующих систем, например из уравнений Максвелла для электромагнитного поля. Таким образом, он вытекает из более глубоких динамических принципов и поэтому не является фундаментальным. Не является он и универсальным. Например, макроскопическое электромагнитное поле, строго говоря, не подчиняется принципу суперпозиции вследствие зависимости (иногда очень существенной) диэлектрической и магнитной проницаемости среды от внешнего поля.

В разделе «Волновая оптика» ограничимся рассмотрением электромагнитных волн в условиях, когда принцип суперпозиции выполняется.

Пусть в точках А и В (рисунок 2.1) находятся два монохроматических источника, волны от которых доходят до точки наблюдения С.

В соответствии с принципом суперпозиции можно определить закон результирующего колебания, возникающего при этом в точке С.

В общем случае задача состоит в отыскании геометрической суммы векторов, определяющих смещение колеблющейся величины от положения равновесия в произвольный момент времени 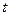, и выяснении характера распределения энергии (интенсивности колебаний) в волновом поле.

Чтобы без ущерба в анализе физической сути явления упростить задачу математически, выделим составляющие векторов смещений, характеризующих колебания в местах расположения источников, перпендикулярные прямой, проходящей через точку наблюдения. Этот выбор обусловлен тем, что электромагнитные волны поперечны. Благодаря этому приёму мы сведем проблему к сложению волн, характеризуемых циклическими частотами колебани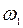й и 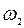, и распространяющихся беспрепятственно к точке наблюдения соответственно от двух монохроматических источников 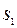и 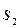, расположенных с ней на одной прямой.

В таком случае в точке С, лежащей на прямой ОХ и удаленной от источников 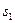и 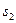соответственно на расстояния 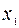и 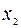, складываются колебания, описываемые уравнениями

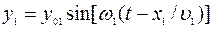, (2.1)

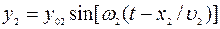, (2.2)

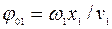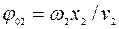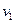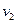в которых величины и определяют сдвиги фаз волн по отношению к колебаниям источников, связанные с конечностью скоростей и распространения волн в среде. В зависимости от природы волн (механические, электромагнитные и т.п.) в качестве 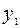и 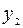могут выступать величины смещений от положения равновесия, напряженности электрических полей и другие величины. Воспользовавшись принципом суперпозиции для волн, легко найти закон, по которому происходит результирующее колебание в точке С:

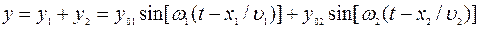. (2.3)

Чтобы избежать громоздких вычислений, предположим, что амплитуды волн (2.1) и (2.2) одинаковы:

.

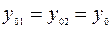Тогда выражение (2.3) примет вид:

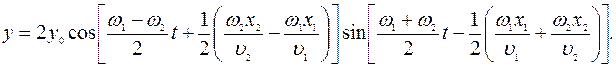
(2.4)

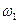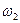При заданных источниках монохроматических волн (и известны и постоянны) и неизменности свойств среды, в которой распространяются волны (это означает, что 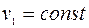и 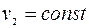), величины 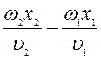и 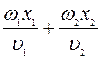зависят лишь от положения точки наблюдения относительно источников и не зависят от времени (рисунок 2.2).

Первые слагаемые в аргументах косинуса и синуса в выражении (2.4) с течением времени будут изменяться по линейному закону:

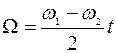, (2.5)

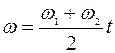. (2.6)

Сравнивая уравнения (2.1), (2.2) и выражение (2.4), последнее можно истолковать как уравнение волны с частотой 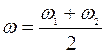и амплитудой

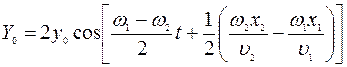, (2.7)

зависящей как от места наблюдения и частоты колебаний источников, так и от времени.

Если 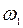мало отличается от 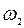, то результирующее колебание в точке С носит характер биений (рисунок 3).

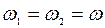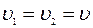Если же предположить, что , то и

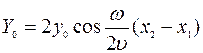, (2.8)

то есть амплитуда результирующего колебания зависит от места наблюдения и не зависит от времени (рис. 4).

	y
			Рис. 4

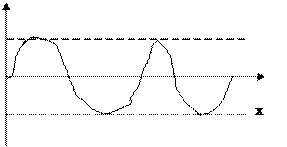Она максимальна в точках, для которых

,

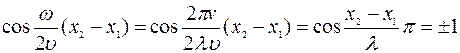что реализуется при

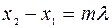, (2.9)

и минимальна в точках, для которых

,

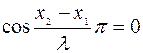что имеет место тогда, когда различие в удалении источников от точки наблюдения составляет нечётное число половин длины волны:

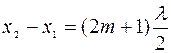. (2.10)

В формулах (2.9), (2.10) 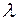– длина волны, 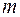– целое число.

Оценим теперь интенсивность результирующих колебаний. С этой целью, считая 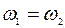, , 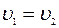, 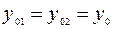представим сначала уравнения (2.1) и (2.2) в виде:

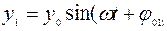, (2.11)

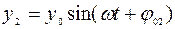, (2.12)

где

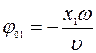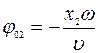, (2.13)

– начальные фазы колебаний, обусловленных в точке наблюдения каждым источником.

Результирующее колебание можно описать уравнением

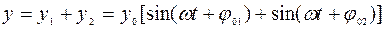. (2.14)

Из теории колебаний известно, что энергия колебаний (интенсивность волн) пропорциональна квадрату смещения от положения равновесия: 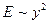. Поэтому получим:

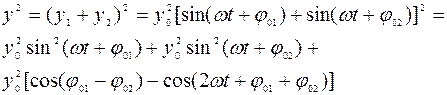. (2.15)

Поскольку все приёмники, используемые для измерения энергии, инерционны, то выражение (2.15) следует усреднить по времени реакции приёмника 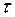, которое, как правило, значительно больше периода колебаний : .

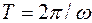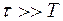Так как , ,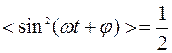

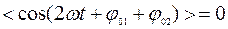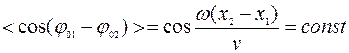, то из выражения (2.15) следует, что

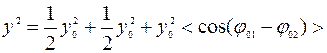. (2.16)

Заметим, что первые два слагаемых в выражениях (2.15) и (2.16) определяют интенсивность колебаний, вызываемых в точке наблюдения каждым из источников 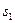и 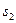в отсутствие другого: 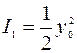; 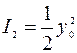. Поэтому величину 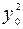можно представить в виде 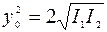, после чего выражение (2.16) преобразуется к форме

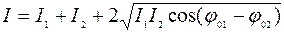. (2.17)

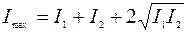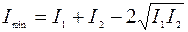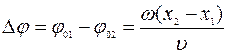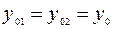Отсюда следует, что интенсивность результирующего колебания не равна сумме интенсивностей складывающихся колебаний, а изменяется от точки к точке в пределах от до в зависимости от величины разности начальных фаз колебаний . При и , .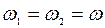

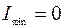Взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве называется интерференцией волн.

Термин «интерференция» происходит от латинского 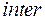(взаимно, между) и 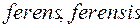(несущий, переносящий) или 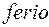(ударяю, поражаю).

Обычно под интерференционным эффектом понимают отличие результирующей интенсивности волнового поля от суммы интенсивностей налагающихся волн.

Мы не случайно до сих пор не конкретизировали природу волн. Интерференция является одним из основных свойств волн любой природы, лишь бы свойства среды допускали их существование (например, упругие волны не существуют в вакууме).

Вернемся к выражениям (2.8) и (2.17). То, что под влиянием двух воздействий объект наблюдения (например, частица среды), находящийся в точке, в которой 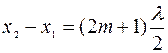, остаётся в покое (колеблется с амплитудой, равной нулю), недоумения не вызывает. Все мы помним и первый закон Ньютона, и историю про воз, который «и ныне там». Так что претензий к выражению (2.8) нет. А что следует из выражения (2.17)? В одном и том же месте сложились два колебания, характеризуемые энергиям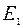и и 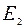, и … энергия исчезла?! Закон сохранения энергии не выполняется?!

Парадокс этот – лишь кажущийся. Изменяясь в указанных выше пределах, энергия перераспределяется в пространстве так, что в одних точках интенсивность колебаний равна 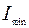, в других она равна 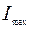, а в остальных удовлетворяет условию 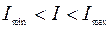(рисунок 5).

Распределение интенсивностей будут стационарным (не зависящим от времени), если интерферирующие волны когерентны, то есть характеризуются одинаковой частотой (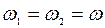) и неизменной во времени разностью начальных фаз колебаний в точке наблюдения.

Если бы мы рассмотрели суперпозицию произвольно ориентированных векторов смещений то выяснилось бы и третье требование: векторы не должны быть ортогональны друг другу, или иначе: волны должны быть поляризованы так, чтобы векторы 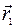и 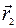имели отличные от нуля проекции на выделенное направление.

Если указанные выше условия выполнены, то говорят, что источники когерентны. Выполнение условий когерентности влечет за собой образование устойчивой интерференционной картины, под которой понимают распределение интенсивностей в области волнового поля, где волны налагаются друг на друга. Если же волны некогерентны, то за время усреднения 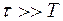разность фаз интерферирующих волн 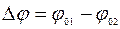многократно изменяется, среднее значение 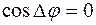и интенсивность колебаний во всех точках, до которых доходят интерферирующие волны, равна сумме интенсивностей отдельных волн: 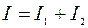. Именно в таком случае выполняется закон независимого действия световых пучков, знакомый учащимся по курсу физики 8-го класса.

Рассмотрим частный случай интерференции, когда налагаются волны, распространяющиеся навстречу друг другу (рисунок 2.5).

Пусть волна распространяется от источника S в направлении препятствия, находящегося на расстоянии l от источника, и отражается в точке A. Навстречу друг другу распространяются две волны:

- падающая

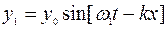(2.17)

- и отражённая

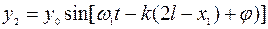. (2.18)

В отсутствие ослабления волны при отражении амплитуды обеих волн одинаковы. При отражении волны от оптически менее плотной среды фазовый сдвиг φ = 0; при отражении от оптически более плотной среды происходит сдвиг фазы на угол φ = π.

Сложим уравнения (2.17) и (2.18) и получим уравнение стоячей волны:

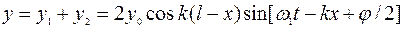. (2.19)

Так как величина 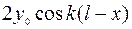не зависит от времени, то её модуль можно рассматривать как амплитуду стоячей волны:

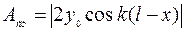. (2.20)

Зная выражение амплитуды, можно найти координаты узлов и пучностей.

Узлы возникнут в точках, в которых амплитуда стоячей волны равна нулю:

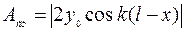= 0.

Из этого условия найдем:

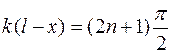, (2.21)

где n = 0, ±1, ±2, ….

Максимумы амплитуды (пучности стоячей волны) формируются в точках, в которых модуль амплитуды волны максимален, то есть при выполнении условия

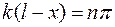, (2.22)

где n = 0, ±1, ±2, ….

Из формул (2.21) и (2.22) найдём соответственно координаты узлов и пучностей стоячей волны:

;

.

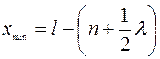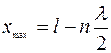Распределению интенсивностей в стоячей волне соответствует рисунок 2.7а (если отражение происходит без потери полуволны) или рисунок 2.7б (если потеря полуволны имеет место).

Таким образом, в стоячей волне соседние узлы находятся на расстоянии λ/2 друг от друга, соседние пучности – на таком же расстоянии: расстояние от узла до ближайшей пучности равно λ/4.

Заметим, что длина стоячей волны (расстояние между соседними пучностями; расстояние между соседними узлами) вдвое меньше длины бегущей волны: .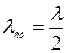

Световые стоячие волны впервые экспериментально обнаружены в 1890 г. О. Винером. Волны определённой длины волны отражались от металлического зеркала АВ (рисунок 2.8) и образовывали систему стоячих волн.

Под острым углом φ к зеркалу располагалась прозрачная стеклянная пластинка, на которую наносился слой фотографической эмульсии, сделанной из коллодия (толщина слоя около λ/20). В местах пучностей (отмечены пунктиром) происходил фотографический процесс. После проявления фотопластинка в этих местах оказывалась почерневшей; в местах узлов слой эмульсии не изменялся. Расстояние между соседними пучностями равно половине длины световой волны. Расстояние между соседними почерневшими полосками на фотоэмульсии равно

.

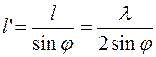При малом угле φ расстояние l´ значительно больше длины волны, и образовавшиеся на пластинке полосы легко заметить. В опытах Винера использовали φ ~ 1°, чему соответствовали расстояния l´~ 1 мм. Вблизи поверхности зеркала образовывался узел, что было доказательством изменения фазы на π при отражении света от зеркала.

Образование стоячих волн может быть использовано для получения цветных фотографий. Предлагаю вам самостоятельно объяснить физическую суть этого процесса после подробного изучения явления интерференции световых волн.

Из формулы (2.7) следует, что с ростом разности частот интерферирующих волн растет скорость изменения амплитуды результирующего колебания:

.

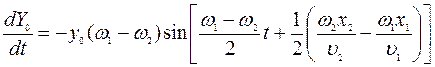Особенно велика эта скорость для электромагнитных волн оптического диапазона (для них υ ~ 10¹⁴ – 10¹⁶ Гц). В этом случае для экспериментального обнаружения быстрых колебаний суммарной интенсивности освещения при работе двух источников необходима техника, способная регистрировать световые импульсы продолжительностью 10^-9 – 10^-10 с. В ее отсутствие для получения для получения интерференционных картин, доступных для наблюдения и анализа, в оптике пользуются искусственным приемом. Сначала создают когерентные источники посредством искусственного разделения световых импульсов по волновому фронту или по амплитуде на две или более частей, затем обеспечивают последующее наложение этих частей после прохождения ими неодинаковых путей. Только в тех случаях, когда в распоряжении исследователя есть два лазера, генерирующих изучение одной и той же частоты, нет необходимости в указанном разделении пучков.

Рассмотрим далее некоторые способы создания когерентных источников и общую схему расчета интерференционных картин, вводя попутно необходимые физические понятия.

Пусть в непрозрачной пластине П, удаленной от экрана Э на расстояние L, имеются две узкие щели s₁ и s₂, симметрично расположенные относительно прямой OS на малом по сравнению с L расстоянием 2l (2l<<L) друг от друга и освещаемые светом, излучаемым источником s и прошедшим сквозь щель s₀ (рис. 6).

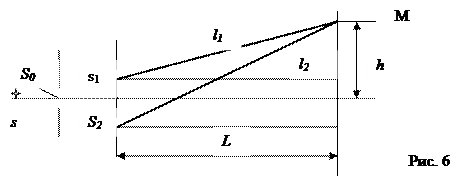В соответствии с принципом Гюйгенса-Френеля, щели s₁ и s₂ выступают в роли источников вторичных волн. Сферические волны, исходящие из каждой точки s₁ и s₂, распространяясь в направлении экрана, интерферируют. На экране наблюдается устойчивая интерференционная картина. Действительно, источники s₁ и s₂ появились как результат деления волнового фронта волн, распространяющихся от щели s₀ до диафрагмы П, и, следовательно, частоты излучаемых ими волн одинаковы. Неподвижность всех элементов схемы Юнга относительно друг друга обеспечивает постоянство разности фаз для волн, приходящих в точку наблюдения М, лежащую в области интерференции.

Определим, какова разность расстояний 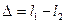, пройденных до точки М волнами, испущенными соответственно источниками s₁ и s₂. Величину

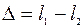(2.18)

называют разностью хода волн (разностью хода лучей). Обозначив через h расстояние от оси симметрии системы до точки наблюдения М и воспользовавшись теоремой Пифагора, найдём:

,

.

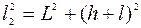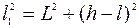Вычитая почленно второе уравнение из первого, получим:

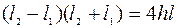. (2.19)

Заметим, что при 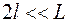расстояния 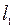и 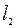мало отличаются от 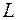. Это даёт основание считать 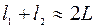. С учётом этого соотношения и определения (2.18) выражение (2.19) можно переписать в виде:

,

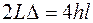откуда

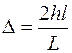. (2.20)

Если разность хода 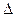в точке М окажется кратной целому числу длин волн (чётному числу полуволн), то есть при

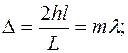
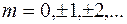, (2.21)

то в точке М имеет место интерференционный максимум. При

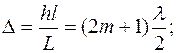
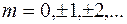(2.22)

в точке наблюдения регистрируется минимальная интенсивность излучения. Целое число 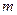называют порядком интерференции.

Разрешив выражения (2.21) и (2.22) относительно 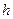, легко найти координаты точек экрана, в которых имеют место максимумы и минимумы освещенности:

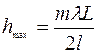, (2.23)

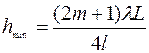. (2.24)