Рис.9
Рис.8
Рис.7
Рис.6
Тогда за промежуток времени 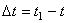 скорость точки получает приращение
скорость точки получает приращение 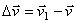 . Для построения вектора
. Для построения вектора 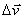 отложим от точки М вектор, равный
отложим от точки М вектор, равный 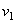 , и построим параллелограмм, в котором диагональю будет
, и построим параллелограмм, в котором диагональю будет 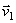 , a одной из сторон
, a одной из сторон 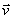 . Тогда, очевидно, вторая сторона и будет изображать вектор
. Тогда, очевидно, вторая сторона и будет изображать вектор 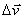 . Заметим, что вектор
. Заметим, что вектор 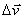 всегда направлен в сторону вогнутости траектории.
всегда направлен в сторону вогнутости траектории.
Отношение приращения вектора скорости 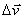 к соответствующему промежутку времени
к соответствующему промежутку времени 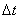 определяет вектор среднего ускорения точки за этот промежуток времени:
определяет вектор среднего ускорения точки за этот промежуток времени:
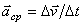 .
.
Вектор среднего ускорения имеет то же направление, что и вектор 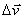 , т. е. направлен в сторону вогнутости траектории.
, т. е. направлен в сторону вогнутости траектории.
Ускорением точки в данный момент времени t называется векторная величина 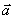 , к которой стремится среднее ускорение
, к которой стремится среднее ускорение 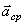 при стремлении промежутка времени
при стремлении промежутка времени 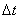 к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
Найдем, как располагается вектор 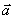 по отношению к траектории точки. При прямолинейном движении вектор
по отношению к траектории точки. При прямолинейном движении вектор 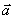 направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения
направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения 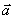 , так же как и вектор
, так же как и вектор 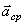 , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор
, лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор 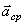 направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке M 1 (рис. 4). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения
направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке M 1 (рис. 4). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения 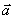 лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
Определение ускорения при координатном способе задания движения
Вектор ускорения точки 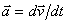 в проекции на оси получаем:
в проекции на оси получаем:
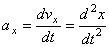 ,
, 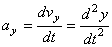 ,
, 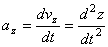
или
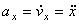 ,
, 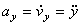 ,
, 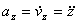 ,
,
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
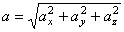 ;
;
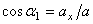 ,
, 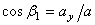 ,
, 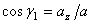 ,
,
где 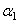 ,
, 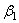 ,
, 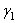 - углы, образуемые вектором ускорения с координатными осями.
- углы, образуемые вектором ускорения с координатными осями.
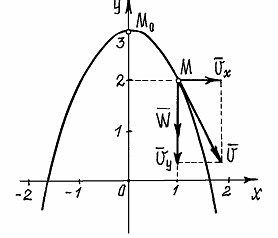
Пример 3. Движение точки задано уравнениями 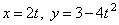 .
.
Из первого уравнения 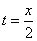 . Подставив во второе, получим уравнение траектории:
. Подставив во второе, получим уравнение траектории: 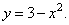
Это уравнение параболы. В начале движения, при 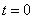 , точка находилась на самом верху, в положении M 0 (
, точка находилась на самом верху, в положении M 0 (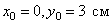 ).
).
А, например, при t =0,5 c она будет в положении M с координатами 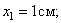
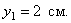
Проекции скорости на оси 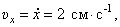
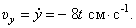
При 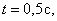
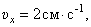
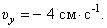
И модуль скорости 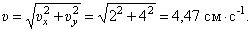
Составляющие скорости по осям и вектор её показаны в масштабе на рис. 7.
Проекции ускорения 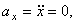
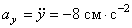 . Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки
При естественном способе задания движения вектор 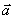 определяют по его проекциям на оси
определяют по его проекциям на оси 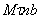 , имеющие начало в точке М и движущиеся вместе с нею (рис.8). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось
, имеющие начало в точке М и движущиеся вместе с нею (рис.8). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось 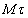 - вдоль касательной к траектории в сторону положительного отсчета расстояния s; ось
- вдоль касательной к траектории в сторону положительного отсчета расстояния s; ось 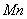 - по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось
- по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось 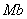 - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль
- перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль  , лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль
, лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль  - бинормалью.
- бинормалью.
Было показано, что ускорение точки  лежит в соприкасающейся плоскости, т.е. в плоскости
лежит в соприкасающейся плоскости, т.е. в плоскости 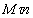 ; следовательно, проекция вектора
; следовательно, проекция вектора 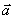 на бинормаль равна нулю (
на бинормаль равна нулю ( ).
).
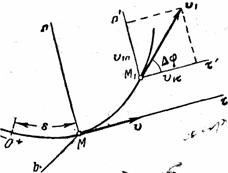
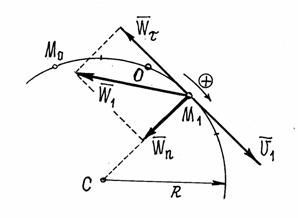
Вычислим проекции 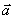 , на две другие оси. Пусть в моментвремени t точка находится в положении М и имеет скорость
, на две другие оси. Пусть в моментвремени t точка находится в положении М и имеет скорость 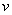 , a в момент
, a в момент 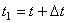 приходит в положение М 1 и имеет скорость
приходит в положение М 1 и имеет скорость 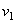 .
.
Тогда по определению
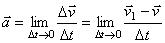 .
.
Перейдем в этом равенстве от векторов к их проекциям на оси 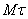 и
и 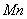 , проведенные в точке М (рис.8). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:
, проведенные в точке М (рис.8). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:
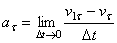 ,
, 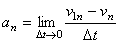 .
.
Учитывая, что проекция вектора на параллельные оси одинаковы, проведем через точку М 1 оси 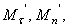 параллельные
параллельные 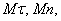 и обозначим угол между направлением вектора
и обозначим угол между направлением вектора 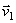 и касательной
и касательной 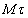 через
через 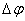 . Этот угол между касательными к кривой в точках М и М 1 называется углом смежности.
. Этот угол между касательными к кривой в точках М и М 1 называется углом смежности.
Напомним, что предел отношения угла смежности 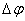 к длине дуги
к длине дуги 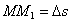 определяет кривизну k кривой в точке М. Кривизна же является величиной, обратной радиусу кривизны
определяет кривизну k кривой в точке М. Кривизна же является величиной, обратной радиусу кривизны 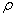 в точке М. Таким образом,
в точке М. Таким образом,
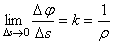 .
.
Обращаясь теперь к чертежу (рис.9), находим, что проекции векторов  и
и  на оси
на оси  будут равны:
будут равны:
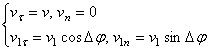 ,
,
где 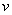 и
и 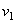 - численные величины скорости точки в моменты
- численные величины скорости точки в моменты 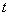 и
и 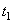 .
.
Следовательно,
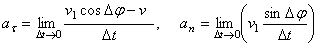 .
.
Заметим что при 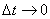 точка М 1 неограниченно приближается к М и одновременно
точка М 1 неограниченно приближается к М и одновременно
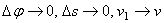 .
.
Тогда, учитывая, что в пределе 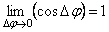 , получим для
, получим для  выражение
выражение
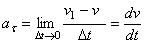 .
.
Правую часть выражения 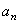 преобразуем так, чтобы в нее вошли отношения, пределы которых нам известны. Для этого умножим числитель и знаменатель дроби, стоящей под знаком предела, на
преобразуем так, чтобы в нее вошли отношения, пределы которых нам известны. Для этого умножим числитель и знаменатель дроби, стоящей под знаком предела, на 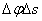 . Тогда будем иметь
. Тогда будем иметь
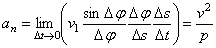 ,
,
так как пределы каждого из стоящих в скобке сомножителей при  равны:
равны:
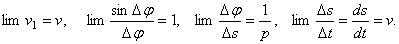
Окончательно получаем:
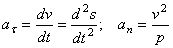 .
.
Итак, мы доказали, что проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) s no времени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю ( ). Эти результаты выражают собою одну из важных теорем кинематики точки.
). Эти результаты выражают собою одну из важных теорем кинематики точки.
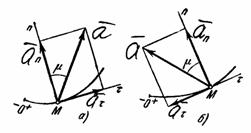
Отложим вдоль касательной  и главной нормали
и главной нормали 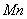 векторы
векторы 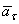 и
и 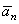 , численно равные
, численно равные 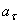 и
и 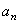 (рис. 9). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая
(рис. 9). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая 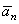 будет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая
будет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая 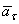 может быть направлена или в положительном, или в отрицательном направлении оси
может быть направлена или в положительном, или в отрицательном направлении оси 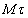 в зависимости от знака проекции
в зависимости от знака проекции 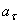 (см. рис.9, а и б).
(см. рис.9, а и б).
Вектор ускорения точки 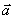 изображается диагональю параллелограмма, построенного на составляющих
изображается диагональю параллелограмма, построенного на составляющих 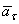 и
и 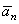 . Так как эти составляющие взаимно перпендикулярны, то по модулю:
. Так как эти составляющие взаимно перпендикулярны, то по модулю:
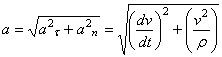 .
.
Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.
1) Прямолинейное движение. Если траекторией точки является прямая линия, то 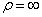 . Тогда
. Тогда 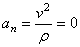 и все ускорение точки равно одному только касательному ускорению:
и все ускорение точки равно одному только касательному ускорению:
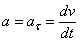 .
.
Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение скорости по численной величине.
2) Равномерное криволинейное движение. Равномерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной: 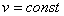 .
.
Тогда 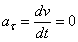 и все ускорение точки равно одному только нормальному:
и все ускорение точки равно одному только нормальному:
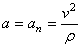 .
.
Вектор ускорения 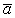 направлен при этом все время по нормали к траектории точки.
направлен при этом все время по нормали к траектории точки.
Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению. Найдем закон равномерного криволинейного движения.
Из формулы 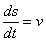 имеем
имеем 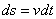 .
.
Пусть в начальный момент (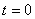 ) точка находится от начала отсчета на расстоянии
) точка находится от начала отсчета на расстоянии 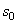 . Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим
. Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим
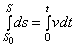 или
или 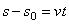 ,
,
так как 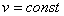 . Окончательно находим закон равномерного криволинейного движения в виде
. Окончательно находим закон равномерного криволинейного движения в виде
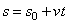 .
.
Если 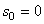 , то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, расчет пропорционального времени, а скорость движения равна отношению пути ко времени
, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, расчет пропорционального времени, а скорость движения равна отношению пути ко времени
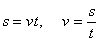 .
.
3) Равномерное прямолинейное движение. В этом случае 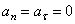 , а значит и
, а значит и 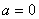 . Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.
. Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.
4) Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: 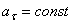 . Найдем закон этого движения, считая, что при
. Найдем закон этого движения, считая, что при 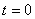 :
: 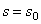 , а
, а 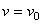 , где
, где 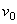 - начальная скорость точки. Согласно формуле
- начальная скорость точки. Согласно формуле 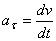 имеем
имеем 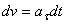 .
.
Так как 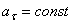 , то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
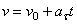 .
.
Формулу представим в виде
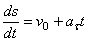 или
или 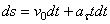 .
.
Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде
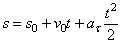 .
.
Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.
Пример 4. Точка движется по окружности радиуса 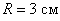 по закону
по закону 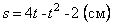 . При
. При 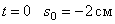 . Значит, движение началось из M 0 (рис.10).
. Значит, движение началось из M 0 (рис.10).
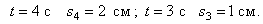
 2014-01-25
2014-01-25 769
769








