Рис.14
Рис.13
Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом 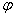 между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол
между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол 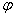 положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси
положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси 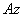 ), и отрицательным, если по ходу часовой стрелки. Измерять угол
), и отрицательным, если по ходу часовой стрелки. Измерять угол 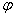 будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла
будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла 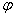 от времени t, т.е.
от времени t, т.е.
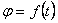 .
.
Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость 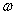 и угловое ускорение
и угловое ускорение 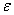 .
.
Если за промежуток времени 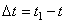 тело совершает поворот на угол
тело совершает поворот на угол 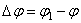 , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет 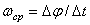 . В пределе при
. В пределе при 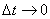 найдем, что
найдем, что
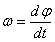 или
или 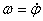 .
.
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак 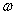 определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,
определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки, 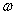 >0, а когда по ходу часовой стрелки, то
>0, а когда по ходу часовой стрелки, то 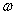 <0.
<0.
Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что тоже, 1/с (с-1), так как радиан - величина безразмерная.
Угловую скорость тела можно изобразить в виде вектора 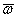 , модуль которого равен |
, модуль которого равен |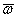 | и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.14). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
| и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.14). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени 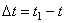 угловая скорость тела изменяется на величину
угловая скорость тела изменяется на величину 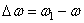 , то числовое значение среднего углового ускорения тела за этот промежуток времени будет
, то числовое значение среднего углового ускорения тела за этот промежуток времени будет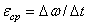 . В пределе при
. В пределе при 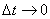 найдем,
найдем,
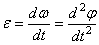 или
или 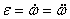 .
.
Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.
Размерность углового ускорения 1/T2 (1/время2); в качестве единицы измерения обычно применяется рад/с2 или, что то же, 1/с2 (с-2).
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Легко видеть, что вращение будет ускоренным, когда величины 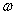 и
и 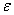 имеют одинаковые знаки, и замедленным, - когда разные.
имеют одинаковые знаки, и замедленным, - когда разные.
Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора 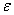 , направленного вдоль оси вращения. При этом
, направленного вдоль оси вращения. При этом
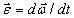 .
.
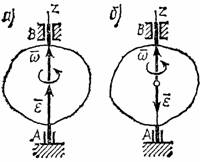
Направление 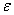 совпадает с направлением
совпадает с направлением 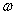 , когда тело вращается ускоренно и (рис.14,а), противоположно
, когда тело вращается ускоренно и (рис.14,а), противоположно 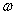 при замедленном вращении (рис.14,б).
при замедленном вращении (рис.14,б).
Если угловая скорость тела остается во все время движения постоянной (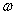 =const), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы
=const), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы 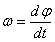 имеем
имеем 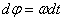 .
.
Отсюда, считая, что в начальный момент времени t =0 угол 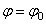 , и беря интегралы слева от
, и беря интегралы слева от 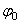 до
до 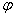 , а справа от 0 до t, получим окончательно
, а справа от 0 до t, получим окончательно
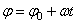 .
.
Из равенства следует, что при равномерном вращении, когда 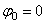
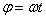 и
и 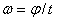 .
.
В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и 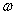 1/с. При одном обороте тело повернется на угол
1/с. При одном обороте тело повернется на угол 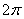 , а при n оборотах на
, а при n оборотах на 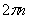 ; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что
; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что
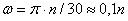 .
.
Если угловое ускорение тела во все время движения остается постоянным 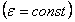 , то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени t =0 угол
, то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени t =0 угол 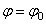 , а угловая скорость
, а угловая скорость 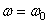 (
(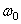 - начальная угловая скорость).
- начальная угловая скорость).
Из формулы 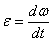 имеем
имеем 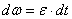 . Интегрируя левую часть в пределах от
. Интегрируя левую часть в пределах от 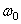 до
до 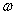 , а правую - в пределах от 0 до t, найдем
, а правую - в пределах от 0 до t, найдем 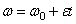 ,
,
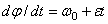 или
или 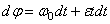 .
.
Вторично интегрируя, найдем отсюда закон равнопеременного вращения
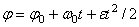 .
.
Если величины 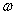 и
и 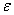 имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
 2014-01-25
2014-01-25 751
751








