2014-01-25
743
 |
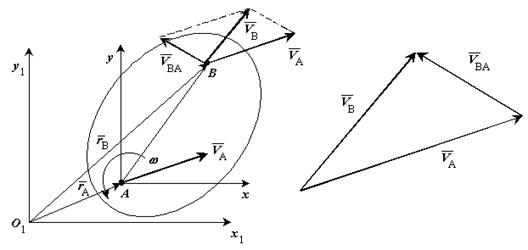
Теорема. Скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса и относительной скорости этой точки от вращения фигуры вокруг полюса.
Рис. 6-5
Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки В фигуры, получаем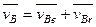 
, где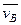 
- абсолютная скорость точки В плоской фигуры; 
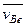- скорость точки В переносного поступательного движения плоской фигуры вместе, например, с точкой А этой фигуры; 
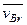- скорость точки B в относительном движении, которым является вращение плоской фигуры вокруг точки А с угловой скоростью w.
Так как за переносное движение выбрано поступательное движение вместе с точкой А, то у всех точек плоской фигуры одинаковые переносные скорости, совпадающие с абсолютной скоростью точки А, т.е.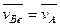 
Скорость относительного движения, в случае когда оно является вращательным движением, равна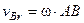 
Скорость 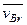расположена в плоскости движущейся фигуры и направлена перпендикулярно отрезку АВ, соединяющему точку В с полюсом А. Эту относительную скорость можно выразить в виде векторного произведения 
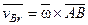, где угловая скорость 
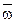считается направленной по подвижной оси вращения, проходящей через точку А и перпендикулярной плоскости фигуры. Относительную скорость 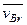обозначим 
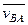. Это обозначение показывает, что скорость относительного движения точки В получается от вращения плоской фигуры вокруг подвижной оси, проходящей через точку А, или просто вокруг точки А.
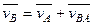, где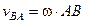 
Что и требовалось доказать.
