Пусть в результате приведения системы сил к заданному центру 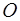 получилось:
получилось:
1. 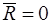 ,
, 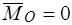 — система находится в равновесии; можно сказать, что она приводится к прямо противоположным силам.
— система находится в равновесии; можно сказать, что она приводится к прямо противоположным силам.
2. 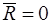 ,
, 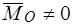 — сила отсутствует, система приводится к паре сил. Выбор полюса приведения не влияет на момент пары сил.
— сила отсутствует, система приводится к паре сил. Выбор полюса приведения не влияет на момент пары сил.
3. 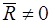 ,
, 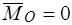 — система приводится к одной силе – равнодействующей.
— система приводится к одной силе – равнодействующей.
4. 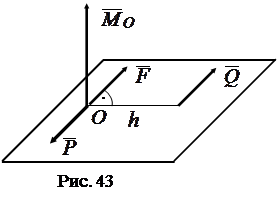
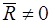 ,
, 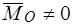 ,
,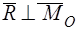
Через точку 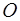 проведем плоскость, перпендикулярную вектору момента
проведем плоскость, перпендикулярную вектору момента 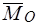 (рис. 43). Приведем систему сил к силе
(рис. 43). Приведем систему сил к силе 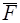 и паре сил
и паре сил 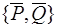 ,
, 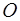 – центр приведения. Сила
– центр приведения. Сила 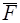 лежит в проведенной плоскости, приложена в центре приведения
лежит в проведенной плоскости, приложена в центре приведения 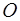 и равна главному вектору:
и равна главному вектору: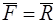 . Пара сил
. Пара сил 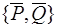
с моментом 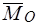 также лежит в проведенной плоскости. Одну из сил пары выберем равной и прямо противоположной силе
также лежит в проведенной плоскости. Одну из сил пары выберем равной и прямо противоположной силе 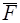 :
: 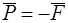 . Другую силу пары
. Другую силу пары 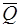 (
(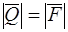 ) проводим так, чтобы момент пары был равен главному моменту системы сил, то есть
) проводим так, чтобы момент пары был равен главному моменту системы сил, то есть 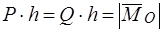 .
.
Полученная система сил 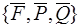 эквивалентна одной силе
эквивалентна одной силе 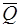 , так как применяя элементарную операцию, прямо противоположные силы
, так как применяя элементарную операцию, прямо противоположные силы 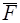 и
и 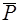 можно отбросить. Система сил приводится к равнодействующей.
можно отбросить. Система сил приводится к равнодействующей.
Общий признак существования равнодействующей
Объединяя частные случаи 2 и 4 можно установить общий признак существования равнодействующей.
Система сил приводится к равнодействующей, если главный вектор не равен нулю, а скалярное произведение главного вектора на главный момент равно нулю:
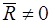 ,
, 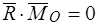 .
.
Действительно, 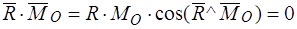 (при
(при 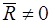 ), если
), если 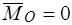 или
или 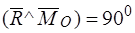 , то есть
, то есть 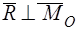 .
.
5. 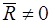 ,
, 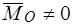 ,
, 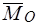 //
//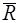 .
.
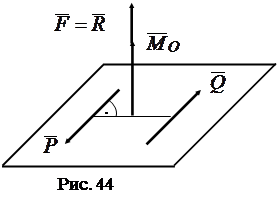 Плоскость пары перпендикулярна векторам силы
Плоскость пары перпендикулярна векторам силы 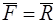 и момента
и момента 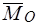 . Таким образом, система эквивалентна силе
. Таким образом, система эквивалентна силе 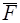 и паре
и паре 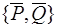 , плоскость которой перпендикулярна силе (рис. 44)
, плоскость которой перпендикулярна силе (рис. 44)
Определение. Совокупность силы и пары сил, которая лежит в плоскости, перпендикулярной этой силе называют динамическим винтом или динамой.
6.
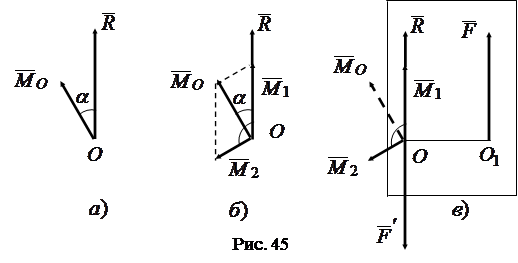 |
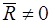 ,
, 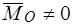 ,
, 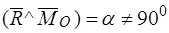 (рис. 45а).
(рис. 45а). Разложим вектор момента 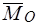 на две составляющие:
на две составляющие: 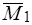 //
//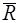 ,
, 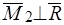 (рис 45б). Через точку
(рис 45б). Через точку 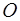 проведем плоскость, перпендикулярную вектору
проведем плоскость, перпендикулярную вектору 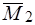 и построим пару
и построим пару 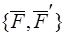 такую, что
такую, что 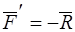 ,
, 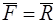 , а момент пары
, а момент пары 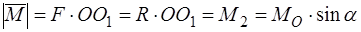 (рис. 45в). Таким образом, сила
(рис. 45в). Таким образом, сила 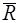 и пара сил с моментом
и пара сил с моментом 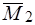 эквивалентны силе
эквивалентны силе 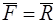 , приложенной в точек
, приложенной в точек 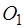 , на расстоянии:
, на расстоянии:
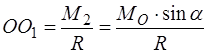 .
.
Следовательно, исходная система сил эквивалентна силе 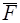 и паре сил с моментом
и паре сил с моментом 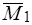 , причем векторы
, причем векторы 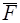 и
и 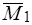 параллельны. Система приводится к динаме.
параллельны. Система приводится к динаме.
Общий признак приведения системы сил к динаме
Объединяя случаи 5 и 6, получим:
Система сил эквивалентна динаме, если скалярное произведение её главного вектора на главный момент не равно нулю:
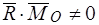 .
.
Теорема Пуансо и частные случаи из нее позволяют привести заданную систему сил к простейшему виду.
Простейшие виды системы сил Условия приведения
1. Прямопротивоположные силы 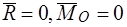 .
.
2. Пара сил 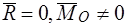 .
.
3. Одна сила (равнодействующая) 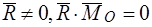 .
.
4. Динама 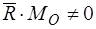 .
.
 2014-01-25
2014-01-25 1422
1422
