2014-01-25
802
Лемма. Если точки приложения параллельных сил расположены в одной плоскости, или лежат на одной прямой, то центр этой системы параллельных сил лежит в этой плоскости или лежит на этой прямой.
Доказательство.
1. Пусть точки приложения системы параллельных сил принадлежат плоскости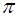 
(рис. 50), которую совместим с координатной плоскостью
.
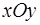Тогда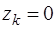 
(
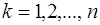). Следовательно, координата центра параллельных
 |
сил
,
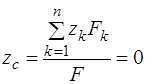то есть центр системы параллельных сил принадлежит плоскости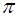
 |
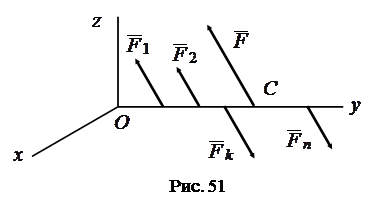2. Пусть точка приложения параллельных сил лежит на прямой
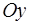(рис. 51)
Тогда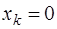 
, 
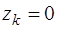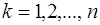(). Вследствие этого 
, 
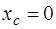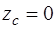. Итак, точка 
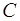лежит на прямой .
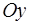Теорема. Если тело имеет плоскость материальной симметрии, либо ось материальной симметрии, либо центр материальной симметрии, то центр тяжести тела лежит в этой плоскости, либо на этой оси, либо в этом центре.
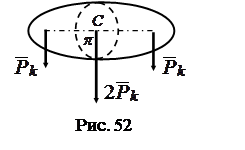Доказательство.
1. Плоскость материальной симметрии (рис. 52).
Пусть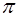 
– плоскость симметрии Центр тяжести каждой пары симметричных частиц лежит в плоскости 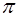. Поэтому можно рассматривать систему параллельных равнодействующих 
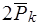, точки приложения которых лежат в плоскости .
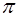Тогда, в соответствии с доказанной леммой, центр тяжести будет лежать в той же плоскости .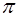
2. Ось материальной симметрии.
 |
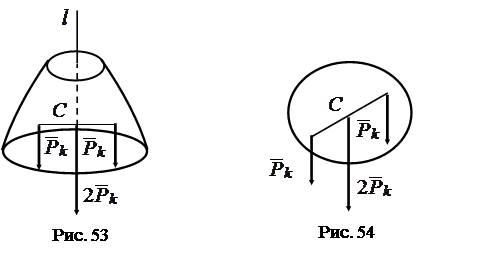Пусть
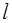– ось материальной симметрии (рис. 53).
Центр тяжести каждой пары материальных частиц будет находиться на оси 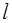. Тогда центр тела принадлежит оси симметрии .
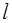3. Центр материальной симметрии.
Пусть 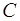– центр материальной симметрии (рис. 54). Равнодействующая каждой пары симметричных частиц будет приложена в центре 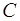. Тогда центр тяжести тела будет лежать в центре материальной симметрии.
Теорема доказана.
