КОНТРОЛЬНА РОБОТА №1
Приклад 1. В партії із 25 деталей є чотири браковані. Знайти ймовірність того, що серед взятих навмання для перевірки п’яти деталей буде дві браковані.
Розв’язання. Розглянемо випадкову подію А – серед п’яти взятих навмання деталей дві браковані. За класичним визначенням ймовірності 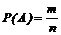 , де n – число всіх рівноможливих елементарних подій в даному випадковому експерименті, m – число елементарних подій, які сприяють події А. Загальне число елементарних подій дорівнює числу способів, за допомогою яких можна вибрати п’ять деталей із 25, тобто
, де n – число всіх рівноможливих елементарних подій в даному випадковому експерименті, m – число елементарних подій, які сприяють події А. Загальне число елементарних подій дорівнює числу способів, за допомогою яких можна вибрати п’ять деталей із 25, тобто 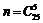 . Дві браковані деталі можна вибрати з чотирьох бракованих
. Дві браковані деталі можна вибрати з чотирьох бракованих 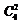 способами, а інші три не браковані –
способами, а інші три не браковані – 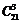 способами. Тоді
способами. Тоді 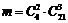 .Отже
.Отже
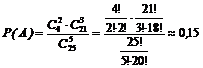 .
.
Приклад 2. Книги деякого чотиритомного видання розставляють навмання на полиці. Знайти ймовірність того, що всі чотири томи стоятимуть в порядку зростання їх номерів.
Розв’язання. Загальне число елементарних подій дорівнює числу переставлень із чотирьох елементів, тобто n =4!=24. Події А сприяє лише одна елементарна подія (1,2,3,4), тобто m =1. Отже 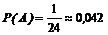 .
.
Приклад 3. В коробці 10 деталей, з яких 8 стандартних. З коробки навмання дістають три деталі. Знайти ймовірність того, що всі три деталі стандартні.
Розв’язання. Подію А (всі три деталі стандартні) представимо як 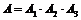 , де події А1,А2,А3 означають, що відповідно перша, друга і третя взяті деталі стандартні. За теоремою про множення ймовірностей
, де події А1,А2,А3 означають, що відповідно перша, друга і третя взяті деталі стандартні. За теоремою про множення ймовірностей
 .
.
Приклад 4. Верстат–автомат штампує деталі. Ймовірність того, що за зміну не буде випущено жодної бракованої деталі, дорівнює 0,9. Знайти ймовірність того, що за три зміни не буде випущено жодної бракованої деталі.
Розв’язання. Подію А (за три зміни не випущено жодної бракованої деталі) представимо, як 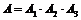 , де події А1, А2, А3 означають, що відповідно за першу, другу і третю зміну не випущено жодної бракованої деталі. Події А1, А2, А3 – незалежні. Тому за теоремою множення ймовірностей:
, де події А1, А2, А3 означають, що відповідно за першу, другу і третю зміну не випущено жодної бракованої деталі. Події А1, А2, А3 – незалежні. Тому за теоремою множення ймовірностей:
Р(А)=Р(А1)× Р(А2) × Р(А3) =0,9 ×0,9 ×0,9 = 0,729.
Приклад 5. На заводі перший цех виробляє 10%, другий – 70%, третій – 20% всіх деталей. В їх продукції браку, відповідно 9, 8, 7%. Знайти ймовірність того, що випадково вибрана деталь дефектна.
Розв’язання. Нехай подія А – деталь дефектна. Висунемо гіпотези: Н1 – деталь виготовлена першим цехом; Н2 – деталь виготовлена другим цехом; Н3 – деталь виготовлена третім цехом. За умовою задачі, відповідні ймовірності 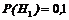 ,
,  ,
, 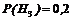 ;
; 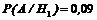 ,
, 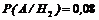 ,
, 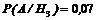 .
.
Застосовуючи формулу повної ймовірності
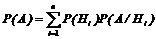 , отримаємо
, отримаємо
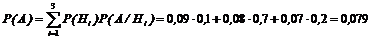 .
.
Приклад 6. На заводі перший цех виробляє 10%, другий – 70%, третій – 20% всіх деталей. В їх продукції браку, відповідно 9, 8, 7%. Випадково вибрана деталь виявилась дефектною. Знайти ймовірність того, що вона виготовлена другим цехом.
Розв’язання. Нехай подія А – деталь дефектна. Висунемо гіпотези: Н1 – деталь виготовлена першим цехом; Н2 – деталь виготовлена другим цехом; Н3 – деталь виготовлена третім цехом. За умовою задачі, відповідні ймовірності 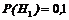 ,
,  ,
, 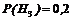 ;
; 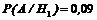 ,
, 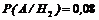 ,
, 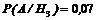 .
.
Застосовуючи формулу Байєса
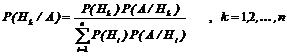 , отримаємо
, отримаємо
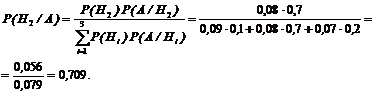
Приклад 7. Проводиться три незалежних випробування, в кожному з яких подія А відбувається з ймовірністю 0,4. Розглядається випадкова величина Х – число появ події А в трьох випробуваннях. Побудувати закон розподілу випадкової величини Х та знайти її математичне сподівання, дисперсію і середнє квадратичне відхилення.
Розв’язання. Випадкова величина Х може набувати значень: 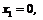
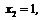

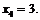 Знайдемо відповідні їм ймовірності. Для цього скористаємося формулою Бернуллі
Знайдемо відповідні їм ймовірності. Для цього скористаємося формулою Бернуллі
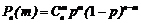 , де
, де 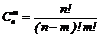 , m= 0, 1, …, n.
, m= 0, 1, …, n.
Отримаємо:
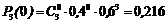 ;
; 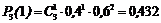 ;
; 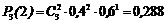 ;
; 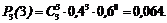
Закон розподілу випадкової величини має вигляд
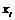 | 0 | 1 | 2 | 3 |
 | 0,216 | 0,432 | 0,288 | 0,064 |
Обчислимо основні числові характеристики випадкової величини:
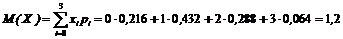 ;
;
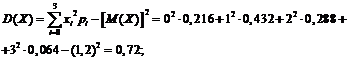
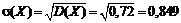 .
.
Приклад 8. Випадкова величина Х задана функцією розподілу
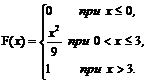
Знайти ймовірність попадання в інтервал (0;1), щільність розподілу, математичне сподівання, дисперсію та середнє квадратичне відхилення. Побудувати графіки функції розподілу та щільності розподілу.
Розв’язання. Ймовірність попадання випадкової величини Х в інтервал (0;1): 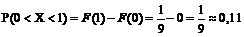 .
.
Оскільки щільність розподілу f(x)=F¢(x), то
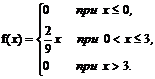
Знайдемо математичне сподівання випадкової величини Х: 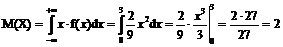 .
.
Визначимо дисперсію випадкової величини Х:
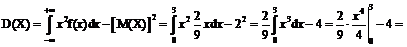
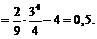
Середнє квадратичне відхилення: 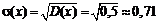 .
.
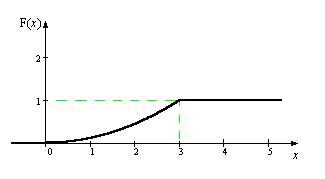
Будуємо графік функції розподілу:
 |
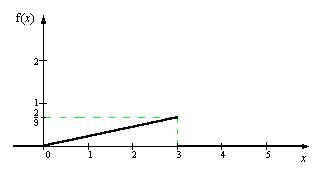
Будуємо графік щільності розподілу:
 |
КОНТРОЛЬНА РОБОТА №2
Приклад 1. Дано вибірку: 1, 3, 4, 5, 1, 3, 4, 3, 5, 1, 3, 4, 1, 3, 4, 3, 4, 3, 4, 3.
Потрібно:
1) побудувати варіаційний ряд;
2) побудувати статистичний розподіл вибірки;
3) побудувати полігон відносних частот;
4) знайти емпіричну функцію розподілу і побудувати її графік.
Розв’язання.
1) Побудуємо варіаційний ряд
1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5.
2) Порахуємо частоти з якими варіанти xi входять у вибірку та запишемо статистичний розподіл вибірки:
| xi | 1 | 3 | 4 | 5 |
| n i | 4 | 8 | 6 | 2 |
3) Знайдемо відносні частоти. Оскільки об’єм вибірки n =4+8+6+2=20, то w 1 =4/20=0,2; w 2 =8/20=0,4; w 3 =6/20=0,3; w 4 =2/20=0,1.
Отже розподіл відносних частот має вигляд:
| xі | 1 | 3 | 4 | 5 |
| w і | 0,2 | 0,4 | 0,3 | 0,1 |
На площині (хі; w і) зобразимо точки з координатами (1;0,2), (3;0,4), (4;0,3), (5;0,1) та з’єднаємо їх відрізками. Отримаємо шуканий полігон відносних частот.
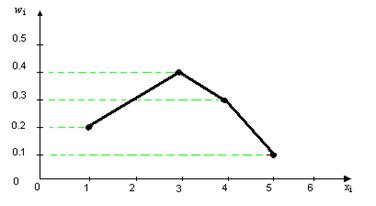 |
4) Емпіричну функцію розподілу
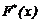 знаходимо за формулою:
знаходимо за формулою: 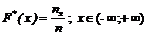 , де
, де 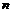 – об’єм вибірки;
– об’єм вибірки; 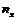 - число варіант, які менші
- число варіант, які менші  . В даній задачі
. В даній задачі 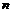 = 20.
= 20.
При 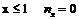 , оскільки найменша варіанта х1=1. Тому
, оскільки найменша варіанта х1=1. Тому 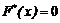 , при
, при 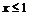 .
.
При 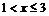 лише варіанта х1=1< х, причому
лише варіанта х1=1< х, причому 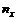 =4. Тому
=4. Тому 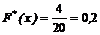 , при
, при 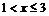 .
.
При 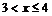 варіанти х1 =1 і х2 =3 менші х, причому
варіанти х1 =1 і х2 =3 менші х, причому 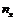 =4+8=12. Тому
=4+8=12. Тому 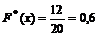 при
при 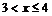 .
.
При 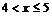 варіанти х1 =1, х2 =2 і х3 =4 менші х, причому
варіанти х1 =1, х2 =2 і х3 =4 менші х, причому 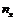 =4+8+6=18. Тому
=4+8+6=18. Тому 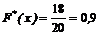 при
при 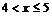 .
.
При x >5 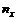 =20 і отже
=20 і отже 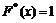 .
.
Таким чином емпірична функція розподілу має вигляд:
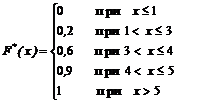 .
.
Будуємо графік цієї функції.
 |
Приклад 2. Дано інтервальний варіаційний ряд
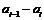 | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 |
| n i | 7 | 10 | 20 | 8 | 5 |
Побудувати гістограму відносних частот.
Розв’язання. Об’єм вибірки 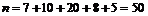 , довжина часткового інтервалу h =2.
, довжина часткового інтервалу h =2.
Знаходимо щільності відносних частот w i за формулою 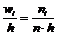 :
:
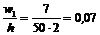 ;
; 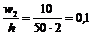 ;
; 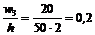 ;
; 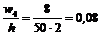 ;
; 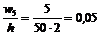 .
.
Відкладемо на осі абсцис часткові інтервали 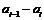 і проведемо над цими інтервалами відрізки, які паралельні осі абсцис і знаходяться від неї на відстанях рівних відповідно w i / h. Отримаємо шукану гістограму відносних частот.
і проведемо над цими інтервалами відрізки, які паралельні осі абсцис і знаходяться від неї на відстанях рівних відповідно w i / h. Отримаємо шукану гістограму відносних частот.
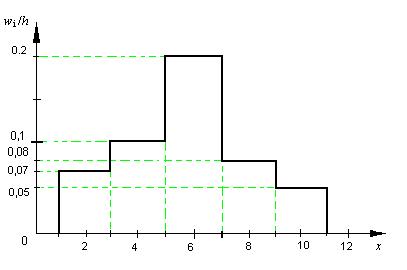 |
Приклад 3.
1) Задано статистичний розподіл вибірки
| x i | 1 | 2 | 5 | 6 |
| n i | 2 | 3 | 4 | 1 |
Знайти вибіркове середнє 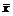 , вибіркову дисперсію
, вибіркову дисперсію 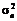 , виправлену вибіркову дисперсію
, виправлену вибіркову дисперсію 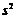 і вибіркове середнє квадратичне відхилення
і вибіркове середнє квадратичне відхилення 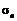 .
.
2) Задано інтервальний варіаційний ряд
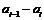 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| n i | 42 | 73 | 154 | 205 | 26 |
Знайти вибіркове середнє 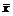 та вибіркову дисперсію
та вибіркову дисперсію 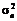 .
.
Розв’язання. 1) Об’єм вибірки n =2+3+4+1=10.
Вибіркове середнє 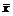 знаходимо за формулою:
знаходимо за формулою: 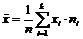 .
.
Отримаємо: 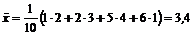 .
.
Вибіркову дисперсію знаходимо за формулою:
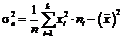 .
.
Отримаємо: 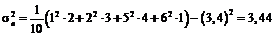 .
.
Знаходимо 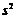 та
та 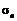 :
: 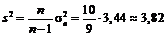 ,
,
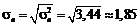 .
.
2) Знаходимо середини часткових інтервалів: х 1=3, х 2=5, х 3=7, х 4=9, х 5=11. За формулами отримаємо: 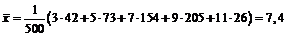 ;
;
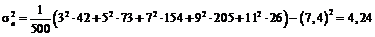 .
.
Приклад 4. Побудувати надійний інтервал для оцінки з надійністю 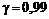 невідомого математичного сподівання
невідомого математичного сподівання 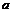 нормально розподіленої генеральної сукупності Х, якщо
нормально розподіленої генеральної сукупності Х, якщо 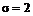 ,
, 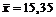 і
і 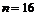 .
.
Розв’язання. Шуканий надійний інтервал має вигляд
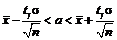 , , | (1) |
де 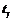 – значення аргументу функції Лапласа
– значення аргументу функції Лапласа 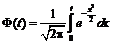 , при якому
, при якому 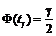 . Знаходимо
. Знаходимо 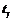 із співвідношення
із співвідношення 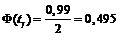 .
.
За таблицею значень функції Лапласа знаходимо  . Підставляючи
. Підставляючи 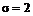 ,
, 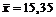 ,
, 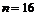 ,
,  в (1), отримаємо надійний інтервал: 14,06 <
в (1), отримаємо надійний інтервал: 14,06 < 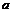 < 16,64.
< 16,64. 
Приклад 5. Побудувати надійний інтервал для оцінки з надійністю 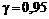 невідомого середнього квадратичного відхилення
невідомого середнього квадратичного відхилення 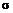 нормально розподіленої генеральної сукупності Х, якщо
нормально розподіленої генеральної сукупності Х, якщо 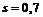 і
і 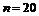 .
.
Розв’язання. Шуканий надійний інтервал має вигляд:
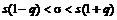 , при q <1; , при q <1; 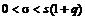 , при q ³1; , при q ³1; | (2) |
де 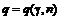 знаходиться за таблицею по заданих
знаходиться за таблицею по заданих 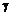 і
і 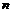 . При
. При 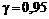 і
і 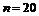 за таблицею знаходимо q =0,37.
за таблицею знаходимо q =0,37.
Підставляючи 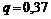 ,
, 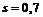 ,
, 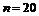 в (2), отримаємо надійний інтервал: 0,441
в (2), отримаємо надійний інтервал: 0,441 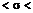 0,959.
0,959.
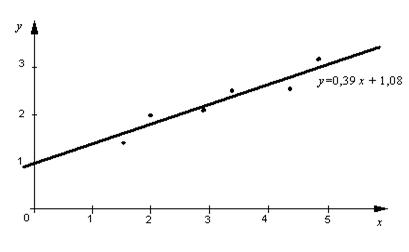
Приклад 6. Знайти вибіркове рівняння прямої регресії 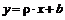 за даними шести спостережень (xi ; yi): (1,5;1,3), (2;2), (3;2,1), (3,5;2,7), (4,5;2,6), (5;3,3). Зробити малюнок, на якому вказати експериментальні дані та побудувати пряму регресії.
за даними шести спостережень (xi ; yi): (1,5;1,3), (2;2), (3;2,1), (3,5;2,7), (4,5;2,6), (5;3,3). Зробити малюнок, на якому вказати експериментальні дані та побудувати пряму регресії.
Розв’язання. Невідомі параметри регресії 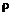 і b знаходять із системи рівнянь
і b знаходять із системи рівнянь
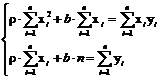 . . | (3) |
З умови задачі знаходимо: 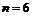 ,
, 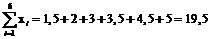 ,
, 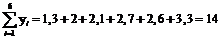 ,
, 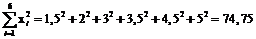 ,
, 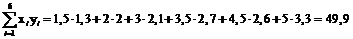 ,
,
Підставляючи в (3), отримаємо систему:
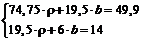 .
.
Звідки, розв’язуючи систему, отримаємо 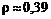 і
і 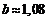 .
.
Запишемо шукане рівняння прямої лінії регресії:
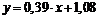 .
.
Зробимо малюнок, на якому вкажемо експериментальні дані та побудуємо пряму лінію регресії.
 |
Приклад 7. Використовуючи критерій Пірсона, при рівні значущості 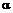 перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х з статистичними даними, які подані у вигляді інтервального варіаційного ряду (в першому рядку вказано часткові інтервали
перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х з статистичними даними, які подані у вигляді інтервального варіаційного ряду (в першому рядку вказано часткові інтервали 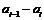 , в другому – відповідні їм частоти
, в другому – відповідні їм частоти 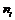 ).
).
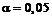 ;
;
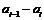 | –20-(–10) | –10-0 | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
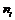 | 20 | 47 | 80 | 89 | 40 | 16 | 8 |
Розв’язання. Знайдемо середини часткових інтервалів 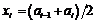 та складемо таблицю
та складемо таблицю
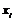 | –15 | –5 | 5 | 15 | 25 | 35 | 45 |
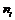 | 20 | 47 | 80 | 89 | 40 | 16 | 8 |
Обчислимо вибіркове середнє 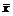 та вибіркове середнє квадратичне відхилення
та вибіркове середнє квадратичне відхилення 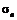 (див. приклад 3, КР № 2.):
(див. приклад 3, КР № 2.):
об’єм вибірки 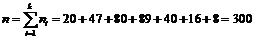 ;
;
вибіркове середнє 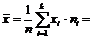
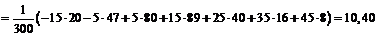 ;
;
вибіркова дисперсія 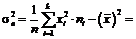
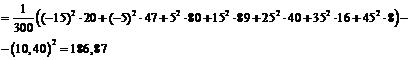 і вибіркове середнє квадратичне відхилення
і вибіркове середнє квадратичне відхилення 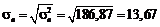 .
.
Перейдемо до випадкової величини 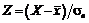 та обчислимо кінці інтервалів
та обчислимо кінці інтервалів 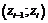 :
: 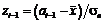 ;
; 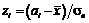 , причому найменше значення
, причому найменше значення 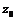 покладемо рівним
покладемо рівним 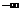 , а найбільше значення
, а найбільше значення  покладемо рівним
покладемо рівним 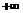 .
.
Обчислимо теоретичні ймовірності  потрапляння випадкової величини
потрапляння випадкової величини  в інтервали
в інтервали 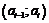 за формулою
за формулою 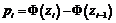 , де
, де 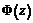 – функція Лапласа, та теоретичні частоти
– функція Лапласа, та теоретичні частоти 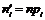 (тут
(тут 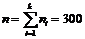 – об’єм вибірки). Для цього заповнимо розрахункову таблицю:
– об’єм вибірки). Для цього заповнимо розрахункову таблицю:
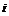 | 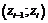 | 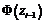 | 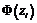 |  | 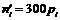 |
| 1 | 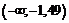 | –0,5000 | –0,4319 | 0,0681 | 20,43 |
| 2 | 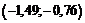 | –0,4319 | –0,2764 | 0,1555 | 46,65 |
| 3 | 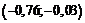 | –0,2764 | –0,0120 | 0,2644 | 79,32 |
| 4 |  | –0,0120 | 0,2580 | 0,2700 | 81,00 |
| 5 | 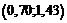 | 0,258 | 0,4236 | 0,1656 | 49,68 |
| 6 | 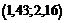 | 0,4236 | 0,4846 | 0,0610 | 18,30 |
| 7 | 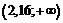 | 0,4846 | 0,5000 | 0,0154 | 4,62 |
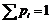 | 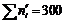 |
Обчислимо вибіркове значення критерію 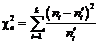 . Для цього заповнимо наступну розрахункову таблицю:
. Для цього заповнимо наступну розрахункову таблицю:
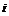 | 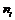 | 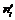 |  | 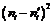 | 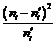 |
| 1 | 20 | 20,43 | –0,43 | 0,1849 | 0,0091 |
| 2 | 47 | 46,65 | 0,35 | 0,1225 | 0,0026 |
| 3 | 80 | 79,32 | 0,68 | 0,4624 | 0,0058 |
| 4 | 89 | 81,00 | 8,00 | 64,0000 | 0,7901 |
| 5 | 40 | 49,68 | –9,68 | 93,7024 | 1,8861 |
| 6 | 16 | 18,30 | –2,30 | 5,2900 | 0,2891 |
| 7 | 8 | 4,62 | 3,38 | 11,4244 | 2,4728 |
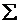 | 300 | 300 | 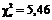 |
За таблицею критичних точок розподілу 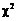 по рівню значущості
по рівню значущості 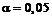 та числу ступенів свободи
та числу ступенів свободи 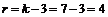 знаходимо критичну точку правосторонньої критичної області
знаходимо критичну точку правосторонньої критичної області 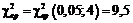 .
.
Оскільки  , то немає підстав відхилити нульову гіпотезу. Отже, статистичні дані узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.
, то немає підстав відхилити нульову гіпотезу. Отже, статистичні дані узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.
ДОДАТКИ
Таблиця значень функції 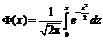
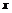 | 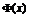 | 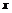 | 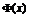 | 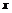 | 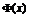 | 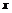 | 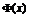 | 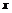 | 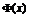 |
| 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50 0,51 | 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879 0,1915 0,1950 | 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 | 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2517 0,2549 0,2580 0,2611 0,2642 0,2673 0,2704 0,2734 0,2764 0,2794 0,2823 0,2852 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133 0,3159 0,3186 0,3212 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389 0,3413 0,3438 0,3461 0,3485 | 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 | 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830 0,3849 0,3869 0,3888 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 | 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 1,78 1,79 1,80 1,81 1,82 1,83 1,84 1,85 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 | 0,4406 0,4418 0,4429 0,4441 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545 0,4554 0,4564 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 0,4625 0,4633 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 0,4699 0,4706 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767 0,4772 0,4783 0,4793 0,4803 0,4812 0,4821 0,4830 0,4838 | 2,16 2,18 2,20 2,22 2,24 2,26 2,28 2,30 2,32 2,34 2,36 2,38 2,40 2,42 2,44 2,46 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66 2,68 2,70 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90 2,92 2,94 2,96 2,98 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00 | 0,4846 0,4854 0,4861 0,4868 0,4875 0,4881 0,4887 0,4893 0,4898 0,4904 0,4909 0,4913 0,4918 0,4922 0,4927 0,4931 0,4934 0,4938 0,4941 0,4945 0,4948 0,4951 0,4953 0,4956 0,4959 0,4961 0,4963 0,4965 0,4967 0,4969 0,4971 0,4973 0,4974 0,4976 0,4977 0,4979 0,4980 0,4981 0,4982 0,4984 0,4985 0,4986 0,49865 0,49931 0,49966 0,499841 0,499928 0,499968 0,499997 0,499997 |
Таблиця значень функції 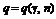
|
|
| ||
| 0,95 | 0,99 | 0,999 | |
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 45 50 60 70 80 90 | 1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39 0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 | 2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60 0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 | 5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92 0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 |
Критичні точки розподілу 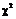
| Число ступенів свободи | Рівень значущості | ||
| 0,01 | 0,025 | 0,05 | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | 6,6 9,2 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7 29,1 30,6 32,0 33,4 34,8 36,2 37,6 38,9 40,3 41,6 43,0 44,3 | 5,0 7,4 9,4 11,1 12,8 14,4 16,0 17,5 19,0 20,5 21,9 23,3 24,7 26,1 27,5 28,8 30,2 31,5 32,9 34,2 35,5 36,8 38,1 39,4 40,6 | 3,8 6,0 7,8 9,5 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4 23,7 25,0 26,3 27,6 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 |
ЗМІСТ
Варіанти завдань контрольних робіт.............................................................. 3
Контрольна робота №1.................................................................................... 3
Контрольна робота №2................................................................................. 20
Приклади розв’язування задач........................................................................ 29
Контрольна робота №1.................................................................................. 29
Контрольна робота №2.................................................................................. 33
Додатки.................................................................................................................. 43
 2018-02-13
2018-02-13 1429
1429