Розглянемо спрямлювану криву 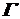 , в кожній точці якої задано функцію
, в кожній точці якої задано функцію 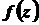 . Інтегралом від функції
. Інтегралом від функції 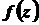 вздовж
вздовж 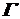 називають
називають
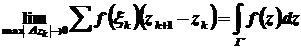 ,
,
де криву поділено на малі частки 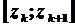 ,
, 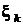 – довільна точка, яка лежить на відповідній частці кривої, а границя існує і не залежить від способу поділу кривої на частки та від способу вибору точок
– довільна точка, яка лежить на відповідній частці кривої, а границя існує і не залежить від способу поділу кривої на частки та від способу вибору точок 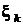 .
.
Якщо 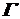 є кусочно гладкою кривою, а функція
є кусочно гладкою кривою, а функція 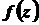 – кусочно неперервна та обмежена, то цей інтеграл завжди існує. Він зводиться до обчислення вздовж кривої
– кусочно неперервна та обмежена, то цей інтеграл завжди існує. Він зводиться до обчислення вздовж кривої 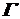 криволінійних інтегралів за координатами від функцій дійсних змінних
криволінійних інтегралів за координатами від функцій дійсних змінних
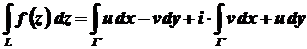 .
.
Теорема Коші. Якщо функція 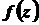 аналітична у однозв’язній області
аналітична у однозв’язній області 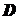 , межею якої є кусочно гладкий контур
, межею якої є кусочно гладкий контур 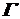 , та неперервна у замкненій області
, та неперервна у замкненій області 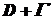 , то інтеграл від цієї функції вздовж лінії
, то інтеграл від цієї функції вздовж лінії 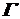 дорівнює нулю:
дорівнює нулю:
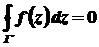 .
.
Теорема Коші для багатозв’язної області. Розглянемо область 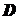 , межа якої
, межа якої 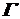 складається з замкненої лінії
складається з замкненої лінії 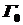 та ліній
та ліній 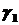 ,
, 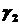 ,…
,… 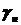 , які лежать всередині
, які лежать всередині 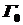 та попарно не перетинаються. Тоді, якщо функція
та попарно не перетинаються. Тоді, якщо функція 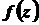 аналітична у області
аналітична у області 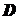 та неперервна у замкненій області
та неперервна у замкненій області 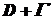 , то інтеграл від цієї функції вздовж повного контуру
, то інтеграл від цієї функції вздовж повного контуру 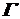 дорівнює нулю:
дорівнює нулю:
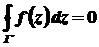 , тобто
, тобто
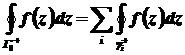 .
.
Інтегральна формула Коші. Розглянемо однозв’язну область 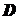 та замкнену криву
та замкнену криву 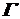 , яка повністю міститься у
, яка повністю міститься у 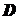 разом з своєю внутрішністю
разом з своєю внутрішністю 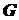 . Якщо функція
. Якщо функція 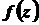 аналітична у області
аналітична у області 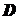 , то для будь-якої точки
, то для будь-якої точки 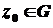 має місце рівність
має місце рівність
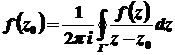 .
.
Інтеграл 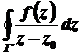 називається інтегралом Коші.
називається інтегралом Коші.
Формула типу Коші. Якщо функція 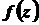 аналітична у області
аналітична у області 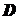 та неперервна у замкненій області
та неперервна у замкненій області 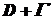 , то у довільній внутрішній точці області
, то у довільній внутрішній точці області 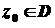 функція
функція 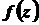 має похідну будь-якого порядку, та
має похідну будь-якого порядку, та
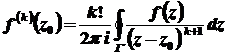 .
.
Ряди з комплексними членами.
 2018-02-13
2018-02-13 172
172







