2018-03-09
72
Для вычисления yi и yi+1 по формулам (8) и (9) необходимо пользоваться схемой, приведенной в следующей таблице 2:
| i | x | y | f(x,y) | К=hf(x,y) | ∆у |
| 0 | x0 | y0 | f(x0,y0) | К1(0) | К1(0) |
x0 +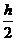 
| y0+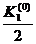 
| f(x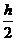0+ ,y0+ )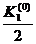
| К2(0) | 2К2(0) | |
| x0 +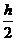
| y0+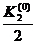 
| f(x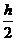0+ ,y0+ )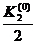
| К3(0) | 2К3(0) | |
| x0 + h | y0+K3(0) | f(x0 + h, y0+K3(0)) | К4(0) | 2К4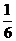(0) | |
 ∑=∆у0
| |||||
| 1 | x1 | y1 | f(x1,y1) | К1(2) | К1(2) |
Порядок заполнения таблицы.
В первой строке таблицы:
1) записываем начальные данные x0, y0;
2) вычисляем f(x0,y0) и умножаем на h, полученное значение К1(0) заносим в столбец значений K
Во второй строке таблицы:
3) записываем x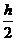0 + , y0+ ;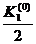
4) вычисляем f(x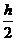0+ ,y0+ 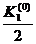), умножаем на h и заносим в таблицу полученное К2(0).
В третьей строке таблицы:
5) записываем x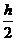0 + , y0+ ;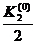
6) вычисляем f(x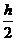0+ ,y0+ 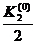), умножаем на h и записываем так найденное К3(0) .
В четвертой строке таблицы:
7) записываем x0 + h, y0+K3(0) ;
8) вычисляем f(x0 + h, y0+K3(0)), это значение, умноженное на h, определяет К4(0) ;
9) в столбце ∆у выписываются построчно значения К1(0) , 2К2(0) , 2К3(0) , К4(0) , которые суммируются. Сумма, разделенная на 6, определяет ∆у0;
|
|
|
10) вычисляем у1 =у0 +∆у0 .
Затем вычисления повторяются в том же порядке для точки (x1,y1).
Пример 3. Используя метод Рунге – Кутта, найти приближенное решение уравнения y´=x+y при условии y(0)=1 на отрезке [0;0,3], приняв шаг h=0,1. Вычисления вести с четырьмя десятичными знаками.
Решение. Покажем начало вычислительного процесса.
Для определения у1 вычислим К1(0), К2(0) , К3(0) , К4(0) .
f(x0,y0)= f(0,1) = 0+1=1
К1(0) = h f(x0,y0) = 0,1·1=0,1
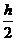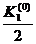f(x0+ ,y0+ ) =f(0;0,5;1,05) = 0,05+1,05=1,1
К2(0) = h f(x0+ 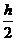,y0+ 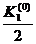) = 0,1·1,1=0,11
f(x0+ 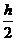,y0+ 
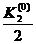) = f(0,05;1,055) =1,105
К3(0) = h f(x0+ 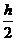,y0+ 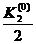) = 0,1·1,105=0,1105
f(x0 + h, y0+K3(0)) = f(0,1;1,055) = 0,1·1,105=1,2105
К4(0) = h f(x0+ 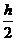, y0+K3(0)) = 0,1·1,2105=0,1211
Отсюда
∆у0 = 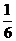(0,1+2·0,11+2·0,1105+0,1211) =0,1103
и, следовательно,
у1 =у0 +∆у0 =1 + 0,1103 =1,1103
Пример 4. Используя метод Рунге – Кутта, решить пример 1. Вычисления вести с точностью до четырех десятичных знаков.
Решение. Воспользуемся таблицей из примера 1. Имеем y0 =1, f(x0,y0)=0, y1(1) =1, f(x1,y1 (1))=0,5∙0,1∙1=0,05. По формуле (7) получим
у1(2) = y0 + ½[ f(x0, y0 )+ f(x1,y1 (1) )]h=1+0,5(0+0,05)0,1=1,0025.
Вычисляем f(x1,y1 (2) )=0,5∙0,1∙1,0025=0,0501. Тогда по формуле (7) находим
у1(3) = y0 + ½[ f(x0, y0 )+ f(x1,y1 (2) )]h=1+0,5(0+0,0501)0,1=1,0025.
Таким образом, с точностью до четырех десятичных знаков у1(2) = у1(3) = 1,0025= у1 и т.д. Результаты вычислений заносим в следующую таблицу 3:
| k | xk | yk | f(xk,yk) | f(xk,yk)h | e x²/4 |
| 0 | 0 | y0 =1 | 0 | 0 | 1 |
| 1 | 0,1 | y1(2) = у1(3) = y1 =1,0025 | 0,0501 | 0,0050 | 1,0025 |
| 2 | 0,2 | y2(1) = y2(2)= y2 = 1,0100 | 0,1010 | 0,0101 | 1,0100 |
| 3 | 0,3 | y3(1)= y3(2)= y3 = 1,0227 | 0,1534 | 0,0153 | 1,0227 |
| 4 | 0,4 | y4(3)= y4(4)= y4 = 1,0408 | 0,2082 | 0,0208 | 1,0408 |
| 5 | 0,5 | y5(2)= y5(3)= y5 = 1,0646 | 0,2661 | 0,0266 | 1,0645 |
| 6 | 0,6 | y6(2)= y6(3)= y6 = 1,0943 | 0,3283 | 0,0328 | 1,0942 |
| 7 | 0,7 | y7(2)= y7(3)= y7 = 1,1305 | 0,3957 | 0,0396 | 1,1303 |
| 8 | 0,8 | y8(2)= y8(3)= y8 = 1,1738 | 0,4695 | 0,0470 | 1,1735 |
| 9 | 0,9 | y9(2)= y9(3)= y9 = 1,2248 | 0,5512 | 0,0551 | 1,2244 |
| 10 | 1,0 | y10(3)= y10(4)= y10 =1,2845 | 1,2840 |
|
|
|
В данном случае можно найти точное решение уравнения, имеющее вид у = e x²/4 (значения этой функции помещены в последнем столбце таблицы). Сравнивая значения yk в таблицах 1 и 3 со значениями функции у = e x²/4 , заключаем, что метод Рунге-Кутта позволяет получить лучшие результаты, чем метод Эйлера. Можно показать, что метод Рунге-Кутта дает на каждом шаге погрешность, порядок которой не превышает h3, поэтому он нередко применяется в вычислительной практике.
Лабораторные задания
Задание 1. Используя метод Эйлера, составить таблицу приближенных значений частного решения уравненияудовлетворяющего начальному условию:
1) y´=x+y на отрезке [0;0,5], y(0)=1, h=0,1
2) y´=x+y на отрезке [-1;0], y(-1)=0, h=0,1
3) y´=2x-y² на отрезке [0;1], y(0)=0, h=0,1
4) y´=y³-x на отрезке [0;2], y(0)=1, h=0,1
5) y´- 0,1y² = x·y на отрезке [1;2], y(1)=0, h=0,1
6) y´= 
на отрезке [1;4], y(1)=1, h=0,1
7) y´=1/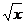 
на отрезке [1;5], y(1)=0, h=0,1
8)y´=1/x² на отрезке [2;4], y(2)=1, h=0,1
9) y´=1/x³ на отрезке [2;4], y(2)=-2, h=0,1
10) y´=1/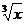 
на отрезке [3;5], y(3)=2, h=0,1
11) y´= - 1/ 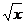на отрезке [1;5], y(1)=-1, h=0,1
12) y´=10/x на отрезке [5;3], y(5)=-1, h=0,1
13) y´= - 10/x на отрезке [5;4], y(5)=0, h=0,1
14) y´=1/x³ на отрезке [1;5], y(1)=-1, h=0,1
15) y´=1/ 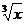на отрезке [5;1], y(5)=-1, h=0,1
16) y´= - 1/x³ на отрезке [4;2], y(4)=0, h=0,1
17) y´= - 1/ 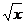на отрезке [5;3], y(5)=-2, h=0,1
18) y´= - на отрезке [1;5], y(1)=2, h=0,1
19) y´= - 10/x на отрезке [5;1], y(5)=2, h=0,1
20) y´=1/ 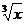на отрезке [1;5], y(1)=0, h=0,1
21) y´=1/x³ на отрезке [1;2], y(1)=0, h=0,1
22) y´=1/x² на отрезке [5;4], y(5)=2, h=0,1
23) y´= 1/ 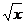на отрезке [2;4], y(2)=1, h=0,1
24) y´= - на отрезке [5;3], y(5)=0, h=0,1
25) y´= - 1/x³ на отрезке [3;4], y(3)=1, h=0,1
26) y´= 1/ 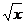на отрезке [5;1], y(5)=-2, h=0,1
27) y´= на отрезке [2;4], y(2)=2, h=0,1
28) y´=1/x² на отрезке [3;5], y(3)=-2, h=0,1
29) y´=y²-x² на отрезке [1;2], y(1)=1, h=0,1
30) y´=y³-x на отрезке [0;2], y(0)=1, h=0,1
Задание 2. Используя метод Рунге – Кутта, составить таблицу приближенных значений решения дифференциального уравнения y´= f(x,y) на отрезке [0;0,5] (примеры с 1 по 16), на отрезке [0;1] (примеры при с 17 по 26), на отрезке [1;2] (примеры с 27 по 30) начальном условии y(x0)=y0 с точностью 0,001 шаг h=0,1.
| № | y(x0)=y0 | y´=f(x,y) | № | y(x0)=y0 | y´=f(x,y) |
| 1 | y(0)=0,5 | y´=x+y² | 16 | y(0)=1 | y´=y²+x+1 |
| 2 | y(0)=0,2 | y´=2x+0,1y | 17 | y(0)=0 | y´=xy³+ x² |
| 3 | y(0)=0,3 | y´=2x+y² | 18 | y(0)=0 | y´=xy³-1 |
| 4 | y(0)=0,2 | y´=x²+xy | 19 | y(0)=1 | y´= x²y²-1 |
| 5 | y(0)=0,1 | y´=0,2x+y² | 20 | y(0)=0 | y=siny-sinx |
| 6 | y(0)=0,4 | y´=x²+y | 21 | y(0)=1 | y´=  +0,5y
|
| 7 | y(0)=0,1 | y´=x²+2y | 22 | y(0)=1 | y´=y³- x |
| 8 | y(0)=0,6 | y´=xy+y² | 23 | y(0)=1,5 | y´= y-x |
| 9 | y(0)=0,7 | y´=x²+ y² | 24 | y(0)=0 | y´=2x-y² |
| 10 | y(0)=0,2 | y´=x²+0,2y² | 25 | y(0)=0 | y´=x²+0,3y²+1 |
| 11 | y(0)=0,4 | y´=0,3x+y² | 26 | y(0)=1 | y´=- 0,2xy² |
| 12 | y(0)=0,3 | y´=0,1x+0,2y² | 27 | y(1)=0 | y´- 0,1y² = xy |
| 13 | y(0)=0,5 | y´=x+0,3y² | 28 | y(1)=0 | y´=1/x³ |
| 14 | y(0)=0,5 | y´=2x²+xy | 29 | y(1)=1 | y´=y²-x² |
| 15 | y(0)=0,8 | y´=0,1x²+2xy | 30 | y(1)=1 | y´=y / x- y² |
Список используемой литературы
1. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч 2. – М.: высшая школа, 1998. – 415 с.
2. Шестаков А. А., Малышева И. А., Полозков Д. П. Курс математики: Учебное пособие для студентов втузов. – М.: высшая школа, 1987. – 320 с.
3. Задачи и упражнения по математическому анализу для втузов: Учебное пособие для студентов высших технических учебных заведений. Г. С. Бараненков, Б. П. Демидович, В. А. Ефименко и др.; Под ред. Б. П. Демидовича. – М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2002. – 495 с.
4. Ильин В. А., Позняк Э. Г. Основы математического анализа: Учебник для вузов: 4.1. – 5-е изд. – М.: Наука, ФИЗМАТЛИТ, 2000. – 616 с.
5. Пискунов Н. С. Дифференциальное и интегральное исчисления, Т. 2. – М.: Интеграл – Пресс, 2002. –
|
|
|
6. Практикум по обыкновенным дифференциальным уравнениям. – Уфа, Изд-во УГНТУ, 2000. – 48 с.
Содержание
1.Методические указания…………………………………………1
2.Лабораторные задания…………………………………………..9
3.Список используемой литературы……………………………..11
