Метод Рунге – Кутта (метод Эйлера с уравнением)

Метод Эйлера очень прост для вычислений, но имеет недостаток: при значительном изменении х приближенные значения у могут сильно отличаться от точных, так как погрешность накапливается с каждым шагом (рис.1). Значительно лучшие результаты можно получить, применив в методе Эйлера уравнение, состоящее в следующем. Обозначим значение y_k,вычисленное по формуле (6), через y_k⁽¹⁾ и уточним это значение по формуле

           y_k⁽²⁾ = y_k-1 + ½[ f(x_k-1, y_k-1 )+ f(x_k,y_k ⁽¹⁾ )]h            (7)          

           Найденное значение снова можно уточнить по аналогичной соотношению (7) формуле

           y_k⁽³⁾ = y_k-1 + ½[ f(x_k-1, y_k-1 )+ f(x_k,y_k ⁽²⁾ )]h

и т.д. Этот процесс продолжаем до тех пор, пока в пределах заданной точности не совпадут результаты двух последовательных вычислений. Затем тем же методом вычисляем y_k+1 и т.д.

В методе Рунге – Кутта до четвертого порядка точности ограничиваются пятью членами разложения(удерживаются члены до h⁴ включительно).Тогда вычисление приближенного значения y_i+1 производится по формуле

 y_i+1 = y_i + 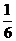(К₁⁽ⁱ⁾+2К₂⁽ⁱ⁾+2К₃⁽ⁱ⁾+К₄⁽ⁱ⁾)        (8)

К₁⁽ⁱ⁾ = h f(x_i,y_i), К₂⁽ⁱ⁾= h f(x_i + 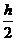,y_i + К₁⁽ⁱ⁾ /2 ).

К₃⁽ⁱ⁾= h f(x_i + 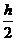,y_i + К₂⁽ⁱ⁾ /2 ),

К₄⁽ⁱ⁾= h f(x_i +h,y_i + К₃⁽ⁱ⁾ )               (9)