Множества и отображения

Если каждому элементу m некоторого множества Мпо какому-нибудь правилу сопоставляется элемент j(m), то это сопоставление j называется функцией.

Если все объекты j(m) принадлежат некоторому множеству N, то сопоставление m— >j(m) называется также отображением из М в N. Элемент j(m) называется образом элемента m, а m называется прообразом элемента j(m). Образ j(m) определяется элементом m однозначно, но m не обязательно однозначно определяется элементом j(m).

Определение. Отображение множества Мв множество Nназывается сюръективным или отображением из М на N,если каждый элемент из N имеет, по крайней мере, один прообраз.

Определение. Отображение множества Мв множество Nназывается инъективным или взаимно однозначным, если каждый образ j(m) обладает ровно одним прообразом m.

Если отображение j(m) множества Мв множество Nинъективно и сюръективно, т. е. является взаимно однозначным отображением множества Мна множество N, то существует обратное отображение j^-1, которое каждому элементу n множества Nсопоставляет тот элемент из М, образом которого является n:

j^-1(n)= m, если j(m) = n.

Говорят, что множества Ми N равномощны или имеют одинаковую мощность, если существует взаимно однозначное отображение из Мна N.

Прямым произведением множеств МхК называют множество пар (m,k),где m ÎM, k ÎK.

1.56. Группы

Определение. Непустое множество G элементов произвольной природы (например, чисел, отображений) называется группой, если выполняются четыре следующих условия, которые называют аксиомами группы:

Аксиома1. Задан закон композиции, который каждой паре элементов а, b из G сопоставляет третий элемент этого же множества, называемый, как правило, произведением элементов а и b и обозначаемый через ab или через а × b. (Произведение может зависеть от порядка следования сомножителей: необязательно ab =bа.)

Аксиома 2. Закон ассоциативности. Для любых трех элементов а, b, с из G имеет место равенство

(a b) × с = а × (b с).

Аксиома3. В G существует (левая) единица е, т. е. элемент е, соследующим свойством:

е а = а " а Î G.

Аксиома4. Для " а Î G существует (по крайней мере) один (левый) обратный элемент а^-1 в G, определяемый свойством:

а^-1 а = е.

Аналогично определяются правая единица (ае=а) и правый обратный элемент (аа^-1=е). Если, кроме того, в группе выполняется закон коммутативности: ab = bа, то говорить о правых и левых элементах нет смысла. Группа, в которой выполняется закон коммутативности, называется абелевой.

Примеры. Если элементами рассматриваемого множества являются числа, а законом композиции служит обычное умножение, то для того, чтобы получить группу, прежде всего, следует исключить нуль, потому что у него нет обратного элемента; все рациональные числа, отличные от нуля, уже образуют группу (единичным элементом является число 1). Точно так же образуют группу числа -1 и 1, а также число 1 само по себе. Целые числа не образуют группу по умножению, так как обратные элементы не являются целыми.

В определение понятия группы тип операции (закона композиции) не входит. Хотя в аксиомах используется знак умножения: а × b, но операцией может служить и сложение.

Группа Gс операцией сложения в качестве закона композиции называется аддитивной группой.

В этом случае в аксиомах 1—4 следует всюду вместо «произведение а × b» читать «сумма a+b».

Роль единичного элемента е в аддитивной группе играет нулевой элемент 0 со свойством

0 + а = а " а Î G,

а роль обратного элемента а^-1 –элемент (- а)со свойством

- а + а = 0.

Обычно предполагают, что сложение – коммутативная oпeрация, т. е.

a + b= b + а.

Вместо a + (-b)пишут кратко а - b.

Примеры. Множество целых чисел образует аддитивную группу; четные числа тоже, а нечетные не образуют аддитивную группу так как сумма нечетных чисел дает четное число.

Число элементов конечной группы называется ее порядком.

Дальнейшие правила оперирования. Вводятся сложные произведения как произведения многих сомножителей и степени как призведения одинаковых сомножителей.

Возможность (двустороннего) деления:

5. Уравнение ах = b обладает решением в группеG, как и уравнение уа = b, где а и b — произвольные элементы изG.

А именно, этими решениями служат х = a^-1b и у = ba^-1.

6. Доказана однозначность деления: из ax=ay следует x=y.

1.57. Кольца и поля

Под системой с двойной композицией подразумевается произвольное множество элементов { а, b,..., },в котором для любых двух элементов a, b однозначно определены сумма a+b и произведение а × b, вновь принадлежащие данному множеству.

Система с двойной композицией (двумя операциями – сложением и умножением) называется кольцом, если операции над элементами этой системы подчиняются следующим законам:

I. Законы сложения:

а) Закон ассоциативности: a+(b+с) =(a+b) +с.

б) Закон коммутативности: a+b = b+a.

в) Разрешимость уравнения a+х=b для всех а, b.

II. Законы умножения:

а) Закон ассоциативности: a × bc = ab × с.

III. Законы дистрибутивности:

а) а × (b+с)= ab+ас;

б) (b + с)× а=bа + са.

Замечание1. Однозначная разрешимость в I.в не требуется, а получается дальше как следствие.

Замечание2. Если и для умножения выполняется закон коммутативности:

II. б): а × b=b × a,

то кольцо называется коммутативным.

Три закона I.а, I.б, I.в означают в совокупности, что элементы кольца образуют абелеву группу относительно сложения. Эту группу называют аддитивной группой кольца.

Кольцо называется телом, если:

а) в нем есть по крайней мере один элемент, отличный от нуля;

б) уравнения ах = b, и ya=b при а≠ 0 разрешимы.

Если тело коммутативно, то оно называется полем.

Отличные от нуля элементы тела составляют относительно операции умножения мультипликативную группу тела.

1.58. Классы вычетов

Пусть K — произвольное кольцо.

Чтобы некоторое подмножество в K вновь было кольцом (подкольцом кольца K), необходимо и достаточно, чтобы оно вместе с любыми а и b содержало разность (а – b) и произведение ab.

Среди подколец особую роль играют подкольца, называемые идеалами. Непустое подмножество M кольца K о называется идеалом, если:

1) из а Î M и b Î M Þ а-b Î M (свойство модулей);

2) из а Î M Þ аr Î M " r Î M.

Строго говоря, это определение правого идеала (модуль M вместе с каждым своим элементом а должен содержать все «правые кратные» аr). Аналогично определяется левый идеал. Наконец, подмножество M называется двусторонним идеалом, если оно является одновременно правым и левым идеалом, то есть умножение коммутативно.

Для коммутативных колец все три понятия совпадают, и поэтому говорят просто об идеалах.

Идеал M кольца K, являясь подгруппой аддитивной группы, определяет некоторое разбиение кольца K на смежные классы или классы вычетов по идеалу M.

Два элемента a, b называются сравнимыми по идеалу M или сравнимыми по модулю M, если они принадлежат одному классу вычетов, т. е. если а-b Î M.

Обозначение: а ≡ b mod M, или, а ≠ b mod M вместо «а не сравнимо с b».

1.59. Вычеты по модулю m

В криптографии используется алфавит, содержащий m символов алфавита в виде чисел. Он обозначается Z_m ={0,1,2.3,.... m -1}.

Определение: если для целых чисел a и b выполняется сравнение

а º b mod m,

то а называют вычетом b по модулю m и говорят: «а сравнимо с b по модулю m».

Операцию нахождения такого вычета называют приведением числа b по модулю m. Это означает, что для любого целого b (b > 0) его вычет a по модулю m есть некоторое целое число в интервале от 0 до (m -1), определяемое из соотношения

а = b + k × m, где k –целое число.

Фактически операция приведения целого числа по модулю m означает нахождение остатка от деления этого числа на m.

Например: 2 º 7 mod 5 или 64 º 1 mod 3.

Числа, сравнимые по модулю m, образуют класс вычетов по модулю m. Все числа из одного класса вычетов имеют один и тот же остаток от деления на на m, то есть любое число из этого класса является вычетом по модулю m. Таким образом, все бесконечное множество целых чисел разбивается на конечное число классов вычетов. Всего имеется m классов вычетов (по числу остатков от деления на m, каковыми могут быть числа от 0 до m -1). Множество Z_m целых чисел от 0 до (m -1) называют полным набором вычетов по модулю m.

Введем на множестве Z_m операции сложения и умножения целых чисел, которые выполняются по обычным правилам, но с приведением результата по модулю m. Целые числа с использованием операций сложения и умножения по модулю m образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности.

Таким образом, множество Z_m с определенными на нем операциями сложения и умножения с приведением результатов по модулю m является кольцом вычетов.

Обратный элемент по умножению а ^-1 определяется так, чтобы

а а ^-1º1 mod m.

Решение сравнения а · х º 1 mod m эквивалентно нахождению таких целых значений а и k, что

а х=m k+1.

Например, 37=21=1 mod 5 и 312=36=1 mod 5.

Из примера видно, что обратный элемент не является единственным, так что операция деления как умножения на обратный элемент определена в общем случае неоднозначно.

Обратный элемент существует не всегда.

Например, если модуль m = 26, то значения величин

2^-1 mod 26 и 13^-1 mod 26 не существуют.

Для существования и единственности обратного элемента необходимо, чтобы модуль m являлся простым числом. В этом случае существует обратная величина любого ненулевого элемента а Î Z_m, поскольку различаются все значения:

а mod m, 2а mod m, 3а mod m,.... (m- 1) а mod m, (1£ а £ m -1).

Множество Z_p, где р – простое число, является алгебраической системой, называемой конечным полем. Ненулевые элементы Z_p образуют мультипликативную группу.

Операция приведения по модулю m является гомоморфным отображением кольца вычетов на себя. То есть мы можем сначала приводить по модулю m, а затем выполнять операции либо наоборот, сначала выполнять операции, а затем приводить по модулю m. Это позволяет избежать громоздких вычислений с большими числами.

Определение. Приведенным набором вычетов Z_n ^* называют подмножество элементов полного набора вычетов (кольца) Z_n, взаимно простых с n.

Z_n ^* является алгебраической группой. Её также же называют мультипликативной группой конечного поля.

Эта группа содержит φ (n) элементов, где φ — функция Эйлера (см. ниже). Отметим, что если n – простое число, то приведенный набор вычетов Z_n ^* получается из полного набора вычетов Z_n удалением только одного элемента – нуля.

1.60. Функция Эйлера

Определение. Функцией Эйлера называется число положительных целых, меньших n и взаимно простых с n.

φ( n )= ½ Z_n^* ½.

Таблица значений функции Эйлера

n 2 3 4 5 6 7 8 9 10 11 12

φ (n) 1 2 2 3 2 6 4 6 4 10 4

Свойства функции Эйлера:

1) φ (1) = 1

2) φ (n^r) = n^r^-1 (n-1) " простого n и " натурального r.

Следствие: φ (n)= n- 1 " n – простого числа.

3) φ (a,b) = φ (а) φ (b) для любых натуральных взаимно простых а и b.

Свойство 3 вместе со следствием из свойства 2 позволяют легко вычислить значение функции Эйлера:

φ (n) = (p-1)(q-1),

если известно разложение числа n =pq на простые сомножители p и q.

В общем случае, если число сомножителей s в разложении n больше двух, используя каноническое разложение n на множители 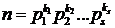, имеем

или

1.61. Поля Галуа

Многие криптосистемы базируются на полях Галуа. (Эварист Галуа - французский математик начала XIX века.). Вспомним, что поле есть множество, на котором определены операции сложения и умножения, удовлетворяющие требованиям: ассоциативности, коммутативности, дистрибутивности, существования аддитивного 0 и мультипликативной 1, аддитивных обратных и мультипликативных обратных для всех элементов за исключением 0.

Определение. Полем Галуа GF (p) называют кольцо вычетов Z_p, если р – простое:

GF ( p )= Z_p.

Определение. Мультипликативная группа Z_p ^* конечного поля GF (p) является циклической и содержит φ (р -1)образующих элементов, имеющих порядок р -1.

Определение. Некоторый элемент g Î Z_p ^* называют образующим, порождающим или примитивным элементом Z_p ^*, если для всех а Î Z_p ^* найдется такое целое х, что g^x=a mod p.

Определение. Если g^x=a mod p, то число х называют дискретным логарифмом элемента а по основанию g и модулю p.

Вычисление дискретных логарифмов (когда заданы g, а и p) примерно такая же труднорешаемая задача, как и разложение на множители.

Определение. Порядком элемента группы называется целое положительное число, равное числу различных элементов в циклической подгруппе, порождаемой этим элементом. (Если порядок элемента а равен p, то p является наименьшим из чисел, для которых a^p =1.)

Поскольку порядки всех элементов группы делят р -1, при р >2 элемент g примитивен тогда и только тогда, когда для любого простого делителя d числа p-1 значение g ⁽ ^p ^-1)/^d ¹ 1.

Если p - простое число, то любое число а Î[1,(p -1)] является взаимно простым с p, и поэтому обратный элемент p ^-1 имеет в поле Галуа единственное значение. Тем самым однозначно определяетcя операция деления.

Еще один тип поля Галуа, используемый в криптографии, основывается на арифметике по модулю неприводимых многочленов степени n, чьи коэффициенты — целые числа по модулю q, где q — простое. Эти поля Галуа обозначают как GF (qⁿ). Они имеют элементы, которые описываются многочленами степени не выше (n -1) в форме

а (х) = а_n_-1 xⁿ^-1+...+a₁x + а₀.

Каждый элемент а(x) является вычетом по модулю р(x), где р(x) - неприводимый многочлен степени n (т.е. р(x) нельзя разложить на сомножители - многочлены степени меньше n).

Арифметические действия над коэффициентами а выполняются по модулю q, а наивысшая степень x равна (n -1), так как выполняется приведение по модулю многочлена р (x), имеющего старшую степень n.

Если многочлен f нормирован (старший коэффициент равен 1), то он является минимальным многочленом над Z_p для любого своего корня а. Это означает, по определению, что если а — корень некоторого многочлена g Î Z_p [ x ], то f делит g.

Для целей криптографии обычно при построении GF (pⁿ) берется р =2, поскольку в этом случае элементы GF (2 ⁿ) представляются битовыми строками длины n и операции над ними легко реализуются на компьютере.

Мультипликативная группа поля GF (pⁿ) изоморфна группе корней из единицы степени рⁿ- 1, является циклической и содержит j(рⁿ -1) примитивных элементов поля. Если р =2 и рⁿ -1 — простое (так называемое простое число Мерсенна), то все элементы поля, кроме 0 и 1, примитивны.

Особый интерес представляют поля Галуа GF (2 ⁿ). Здесь коэффициенты а принимают значения 0 или 1. Поэтому многочлен а(x) степени не выше (n- 1) можно представить как вектор из n двоичных цифр:

a_n_-1 а_n_-2... a₁ a₀.

Каждый из n -битовых векторов соответствует конкретному элементу поля GF (2 ⁿ).

Например, поле Галуа GF (2³) имеет элементы:

Многочлены
0 1 х х +1 х ² х ²+1 х ²+ х х ²+ х +1