Таблицы значений синуса, косинуса, тангенса и котангенса составляются для углов от  до
до  (или от 0 до
(или от 0 до  ). Это объясняется тем, что их значения для остальных углов сводятся к значениям для острых углов.
). Это объясняется тем, что их значения для остальных углов сводятся к значениям для острых углов.
Задача. Вычислить  и
и  .
.
Заметим, что  . Следовательно, при повороте точки Р(1;0) вокруг начала координат на
. Следовательно, при повороте точки Р(1;0) вокруг начала координат на  точка совершит два полных оборота и ещё повернётся на угол
точка совершит два полных оборота и ещё повернётся на угол  , т.е. получится та же самая точка М, что и при повороте на
, т.е. получится та же самая точка М, что и при повороте на  (рис. 1). Поэтому
(рис. 1). Поэтому  .
.
Построим точку  , симметричную точке
, симметричную точке  относительно оси
относительно оси  (рис. 2). Ординаты точек
(рис. 2). Ординаты точек  и
и  одинаковы, а абсциссы различаются только знаком. Поэтому
одинаковы, а абсциссы различаются только знаком. Поэтому  .
.
Ответ:  .
.

Рис. 1 Рис. 2
При решении задачи 1 использовались равенства
 (1)
(1)
 (2)
(2)
Равенства (1) верны, так как при повороте точки Р(1;0) на угол 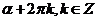 , получается та же самая точка, что и при повороте на угол
, получается та же самая точка, что и при повороте на угол  .
.
Следовательно, верны формулы
 (3)
(3)
Равенства (2) являются частными случаями формул

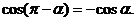 (4)
(4)
Докажем формулу 
Применяя формулу сложения для синуса, получаем  .
.
Аналогично доказывается и вторая из формул (4), которые называются формулами приведения. Вообще, формулами приведения для синуса называют следующие шесть формул:



 (5)
(5)


Следующие шесть формул называют формулами приведения для косинуса:



 (6)
(6)


Формулы (5) и (6) справедливы при любых значениях  .
.
Задача 2. Вычислить 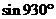 .
.
Используя первую из формул (3), получаем
 .
.
Если в формуле приведения угол  вычитается из числа
вычитается из числа  или прибавляется к этому числу, взятому нечётное число раз, то приводимая функция меняется на конфункцию; если же число
или прибавляется к этому числу, взятому нечётное число раз, то приводимая функция меняется на конфункцию; если же число  взято чётное число раз, то название приводимой функции сохраняется. Знак перед приведённой функцией ставится такой, каков знак приводимой функции в соответствующей четверти, если считать угол
взято чётное число раз, то название приводимой функции сохраняется. Знак перед приведённой функцией ставится такой, каков знак приводимой функции в соответствующей четверти, если считать угол  острым.
острым.
Результат этих вычислений представим в таблице
| Функция | 
| 
| 
| 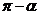
| 
| 
| 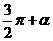
| 
|

| 
| 
| 
| 
| 
| 
| 
| 
|
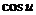
| 
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 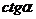
| 
| 
| 
|
Пример 3. Найти значение  .
.
Решение. Ясно, что 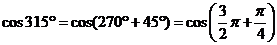 . По таблице находим (7-ой столбец, 2-я строка):
. По таблице находим (7-ой столбец, 2-я строка): 
Можно было бы  представить как
представить как  , и найти его значение по таблице на пересечении 8-го столбца и 2-ой строки.
, и найти его значение по таблице на пересечении 8-го столбца и 2-ой строки.
Пример 4. Привести к тригонометрической функции острого угла:
а)  ; б)
; б) 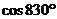 ; в)
; в)  .
.
Решение.
а)  ;
;
б)  ;
;
в) 
Формулы приведения запоминать необязательно. Для того чтобы записать любую из них, можно руководствоваться следующими правилами:
1) В правой части формулы ставится тот знак, который имеет левая часть при условии  .
.
2) Если в левой части формулы угол равен  или
или  , то синус заменяется на косинус, тангенс – на котангенс и наоборот. Если угол равен
, то синус заменяется на косинус, тангенс – на котангенс и наоборот. Если угол равен  , то замены не происходит.
, то замены не происходит.
Например, покажем, как с помощью этих правил можно получить формулу приведения для 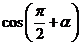 . По первому правилу в правой части формулы нужно поставить знак «-», так как если
. По первому правилу в правой части формулы нужно поставить знак «-», так как если  , то
, то  , а косинус во второй четверти отрицателен. По второму правилу косинус нужно заменить на синус, следовательно,
, а косинус во второй четверти отрицателен. По второму правилу косинус нужно заменить на синус, следовательно,  .
.
Итак, формулы (3), (7) и формулы приведения позволяют свести вычисление синуса, косинуса, тангенса и котангенса любого угла к вычислению их значений для острого угла.
Упражнения
1. Найти острый угол  , при котором выполняется равенство:
, при котором выполняется равенство:
1)  ; 2)
; 2) 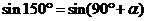 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 
2. Используя формулы приведения, вычислить:
1)  ; 2)
; 2) 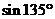 ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10) 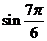 ; 11)
; 11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14) 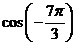 ; 15)
; 15)  ; 16)
; 16)  .
.
Упражнения
- Замените каждую из данных тригонометрических функций функцией
углов, меньших  :
:
а)  ; б)
; б) 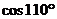 ; в)
; в)  .
.
2. Замените каждую из данных тригонометрических функций функцией углов, меньших  :
:
а)  ; б)
; б) 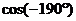 ; в)
; в)  .
.
3. Замените каждую из данных тригонометрических функций функцией углов, меньших  :
:
а)  ; б)
; б)  ; в)
; в)  .
.
4. Найдите:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 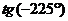 ; е)
; е)  .
.
5. Преобразуйте все тригонометрические функции каждого из следующих углов:
а) 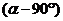 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Пример:

6. Найти область определения функции  . Является ли эта функция чётной?
. Является ли эта функция чётной?
7. Построить графики функций 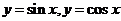 на отрезке
на отрезке  . Для каждой из этих функций найти значения
. Для каждой из этих функций найти значения  из данного отрезка, при которых
из данного отрезка, при которых  .
.
Таблица зависимостей углов поворота от длин отрезков:
| рад | 0 | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| град | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 |

| 0 | 
| 
| 
| 1 | 
| 
| 
| 0 | 
| 
| 
| -1 | 
| 
| 
|

| 1 | 
| 
| 
| 0 | 
| 
| 
| -1 | 
| 
| 
| 0 | 
| 
| 
|

| 0 | 
| 1 | 
| - | 
| -1 | 
| 0 | 
| 1 | 
| - | 
| -1 | 
|
| - | 
| 1 | 
| 0 | 
| -1 | 
| - | 
| 1 | 
| 0 | 
| -1 | 
|
Вопросы для самоконтроля:
- Что называется радианом?
- Как перевести градусную меру угла в радианную и, обратно, как перевести радианную меру угла в градусную?
- Как определяются тригонометрические функции числового аргумента?
- Какие знаки имеют тригонометрические функции в координатных четвертях?
- Какие тригонометрические функции являются чётными, а какие нечётными?
- Что называется периодом функции? Какие периоды имеют тригонометрические функции?
- Какими соотношениями связаны тригонометрические функции одного и того же аргумента?
- Сформулируйте теоремы для синуса суммы и разности двух углов.
- Сформулируйте теоремы для косинуса суммы и разности двух углов.
- Сформулируйте теоремы для тангенса суммы и разности двух углов.
- Сформулируйте теоремы для котангенса суммы и разности двух углов.
- Как выражаются тригонометрические функции двойных углов?
- Как выражаются тригонометрические функции половинных углов?
- По каким формулам преобразуются суммы и разности тригонометрических функций в произведения?
- По каким формулам преобразуются произведения тригонометрических функций в суммы и разности?
- Сформулируйте формулы приведения.
- Как построить графики тригонометрических функций?
- Перечислите обратные тригонометрические функции, области их определения и области значений.
- По каким формулам находятся решения простейших тригонометрических уравнений?
- Какие методы решения тригонометрических уравнений вы знаете?
 2018-03-09
2018-03-09 549
549








