2018-03-09
164
Используя полученные в эксперименте данные, определяют абсолютное давление, температуру и объем воздуха в цилиндре для каждого измерения.
Из уравнения состояния находят массу воздуха в цилиндре
, (2.1)
где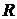 
– газовая постоянная воздуха, кДж/(кг·К);
, (2.2)
где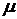 
– молярная масса воздуха, равная 28,96 кг/моль.
Удельный объем воздуха u, м3/кг, для каждого измерения определяется из соотношения
. (2.3)
Энтропия
, (2.4)
где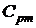 
– средняя массовая изобарная теплоемкость воздуха, кДж/(кг·К), определяется по формуле 
– определяется по температуре таблицы В.2;
– температура и давление при нормальных физических
условиях (
= 273 К; 
= 101,3 кПа).
Уравнение политропного процесса 
. Показатель политропного процесса n определяют по выражению
. (2.8)
Используя экспериментальные данные и найденный показатель политропы, проверяют справедливость соотношений
. (2.9)
Теплоту, участвующую в процессе, определяют по уравнению
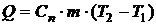, (2.10)
где 
– теплоемкость в политропном процессе:
, (2.11)
где 
– показатель адиабаты для воздуха, k =1,4.
Работу в процессе находят по уравнению
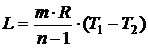. (2.12)
Изменение внутренней энергии определяется по формуле
. (2.13)
По результатам расчетов заполняют таблицу 2.2. Проверяют справедливость 1-го закона термодинамики для условий опыта.
. (2.14)
В р, u- и Т, s- координатах строят графики процессов.
Таблица 2.2 – Результаты расчетов
| № |  , кПа
|  , К
| V, м3 |  , м3/кг
|  , кДж/(кг×К)
|
Контрольные вопросы
1 Какие процессы называются политропными?
2 Назовите частные случаи политропных процессов.
3 Назовите приборы и способы определения основных характеристик состояния рабочего тела.
4 Изобразите графически частные случаи политропных процессов в р, u – и Т, s – координатах.
5 Как рассчитываются энергетические результаты процессов?
ЛАБОРАТОРНАЯ РАБОТА № 3
2 часа
Исследование термодинамического цикла
