Звеном второго порядка называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида
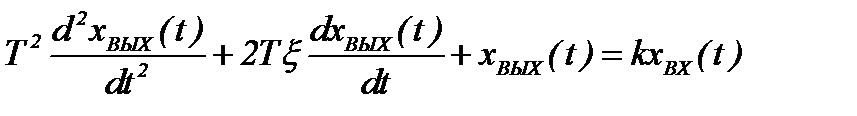 , (2.60)
, (2.60)
где Т – постоянная времени; ξ – относительный коэффициент затухания (демпфирования).
Применяя к (2.60) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
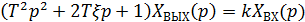 . (2.61) . (2.61)
|
В зависимости от вида корней характеристического уравнения инерционное звено второго порядка может иметь различные переходные характеристики. Это позволяет установить три разновидности звена – апериодическое, колебательное и консервативное.
При единичном входном воздействии для случая вещественных различных корней р1 и р2 по уравнению (2.61) получим переходную функцию (ξ≥1):
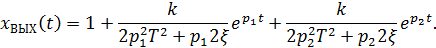
В случае вещественных корней апериодическое звено второго порядка эквивалентно последовательному соединению двух инерционных звеньев первого порядка, поэтому передаточная функция может быть записана в виде
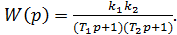
По выражению W(p) после замены р на jω получим частотную функцию W(jω) апериодического звена второго порядка, которая определяет частотные характеристики звена.
Колебательное звено
Если корни уравнения (2.61) будут комплексными, то инерционное звено второго порядка станет колебательным (ξ< 1).
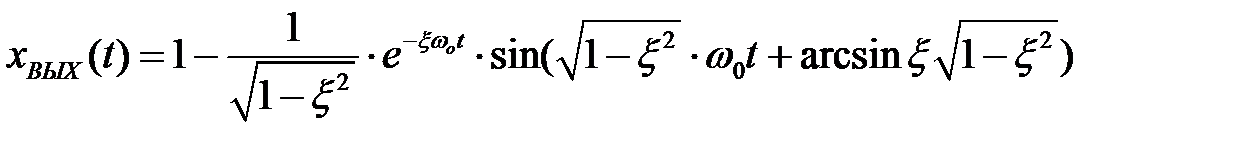 , (2.62)
, (2.62)
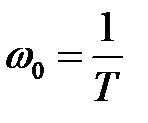 где .
где .
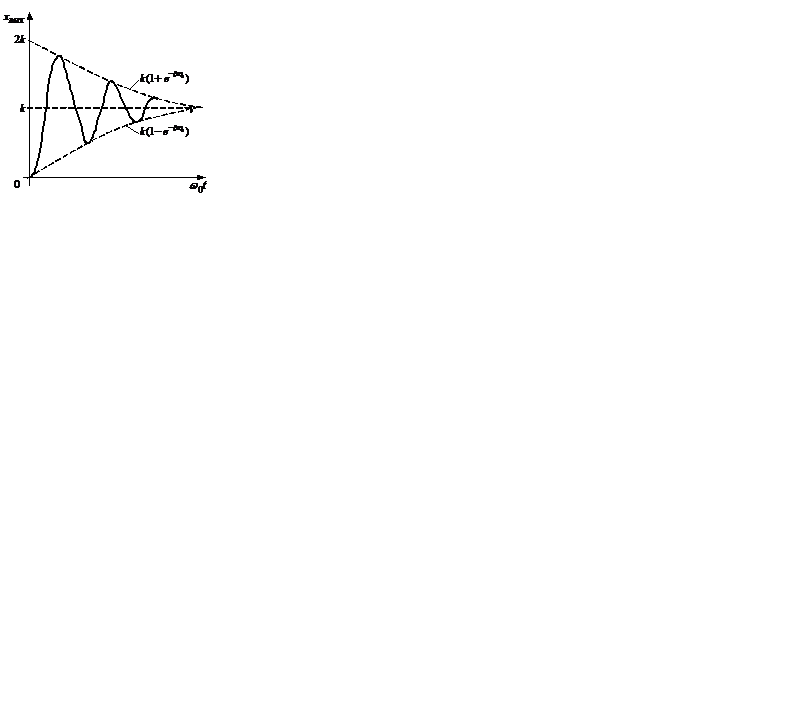 График переходной функции колебательного звена показан на рисунке 2.19. Примерами колебательного звена могут служить упругая механическая система с существенным влиянием массы, электрический колебательный контур и т.д.
График переходной функции колебательного звена показан на рисунке 2.19. Примерами колебательного звена могут служить упругая механическая система с существенным влиянием массы, электрический колебательный контур и т.д.
По уравнениям (2.61) определяется передаточная функция инерционного звена
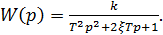 (2.63)
(2.63)
На основании W(p) получим выражение для амплитудно-фазовой характеристики W(jω)
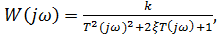 (2.64)
(2.64)
Рисунок 2.19
по которой при различных значениях коэффициента затухания можно построить серию частотных характеристик колебательного звена (рисунок 2.20). Как видно из рисунка, годограф частотной характеристики проходит через два квадранта – IY и III – пересекает мнимую ось при ωТ=1, когда в выражении (2.63) 1+ (jωT)2 =0. При этом 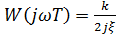 .
.
С уменьшением ξ петля, очерченная годографом, увеличивается, и при ξ =0 характеристика вырождается в две полупрямые: 1 – от W(j ωT)=k до W(j ωT)→∞ при 0 < ωT<1 до 2 – от W(j ωT)→-∞ до W(j ωT)=0 при 1 < ωT<∞.
Амплитудно-частотная и фазо-частотная характеристики колебательного звена выражаются уравнениям
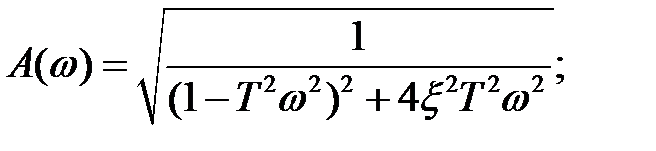 (2.65)
(2.65)
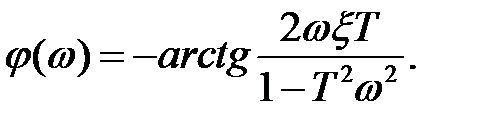 (2.66)
(2.66)
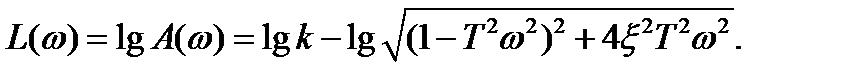 Логарифмическая амплитудно-фазовая характеристика колебательного звена описывается уравнением
Логарифмическая амплитудно-фазовая характеристика колебательного звена описывается уравнением
(2.67)
Вблизи точки резонанса (ωT=1) эта характеристика сильно зависит от коэффициента затухания ξ. С удалением от резонансной частоты характеристика практически перестаёт зависеть от ξ.
Для колебательных звеньев пользуются асимптотическими характеристиками
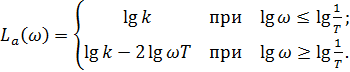 (2.68)
(2.68)
Поправка к асимптотической характеристике
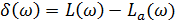
зависит от коэффициента затухания ξ. Графики L(ω) и φ(ω) для различных ξ показаны на рисунке 2.21. У колебательных звеньев возникает всплеск при 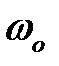 .
.
Рисунок 2.21
Консервативное звено
Уравнение динамики консервативного вена имеет вид
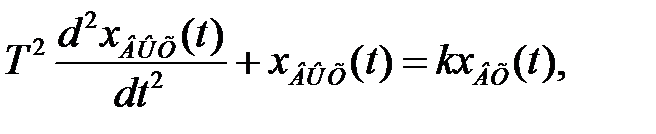 (2.69)
(2.69)
где Т – постоянная времени;
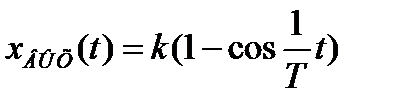 k – коэффициент усиления (или передачи).
k – коэффициент усиления (или передачи).
Переходный процесс такого звена показан на рисунке 2.22.
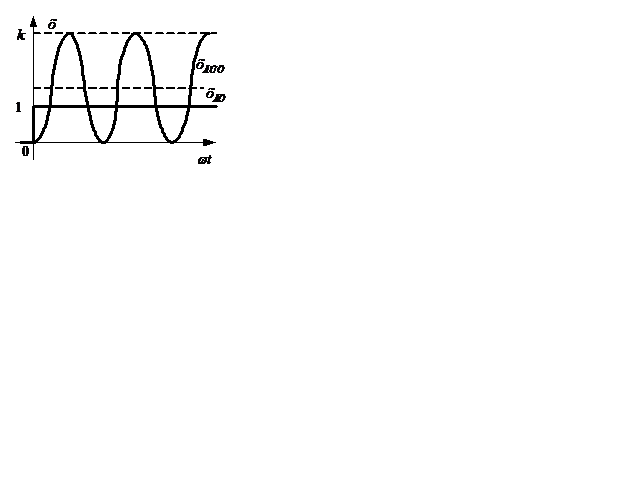
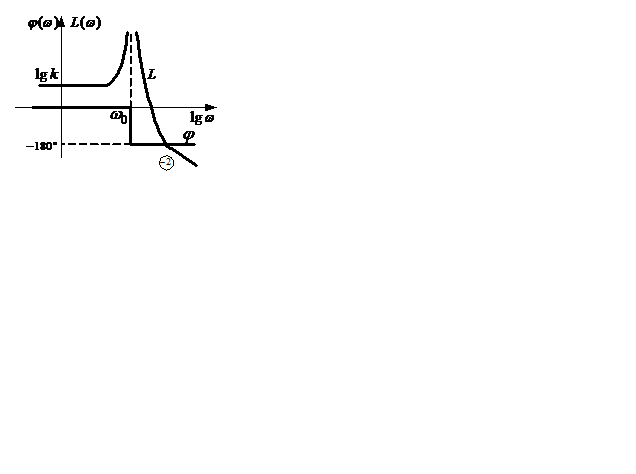
Рисунок 2.22
Рисунок 2.23
Консервативное звено – частный случай звена второго порядка, когда отсутствует демпфирование (ξ=0). Применяя к (2.69) преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение
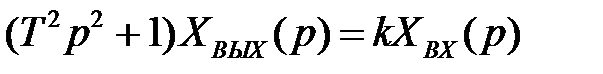 .
.
Передаточная функция консервативного звена
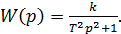 (2.70)
На основании (2.70) получим частотную функцию (2.70)
На основании (2.70) получим частотную функцию
|
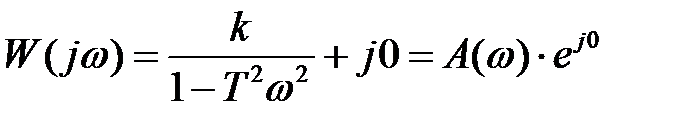 , (2.71)
, (2.71)
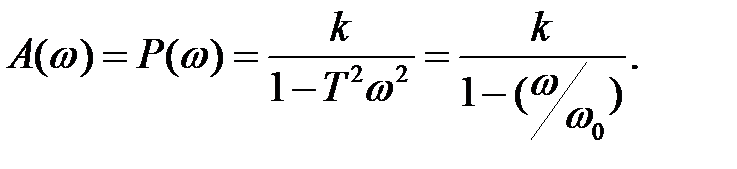 где
где
(2.72)
Логарифмическая амплитудно-частотная характеристика имеет разрыв при ω=ω0 (рисунок 2.23), что свидетельствует о возникновении незатухающих колебаний с этой частотой. Логарифмическая амплитудно-частотная характеристика может быть представлена в виде двух отрезков прямых линий. Одна линия уходит при lgω0≤lgω<∞ вправо от точки lg ω0 под углом -2 лог/дек; вторая линия при -∞<lgω≤ lgω 0 совпадает с линией lg k праллельной оси абсцисс.
Фазо-частотная характеристика определяет скачкообразное изменение фазы при ω=ω0 от нуля до -180° (рисунок 2.23). Звено является минимально-фазовым.
Примером консервативного звена может служит идеальный пассивный четырёхполюсник, состоящий из L и С (при отсутствии омического сопротивле- ния цепи), и другие элементы, если уравнения их динамики имеют вид уравнения (2.69).
 2018-03-09
2018-03-09 1526
1526
