2018-03-09
148
Рассмотрим не матричную, а формальную запись МПИ: 
Итак, получаем следующие формулы для МПИ:
(2.7)
В методе Зейделя в отличие от МПИ при вычислении координат вектора 
будем использовать не только лишь координаты вектора 
с предыдущего шага, но и уже найденные координаты вектора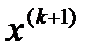 
.
(2.8)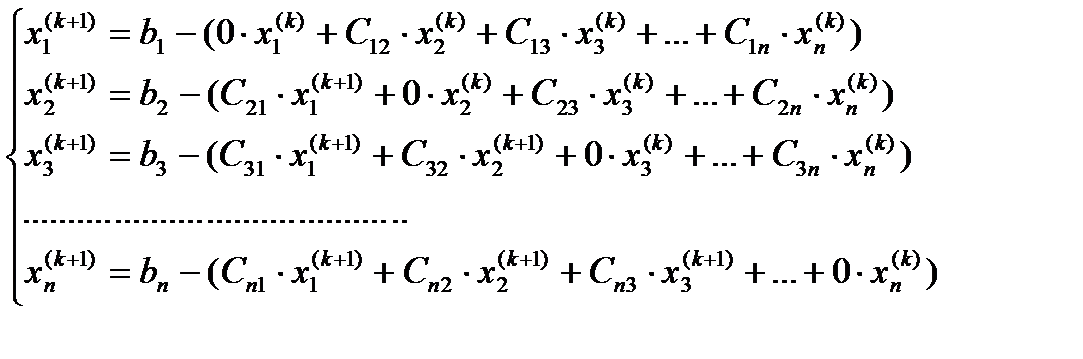 
Метод Зейделя сходится при условии 
(как и МПИ). Сходится немного быстрее, но в целом скорость сходимости, как и в МПИ, не хуже геометрической прогрессии со знаменателем 
.
Можно также использовать формулу из следствия 2.7.
Оценка трудоемкости решения СЛАУ различными методами:
Сравним метод Гаусса и МПИ:
Гаусс - 
МПИ - 
, где n – размер матрицы, N – количество итераций.
Если N велико, а n – мало, то метод Гаусса выгоднее.
Если же N – не очень большое, а n – велико (размер матрицы большой, но сходится довольно быстро), тогда выгоднее итерационный метод.
Замечание:
на практике метод Гаусса очень плохо работает с матрицами больших размеров, а итерационные методы одинаково успешно справляются с матрицами любых размеров. С другой стороны метод Гаусса работает всегда, а МПИ работает при условии 
, т.е. применим не для всех СЛАУ.
Вывод: для решения некоторых СЛАУ выгоднее использовать точные методы (метод Гаусса), а для некоторых – приближенные.
Тема 3. Методы решения нелинейных уравнений (НУ) и систем нелинейных уравнений (СНУ).
П.1 НУ и СНУ.
Будем рассматривать только системы, где количество уравнений совпадает с количеством неизвестных (как и в СЛАУ).
