Метод конечных разностей

ЗАЧЕТНАЯ РАБОТА

 

По курсу «Математическое моделирование в

строительстве»

 

Выполнила студентка гр. СТ-25

Максименко Д.А.

 

Принял преподаватель

Буравлев В.Ф.

 

Киров 2014

Вариант 15-В

 

q(x)= q₀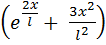

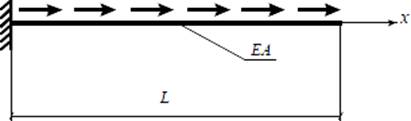
Рис. 1. Расчетная схема

Точное решение

Дифференциальное уравнение равновесия имеет вид:

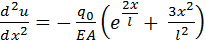_.                                   (1.1)

Дважды интегрируем

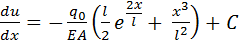₁;              

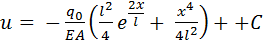₁x+ C_2.                      (1.2)

Удовлетворяем геометрическому граничному условию на левом торце

u(0) =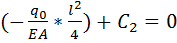

откуда

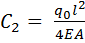(1.3)

Удовлетворяем статические граничные условия на правом торце

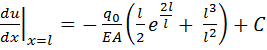₁ = 0,

откуда

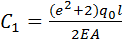.(1.4)

 

 Внося полученные константы интегрирования (1.3) и (1.4) во второе

соотношение (1.2), приходим к выражению для продольного перемещения

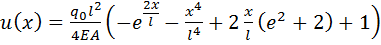(1.5)

Умножая на EА и беря производную по x, получим выражение для

нормального усилия

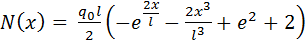(1.6)

 

Произведем расчет перемещений и усилий по формулам (1.5) и (1.6) c

помощью программы на языке программирования «Pascal» в пяти

равноотстоящих точках и сведем результаты расчета в таблицу 1.

PROGRAM STTP;

usescrt;

Const

g=1.0; EA=1.0; l=1.0; m=4;

Var

i:integer;

dx,x,x2,nn,uu: real;

u,n: array[1..m+1] of real;

Begin

clrscr;

writeln;

writeln ('Результатырасчета');

writeln;

writeln ('Координаты перемещения усиления');

dx:=l/m;

nn:=g*l/2;

uu:=nn*l/(4*EA);

fori:=1 to m+1

do begin;

x:=dx*(i-1)/l;

x2:=sqr(x);

U[i]:= {uu*} (-exp(2*x)-x*x*x*x+2*x*(exp(2)+2)+1);

N[i]:= {nn*} ((-exp(2*x)-2*x*x*x+exp(2)+2));

writeln;

writeln ('x=', x:4:2, ' U= ', u[i]:6:3, ' N=', N[i]:6:3);

readln;

End.

Представим результаты расчета в виде таблицы 1 и графиков (рис. 2 и 3)

Таблица 1

х	0	0,25	0,5	0,75	1
	0	4.042	7.608	10.285	11.389
	8.389	7.709	6.421	4.064	0

 

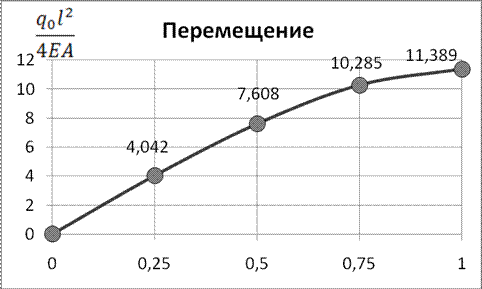
Рис. 2. Изменение перемещения по длине стержня (точное решение)

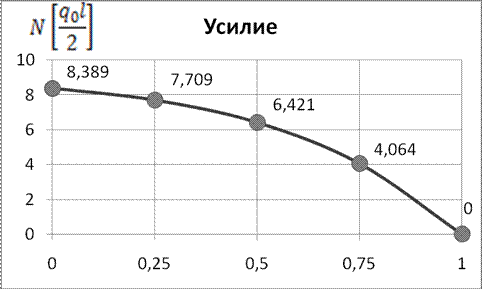
Рис. 3. Изменение продольного усилия по длине стержня (точное решение)

Приближенные решения

Метод конечных разностей

 

Обозначим узловые точки (1-5) в местах разбиения стержня на четыре

элемента и введем законтурную точку 6 (рис. 4).

q(x)= q₀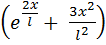

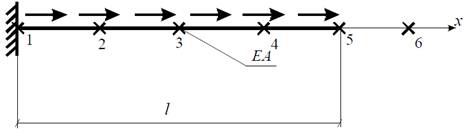
Рис. 4. Разбиение стержня на элементы

       Запишем дифференциальное уравнение в конечно-разностной форме

u_i-1 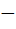 2u_i+ u_i+1= 𝛼 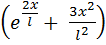_. (2.1.1)

Здесь введено обозначение

𝛼 = 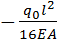. (2.1.2)

      Запишем уравнение для всех внутренних точек, причем для крайней

правой точки 5 запишем статическое граничное условие через законтурную

точку 6:

i = 2; u₁ – 2u₂ + u₃  = 1,8361𝛼;

i = 3; u₂ – 2u₃ + u₄  = 3.468 𝛼;

i = 4; u₃ – 2u₄ + u₅  =6.1685 𝛼;       (2.1.3)

i = 5; u₄ – 2u₅ + u₆  = 5.1938𝛼;

.

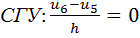Выполним прямой ход, учитывая левое геометрическое граничное

условие (u ₁= 0):

u₆ =u₅;

u₄ – 2u₅ + u₅ = 5.1938𝛼⟹ u₅=u₄ – 5.1938𝛼;    

u₃ – 2u₄ + u₄ – 5.1938𝛼 = 6.1685 𝛼⟹ u₄=u₃ – 11.3623𝛼;  (2.1.4)

u₂ – 2u₃ + u₃ – 11.3623𝛼 = 3.468 𝛼⟹ u₃=u₂ –14.8303 𝛼;

u₁ – 2u₂ + u₂ – 14.8303𝛼 = 1.8361𝛼⟹ u₂= – 16.6664𝛼.

Выполним обратный ход, раскрывая 𝛼 и приводя результат к размерности

точного решения:(2.1.5)

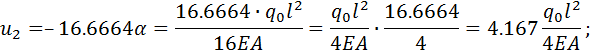
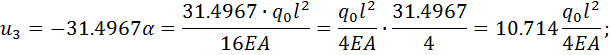
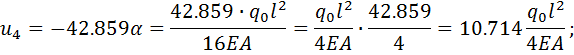
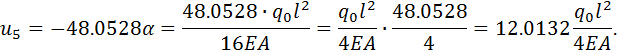
      Осуществим переход к нормальным усилиям с учетом размерностей

для перемещений и усилий в точном решении при помощи соотношения

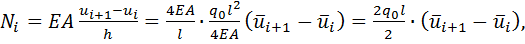(2.1.6)

где черта над u обозначает, что берутся только ее численные значения.

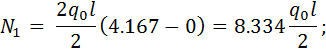
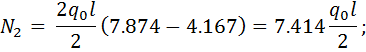
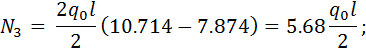
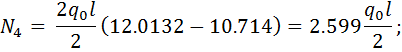
 (2.1.7)

       Воспользуемся соотношением, осуществляющим переход к усилиям с

помощью дифференцирующей матрицы

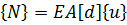,          (2.1.8)

которое в раскрытом виде с учетом числа элементов (h=l/4) и размерностей,

использованных для перемещений и усилий в точном решении, запишется

так:

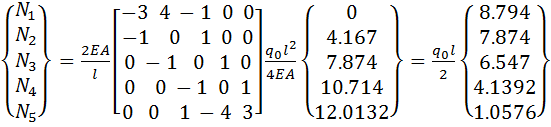(2.1.9)

Результаты расчета представим в виде таблицы 2 и графиков (рис. 5,6).

Таблица 2

x	0	0,25	0,5	0,75	1,0
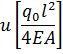
	0 (0)	4.167 (4.042)	7.874 (7.608)	10.714 (10.285)	12.0132 (11.389)
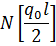
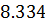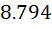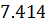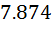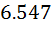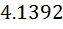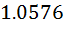	* ** (8.389)	* ** (7.709)	5.68* ** (6.421)	2.599* ** (4.064)	-* ** (0)

 

 

(…) – точное решение; *- решение в рамках МКР; **- решение с помощью

дифференцирующей матрицы.

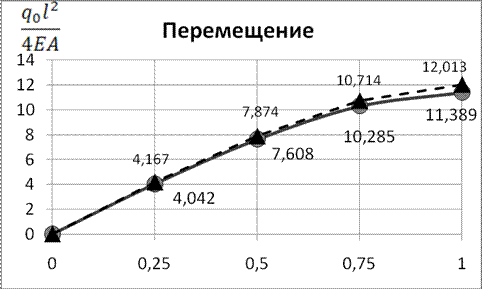
Рис. 5. Изменение перемещения по длине стержня (метод конечных

разностей)

 

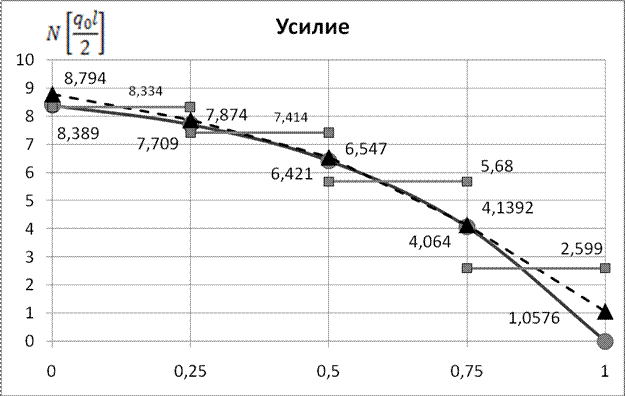
Рис. 6. Изменение продольного усилия по длине стержня (метод конечных

разностей)