Первая теорема Вейерштрасса.
Если f(x) непрерывна на [a,b], то она ограничена на этом отрезке. 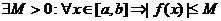 .
.
Вторая теорема Вейерштрасса.
Если f(x) непрерывна на [a,b], то она достигает на этом отрезке своего наименьшего (наибольшего) значения.
Первая теорема Больцано-Коши.
Функция 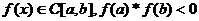 , тогда
, тогда 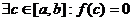
Доказательство: [a,b] разделим пополам и получим отрезки [a,a+b/2] и [a+b/2,b]. Из них выберем тот, на концах которого ф-ция принимает значения, разные по знаку и обозначим [a1,b1], f(a1)*f(b1)<0. С этим отрезком поступим так же. [a1,a1+b1/2] и [a1+b1/2,b1]. Выберем отрезок с разными по знаку концами. Когда-нибудь получим отрезок 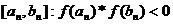 .
. 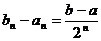 . При
. При 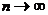 ,
, 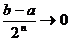 . Получим систему вложенных отрезков
. Получим систему вложенных отрезков 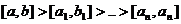 . Если при делении отрезка пополам значение функции в середине отрезка равно нулю, то теорему можно считать доказанной. Система вложенных отрезков, длина которых стремится к нулю, имеет одну общую точку => существует точка С. Докажем, что f(с)=0. Предположим, что
. Если при делении отрезка пополам значение функции в середине отрезка равно нулю, то теорему можно считать доказанной. Система вложенных отрезков, длина которых стремится к нулю, имеет одну общую точку => существует точка С. Докажем, что f(с)=0. Предположим, что 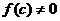 . Для определенности f(c)>0. Т.к. ф-ция непрерывна на отрезке [a,b], то она непрерывна в точке С. Раз f(c)>0, то
. Для определенности f(c)>0. Т.к. ф-ция непрерывна на отрезке [a,b], то она непрерывна в точке С. Раз f(c)>0, то 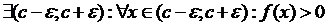 ;
; 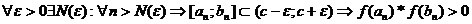 - притиворечие, что и треб. доказ.
- притиворечие, что и треб. доказ.
Вторая теорема Больцано-Коши.
Пусть  непрерывна на [a,b] и на концах отрезка принимает значения B и A, (
непрерывна на [a,b] и на концах отрезка принимает значения B и A, ( , тогда для любого числа С:
, тогда для любого числа С:  .
.
Доказательство. Рассмотрим F(x)=f(x)-C.
1) F(x) непрерывна на отрезке, как разность двух непрерывных функций.
2) F(a)*F(b)<0
По первой теореме Б-К  .
.
Билет №22.
Доказать первое достаточное условие экстремума функции.
Пусть функция  определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку х из указанной окрестности, тогда на  :
:
3.  - непрерывна.
- непрерывна.
4. на  - дифференцируема.
- дифференцируема.
По т. Лагранжа  , где
, где  , т.к.
, т.к.  , то
, то 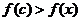
на  :
: 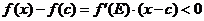 где
где  ,
, 
Вывести 1 замечательный предел: 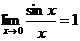
 Пусть
Пусть  ,
,  .
.
Ясно, что  , но
, но


 , т.е.
, т.е.
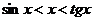 , т.к.
, т.к.  .
.
Билет №23.
Доказать второе достаточное условие экстремума.
Пусть функция  определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ая производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если
определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ая производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если  , то x=c – локальный минимум, если
, то x=c – локальный минимум, если  , то x=c – локальный максимум.
, то x=c – локальный максимум.
Доказательство: Запишем формулу Тейлора с остаточным членом в форме Пеано с центром в точке С.
 , где
, где  - б.м.ф. при
- б.м.ф. при  . Пусть n – четное, тогда
. Пусть n – четное, тогда 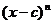 не меняет знак при переходе через С.
не меняет знак при переходе через С. 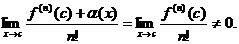
 в которой функция сохраняет знак своего предела.
в которой функция сохраняет знак своего предела.  ,
,  .
. 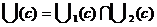 .
.  , если
, если  - точка локального экстремума.
- точка локального экстремума.
Вывести уравнение касательной и нормали к плоской кривой.
С геометрической точки зрения значении производной  в данной точке x=a равно угловому коэффициенту касательной к графику ф-ции
в данной точке x=a равно угловому коэффициенту касательной к графику ф-ции  в точке М(a,f(a)). Из аналит. геометрии известно, что уравнение прямой с заданным угловым коэффициентом k и проходящей через точку M(a,f(a)) имеет вид:
в точке М(a,f(a)). Из аналит. геометрии известно, что уравнение прямой с заданным угловым коэффициентом k и проходящей через точку M(a,f(a)) имеет вид:  .
.
Прямую, проходящую через точку М, перпендикулярно касательной называют нормалью к графику функции в точке М. Если  , то уравнение нормали имеет вид:
, то уравнение нормали имеет вид: 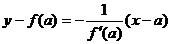 .
.
Предельное положение секущей при  называют касательной к графику функции в точке М.
называют касательной к графику функции в точке М.  .
. 
Билет №24.
Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
Теорема. Пусть ф-ции f(x) и g(x) определены и дифференцируемы в  , представляют собой б.м.ф. при
, представляют собой б.м.ф. при  , причем
, причем  в
в  . Если
. Если  .
.
Доказательство: Рассмотрим {  . Доопределим по непрерывности данные функции нулем в точке a (f(a)=0, g(a)=0). Тогда на [a,
. Доопределим по непрерывности данные функции нулем в точке a (f(a)=0, g(a)=0). Тогда на [a, 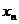 ] функции f(x) и g(x) непрерывны, на (a;
] функции f(x) и g(x) непрерывны, на (a; 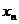 ) f(x) и g(x) дифференцируемы. По теореме Коши
) f(x) и g(x) дифференцируемы. По теореме Коши 
 при
при 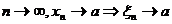 по условию теоремы
по условию теоремы  >
>
Замечание 1: точка а может быть бесконечной, тогда 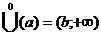 или
или  Формулировка: пусть f(x) b g(x) определены и дифференцируемы на
Формулировка: пусть f(x) b g(x) определены и дифференцируемы на  и представл. б.м.ф. при
и представл. б.м.ф. при  , причем
, причем  Если
Если 
Замечание 2: если  и
и  удовлетворяют всем условиям Б-Л и
удовлетворяют всем условиям Б-Л и  , то
, то  и т. д.
и т. д.
Вывести формулу для производной частного от деления двух функций.
Пусть функции u(x) и v(x) дифференцируемы в точке, тогда дифференцируемыми в этой точке будут u(x)/v(x), причем 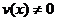 ,
,  .
.
Док-во:

Билет №25.
Доказать первое достаточное условие экстремума функции.
Пусть функция  определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку х из указанной окрестности, тогда на  :
:
5.  - непрерывна.
- непрерывна.
6. на  - дифференцируема.
- дифференцируема.
По т. Лагранжа  , где
, где  , т.к.
, т.к.  , то
, то 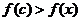
на  :
: 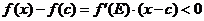 где
где  ,
, 
Сформулировать определение функции, непрерывной на отрезке. Свойства функций, непрерывных на отрезке.
Функцию f(x) называют непрерывной на [a,b], если она непрерывна на (a,b) и непрерывна справа в точке x=a и непрерывна слева в точке x=b.
 2018-02-13
2018-02-13 2791
2791