2018-02-13
227
Пусть 
непрерывна на [a,b] и на концах отрезка принимает значения B и A, (
, тогда для любого числа С: 
.
Доказательство. Рассмотрим F(x)=f(x)-C.
3) F(x) непрерывна на отрезке, как разность двух непрерывных функций.
4) F(a)*F(b)<0
По первой теореме Б-К 
.
Билет №26.
Доказать теоремы Ролля и Ферма.
Пусть дана функция 
.
1. Определена и непрерывна на отрезке 
.
2. Дифференцируема на интервале 
.
3. И на концах отрезка принимает одинаковые значения.
Тогда существует точка 
, принадлежащая отрезку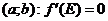 
.
Доказательство: Т.к. функция непрерывна на отрезке , то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
, 
,
, .
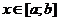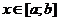Случаи:
1. 
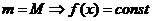, - любое из интервала
2. 
в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке отрезка .
Согласно второму условию теоремы Ролля, функция дифференцируема на интервале в любой точке, то по теореме Ферма существует 
.
Т. Ферма:
Пусть y=f(x) определена на (a;b) и в некоторой точке этого интервала принимает наибольшее или наименьшее значение. Если в этой точке функция имеет производную, то эта производная равна нулю.
|
|
|
Доказательство: (Для наибольшего значения). Пусть 
. 
; 
; Т.к. 
.
Вывести формулу для производной обратной функции.
Пусть функция y=f(x) строго монотонна (возрастает или убывает) в некоторой окрестности точки 
, и дифференцируема в точке , тогда 
- дифференцируемая в точке 
.
Доказательство: Рассмотрим 
, пусть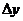 
- приращение аргумента обратной функции в точке 
, тогда функция получит приращение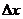 
, 
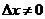в силу строгой монотонности функции.
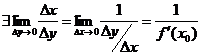
Билет №27.
Необходимое и достаточное условие существования точки перегиба графика функции. Доказать достаточное условие.
