1. Разложите на множители  , если а= 3, b=14, с=-5
, если а= 3, b=14, с=-5
Рассмотрим уравнение 3х2+14х-5=0
D=b2-4ac=142-4·3·(-5)=196+60=256=162
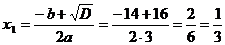

Тогда 3х2+14х-5=3(х-1/3)(х+5)=(3х-1)(х+5)
Ответ: 3х2+14х-5=(3х-1)(х+5)
2. Постройте графики функций
а)  ; б)
; б)  ; в)
; в)  , если а= 2, b= -3, c=1
, если а= 2, b= -3, c=1
а) Рассмотрим функцию у=2х-3. График этой функции – есть прямая. Для построения прямой достаточно знать координаты двух точек на ней:
| х | 0 | 2 |
| у | -3 | 1 |
б) Рассмотрим функцию у= 2х2+1. График функции – парабола, ветви направлены вверх. Для её построения необходимо знать координаты как минимум 5 точек:
| х | 0 | 1 | -1 | 2 | -2 |
| у | 1 | 3 | 3 | 9 | 9 |
в) Рассмотрим функцию у=2х3. Это возрастающая функция (т.к. х1=-2, х2=3, х1<х2, то у1=2·(-2)3=-16 < у2=2·(3)3=54. График – кривая. Для её построения необходимо знать координаты как минимум 5 точек:
| х | 0 | 1 | -1 | 2 | -2 |
| у | 0 | 2 | -2 | 16 | -16 |


 у
у
| 9 | б) | ||||||||

| 7 | ||||||||
| 5 | а) | ||||||||
| 3 | |||||||||
| 1 | |||||||||
 -3 -3
| -2 | -1 | 0 | 1 | 3 | 5 | х | ||
| -1 | |||||||||
| -3 | |||||||||
| в) |
3. Вычислить пределы
3.1.  3.2
3.2  3.3.
3.3.  3.4.
3.4.  3.5.
3.5. 
Число А называется пределом функции y = f(x) при  , если для любого числа
, если для любого числа 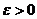 , существует
, существует  такое, что при
такое, что при  выполняется неравенство
выполняется неравенство  .
.
3.1. 
Функция  – непрерывная, графиком ее является парабола. Следовательно, заменяя ее аргумент предельным значением, найдем значение предела:
– непрерывная, графиком ее является парабола. Следовательно, заменяя ее аргумент предельным значением, найдем значение предела:
 .
.
Ответ: –8.
3.2. 
При непосредственном нахождении предела и числитель и знаменатель обращаются в нуль, таким образом, получается неопределенность вида  .
.
Чтобы раскрыть неопределенность  , разложим числитель на множители:
, разложим числитель на множители:
 ,
,
Тогда 
Ответ: 7.
3.3. 
При  непосредственно подстановкой имеем неопределенность вида
непосредственно подстановкой имеем неопределенность вида  .
.
Чтобы раскрыть неопределенность, разделим числитель и знаменатель дроби на наивысшую степень переменной –  . Тогда
. Тогда

Поскольку  , то
, то  .
.
Ответ: 2.
3.4. 
Найдем предел, используя первый замечательный предел 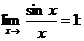


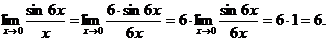
Таким образом:  .
.
Замечание:
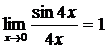 , так как если
, так как если  , то
, то 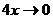 . Значит
. Значит  .
.
Ответ: 
3.5. 
Преобразуем выражение, стоящее под знаком предела, к виду  ,
,
и используем второй замечательный предел 

Если  , то
, то 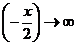 . Значит:
. Значит:


Ответ: 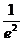 .
.
4. Для данной функции: найти точки разрыва, скачок функции в каждой точке разрыва, сделать чертеж

Функция является непрерывной на множестве, если она непрерывна в каждой точке множества.
Функция непрерывна в точке тогда и только тогда, когда малому приращению аргумента соответствует малое приращение функции.
Функция является непрерывной в точке, если  .
.
Точки, в которых нарушается условие непрерывности называются точками разрыва.
Если односторонние пределы в точке конечны, то она является точкой разрыва 1 рода. Если односторонние пределы в точке равны, то она является точкой устранимого разрыва.
Точками подозрительными на разрыв являются х=-2, х=2.
х=-2
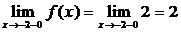

Оба односторонних предела – конечны, не равны. Значит, х=2 – точка разрыва 1 рода. Скачок функции Δ= |2-0|=2.
х=2


Так как один из односторонних пределов бесконечен, значит х=2– точка разрыва 2 рода.
| 9 | ||||||||
| 7 | |||||||||
| 5 | 
| ||||||||
| 3 | |||||||||

| 
| ||||||||
| 1 | |||||||||
 -3 -3
| -2 | -1 | 0 | 1 | 3 | 5 | х | ||
| -1 | |||||||||
| -3 | |||||||||
Ответ: функция не является непрерывной на всём множестве.
5. Определить значение равновесной цены спроса и предложения, если заданы функция спроса и предложения, где р– цена товара. Сделать чертеж.
 Функция предложения
Функция предложения  , функция спроса
, функция спроса 
Равновесная цена спроса и предложения есть такое значение цены, при котором функции s и q принимают равные значения. Искомая точка есть точка пересечения двух прямых s и q.
Каждая функция определяется графиком в виде прямой
| р | 1 | 3 |
| s | 4 | 10/3 |
| p | 0 | 2 |
| q | 2 | 5 |


 s,q s,q
|  9 9
| ||||||||
| 7 | |||||||||
 5 5
| |||||||||
| 3 | |||||||||
| 1 | |||||||||
 -3 -3
| -2 | -1 | 0 | 1 | 3 | 5 | р | ||
| -1 | |||||||||
| -3 | |||||||||
Пересечение в точке р=1,2.
Определим погрешность вычисления. Найдем точку пересечения линий как общую точку линий.
 ,
,  ,
, 


Погрешность |1.2-1.2|=0.
Ответ: равновесная цена спроса и предложения равна 1,2.
 2018-02-13
2018-02-13 168
168







