Тема: Задачі розпізнавання на графах.
Мета: Навчитися формулювати твердження для розпізнавання геометричних фігур.
Вступ. Дискретні моделі дозволяють спростити розуміння явищ реального світу. Застосування будь-якої дискретної моделі залежить від того, чи змогли ви розпізнати цю модель в конкретних досліджуваних даних, чи ні. Отже, успіх застосування математики банально залежить від процесів розпізнавання вашим мозком математичних закономірностей, які є у реально існуючих явищах. Розпізнавання відбувається як процес порівняння певних ознак, які мозок виділяє при спостереженні реального явища з ознаками, які присутні в абстрактній моделі. Якщо для певної моделі кількість ознак перевищує бар’єр, то включається механізм логіки, який знайде найкраще відображення ознак реального явища в ознаки математичної моделі. Процес розпізнавання – це також модель. Почнемо з розпізнавання елементарних геометричних фігур на площині.
Розпізнавання об’єктів пов’язано з визначенням геометричних властивостей ліній, якими вони відображаються на площині. Якщо для деякої лінії на малюнку існує інтерпретація такої ж лінії, що належить об’єктові, то приймається гіпотеза, що на малюнку є заданий об’єкт. Цю гіпотезу можна підтвердити, або спростувати, якщо порівняти співвідношення між лініями на малюнку з відповідними лініями на об’єкті, який розпізнається. Для прикладу розглянемо наступний малюнок (Рис.2).
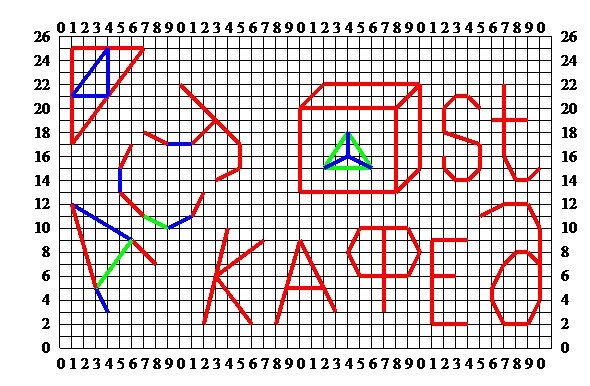
Рис. 2. Представлення букв окремими відрізками на площині.
Нехай на площині існують деякі відрізки (Рис.2) та існує абстрактний опис того, як повинна виглядати та чи інша буква алфавіту. Наприклад, букву «А» можна описати як дві лінії, приблизно однакового розміру, які утворюють гострий кут, і ці лінії перехрещуються третьою лінією, яка приблизно паралельна уявній лінії, на якій розташовані кінці перших двох ліній. Необхідно розпізнати, які з ліній на площині підходять під заданий опис.
Опис об’єктів зручно здійснювати за допомогою тверджень. Якщо твердження доведено, то всі лінії, які приймають участь у даному твердженні, утворюють необхідний символ. Можна формулювати допоміжні твердження на елементарних поняттях, для того, щоб простіше було представляти об’єкти, з яких вони складаються. Наприклад: паралельні (…), кут_приблизно_180 (…), поворот_вправо (…), крапка_на_лінії (…), тощо. Базове поняття лінії, на якому побудовано більшість тверджень, також розкладається на елементарні.
Лінія – це послідовність окремих відрізків, які з’єднані, і в місці їх з’єднання утворюють кут приблизно 180 градусів (див. програму).
Роспізнати_букву:-
лінія(X1,Y1, X2,Y2), лінія(X2,Y2, X3,Y3),
лінія(X4,Y4, X5,Y5),X4<X5, not(лінія(X1,Y1, X3,Y3)),
крапка_на_лінії(X4,Y4, X1,Y1,X2,Y2),
крапка_на_лінії(X5,Y5, X2,Y2,X3,Y3),
паралельні(X1,Y1,X3,Y3, X4,Y4,X5,Y5),
write("буква А:", X4,Y4, X5,Y5, X1,Y1,X2,Y2,X3,Y3),fail.
Роспізнати_букву:-
Дуга_вправо(X1,Y1, X2,Y2, X3,Y3, X4,Y4),
not(лінія(X1,Y1, якась_координата_X1, якась_координата_Y1)),
not(лінія(X4,Y4, якась_координата_X2, якась_координата_Y2)),
write("буква С:", X1,Y1, X2,Y2, X4,Y4),fail.
;-------------------------------------------------------------------------
вектор(8,7, 6,9). вектор(4,3, 3,5). вектор(1,12, 6,9). вектор(3,5, 6,9).
вектор(1,12,3,5). вектор(7,11,5,13). вектор(6,17,5,15). вектор(7,11, 9,10).
вектор(11,11, 12,13). вектор(5,15, 5,13). вектор(9,10, 11,11).
вектор(15,15, 13,14). вектор(7,18, 9,17). вектор(13,19, 11,17).
вектор(10,22, 15,17). вектор(9,17, 11,17). вектор(15,15, 15,17).
вектор(14,10, 12,2). вектор(17,9, 13,6). вектор(16,2, 13,6).
вектор(18,2, 20,9). вектор(23,3, 20,9). вектор(19,5, 22,5).
вектор(27,3, 27,10). вектор(25,10, 29,10). вектор(25,6, 29,6).
вектор(25,10, 24,8). вектор(29,10, 30,8).
вектор(25,6,24,8). вектор(29,6,30,8). вектор(31,9,31,2). вектор(31,9,34,9).
вектор(33,6,31,6). вектор(34,2,31,2). вектор(36,5,36,4). вектор(37,2,36,4).
вектор(36,5,37,7). вектор(37,2,39,2). вектор(38,8,37,7).вектор(38,8,39,8).
вектор(39,2, 40,4). вектор(40,7, 39,8). вектор(40,10, 40,4).
вектор(40,10,39,12). вектор(37,12, 39,12). вектор(37,12, 35,11).
вектор(32,18, 35,17). вектор(32,18, 32,20). вектор(35,17, 35,15).
вектор(35,15, 34,14). вектор(32,20, 33,21). вектор(33,21, 34,21).
вектор(34,14, 33,14). вектор(32,15, 33,14). вектор(34,21, 35,20).
вектор(32,15, 32,16). вектор(37,22, 37,16). вектор(39,14, 40,15)
вектор(38,14, 37,16). вектор(39,14, 38,14). вектор(36,19, 39,19).
вектор(20,13, 20,20). вектор(20,13, 28,13). вектор(28,20, 20,20).
вектор(30,15, 30,22). вектор(28,20, 30,22). вектор(28,13, 28,20).
вектор(22,22, 30,22). вектор(28,13, 30,15). вектор(20,20, 22,22).
вектор(22,15, 24,18). вектор(22,15, 24,16). вектор(22,15, 26,15).
вектор(24,18, 24,16). вектор(24,18, 26,15). вектор(26,15, 24,16).
вектор(1,17, 7,25). вектор(1,17, 1,25). вектор(1,25, 7,25).
вектор(1,21, 4,21). вектор(1,21, 4,25). вектор(4,25, 4,21).
;-------------------------------------------------------------------------
відрізок(X1,Y1, X2,Y2):- вектор(X1,Y1, X2,Y2).
відрізок(X1,Y1, X2,Y2):- вектор(X2,Y2, X1,Y1).
лінія(X1,Y1, X2,Y2):- відрізок(X1,Y1, X2,Y2).
лінія(X1,Y1, X3,Y3):- відрізок(X1,Y1, X2,Y2), лінія(X2,Y2, X3,Y3),
кут_приблизно_180(X1,Y1, X2,Y2, X3,Y3).
кут_приблизно_180(X1,Y1, X2,Y2, X3,Y3):-
знаходимо_квадрати_сторін_трикутника(X1,Y1, X2,Y2, X3,Y3, A,B,C),
A<C,B<C,знаходимо_квадрат_косинуса_кута_C(A,B,C,cos), cos>90.
; 1=100, більше 90 означає що косинус більше 0,9 У зв’язку з тим,що це цілі числа.
крапка_на_лінії(X3,Y3, X1,Y1,X2,Y2):- ;перша координата - це крапка,а друга це лінія.
кут_приблизно_180(X1,Y1, X3,Y3, X2,Y2).
квадрат_довжини_лінії(X1,Y1, X2,Y2, S):-
L1=X1-X2, L2=Y1-Y2, S1=L1*L1, S2=L2*L2, S=S1+S2.
знаходимо_квадрати_сторін_трикутника(X1,Y1, X2,Y2, X3,Y3, A,B,C):-
квадрат_довжини_лінії(X1,Y1, X2,Y2, A),
квадрат_довжини_лінії(X2,Y2, X3,Y3, B),
квадрат_довжини_лінії(X1,Y1, X3,Y3, C).
; 180:cos=99, 153:cos=80, 135:cos=50, 127:cos=36, 117:cos=20, 90: cos=0
знаходимо_квадрат_косинуса_кута_C(A,B,C,cos):- P1=A+B, P2=P1-C,
P5= A*B, P3= P2*P2, P0=25, P4=P0*P3, P4 = cos*P5.
паралельні(X1,Y1,X2,Y2, X3,Y3,X4,Y4):-
VX=X2-X3, VY=Y2-Y3, X5=X4+VX, Y5=Y4+VY,
знаходимо_квадрати_сторін_трикутника(X1,Y1, X2,Y2, X5,Y5, A,B,C),
знаходимо_квадрат_косинуса_кута_C(A,B,C,cos), cos>90.
; Якщо першу лінію приєднати до другої лінії, то кут між ними буде приблизно 180 (згідно теореми косинусів).
;на основі, що за теоремою Піфагора кут більший 90 градусів.
поворот_вправо(X1,Y1,X2,Y2,X3,Y3):- P1=Y3-Y2, P2=X2-X1, P3=X3-X2,
P4=Y2-Y1, Q1=P1*P2, Q2=P3*P4, Q1<Q2.
Дуга_вправо(X1,Y1, X2,Y2, X3,Y3, X4,Y4):- відрізок(X1,Y1, X2,Y2),
відрізок(X2,Y2, X3,Y3), поворот_вправо(X1,Y1,X2,Y2,X3,Y3),X4=X3,Y4=Y3,
знаходимо_квадрати_сторін_трикутника(X1,Y1, X2,Y2, X3,Y3, A,B,C),
P=A+B,C>P,
знаходимо_квадрат_косинуса_кута_C(A,B,C,cos),cos>35.
; дуга вправо - це такий поворот, кут якого більший 120 градусів.
Дуга_вправо(X1,Y1, X2,Y2, X3,Y3, X4,Y4):- відрізок(X1,Y1, X2,Y2), Дуга_вправо(X2,Y2, X3,Y3, XX,YY, X4,Y4), поворот_вправо(X1,Y1,X2,Y2,X3,Y3),
знаходимо_квадрати_сторін_трикутника(X1,Y1, X2,Y2, X3,Y3, A,B,C),
P=A+B,C>P, знаходимо_квадрат_косинуса_кута_C(A,B,C,cos),cos>35.
; Послідовність дуг, які завертають вправо, кут між якими не менший ніж 120 градусів.
приблизно_однакові(S1, S2):- K1=10, K2=9, P1=S1*K1, P2=S2*K2, P1>P2, P3=S2*K1, P4= S1*K2, P3>P4.
Завдання 1. Відкоректувати твердження для букви «С», щоб програма її вірно визначала на основі твердження, що відстань між краями ліній помножена на 2 повинна бути менша ніж довжина кривої лінії.
Завдання 2. Знайти свій варіант розпізнавання символу, заданого викладачем.
ЗМІСТ
 2018-02-13
2018-02-13 496
496








