Теоретические основы квантовой механики

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

 

Кафедра общей и технической физики

 

 

Общая физика

Квантовая механика

 

Методические указания к расчётно-графическим работам и варианты заданий для студентов всех специальностей

 

 

САНКТ-ПЕТЕРБУРГ

2012

УДК 531/534 (075.83)

 

Общая физика. КВАНТОВАЯ МЕХАНИКА. Методические указания к расчётно-графическим работам и варианты заданий для студентов всех специальностей. А.С. Мустафаев, Т.В. Стоянова. Национальный минерально-сырьевой университет «Горный». СПб, 2012. 26 с.

ISBN 5-94211-162-6

 

 

Расчётно-графические работы предназначены для студентов всех форм обучения национального минерально-сырьевого горного университета. Выполняются индивидуально в соответствии с вариантом.

 

Научный редактор

 

 

Ó  Национальный минерально-сырьевой университет «Горный»,2012 г.

 

 

ВВЕДЕНИЕ

 

Вопросы и задачи, содержащиеся в пособие охватывают большую часть стандартного курса квантовой механики, изучаемого в технических вузах и способствуют более глубокому усвоению теоретического материала данного раздела.

 

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ РАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ

Выполнение расчётно-графической работы предполагает достаточно большой объём самостоятельной работы студента. 

Перед выполнением расчётно-графической работы рекомендуется изучить лекционный курс на тему «элементы квантовой механики» и познакомиться с соответствующим разделом учебника общего курса физики. Если при самостоятельном изучении теоретического материала возникли вопросы, желательно обсудить их на практических занятиях, но если и после этого остались не ясные моменты можно получить индивидуальную консультацию преподавателя, ведущего расчётно-графическую работу или лектора.

При изучении физического явления, прежде всего, необходимо выяснить сущность явления, условия при которых оно возможно, определить с помощью каких физических величин, оно характеризуется. Желательно понять, как оно связано с другими явлениями и возможности его применения на практике. При определении физической величины важно обратить внимание на то, какая это величина – скалярная или векторная, какие свойства она характеризует, выяснить её размерность и формулу, определяющую связь с другими физическими величинами. При прочтении закона обратите внимание на границы его применения, определите, между какими явлениями он выражает связь, уточните формулировку и математическое выражение закона.

Расчётно-графическая работа оформляется на компьютере.

Прежде чем приступить к выполнению практической части расчётно-графической работы необходимо ознакомиться с требованиями, размещенными на сайте Горного университета. На титульном листе указать: название института, наименование дисциплины, название работы, фамилию и инициалы студента и ведущего расчётно-графическое задание преподавателя, год выполнения работы.

Необходимо полностью переписать задачу своего варианта, а заданные физические величины выписать отдельно, при этом все числовые значения должны быть переведены в одну систему единиц. При получении расчётной формулы приведите её полный подробный вывод.

Математическое решение должно сопровождаться пояснениями, а в случае необходимости его можно продемонстрировать рисунком. Задачу рекомендуется решить сначала в общем виде (в буквенных обозначениях), поясняя применяемые при написании формул буквенные обозначения, и только после проверки размерности искомой физической величины, подставить в выведенную формулу числовые значения. Все необходимые числовые значения величин должны быть выражены в системе «СИ». После получения окончательного результата, для удобства построения графических зависимостей можно перейти к вне системным единицам. Например, выразить энергию в электрон-вольтах.

Перед построением графиков необходимо получить аналитическое выражение функциональной зависимости. Выбрать удобный масштаб и указать его на осях координат, а так же физические величины и единицы измерения.

На координатной плоскости обязательно должны быть нанесены экспериментальные точки. Кривая, аппроксимирующая функциональную теоретическую зависимость строится в соответствии с методом наименьших квадратов.

 

 

Содержание отчёта (Форматировал)

1.Титульный лист

2. Теоретическая часть:

2.1.Определения всех физических явлений, законов и величин, встречающихся в данной работе.

2.2.Основные расчётные формулы с пояснениями.

3. Расчётная часть:

3.1.Задание с исходными данными своего варианта.

3.2.Расчёт с пояснениями

3.3.Графики.

3.4.Анализ результатов. Заключение.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ

Уравнение Шредингера - основное уравнение нерелятивистской квантовой механики является уравнением относительно волновой функции.

Для описания распределения вероятности нахождения частицы в данный момент времени в некоторой точке пространства, вводят волновую функцию (или пси-функцию) - .

Физический смысл имеет не сама волновая функция, а квадрат её модуля: , где  - функция, комплексно сопряжённая с самой волновой функцией.  - плотность вероятности, определяющая вероятность пребывания электрона в данной точке пространства:

Вероятность  того, что частица находится в элементе объёма dV, равняется произведению квадрата модуля волновой функции  и элемента объёма dV:

                       

Волновая функция удовлетворяет условию нормировки вероятностей:

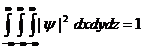                              (1)

это означает, что пребывание частицы где-либо в пространстве, есть достоверное событие и его вероятность равна 1.

Основные свойства волновой функции:

1) функция конечна (вероятность не может быть больше 1); однозначна (вероятность не может быть не однозначной величиной); непрерывна (вероятность не может изменяться скачком).

2) производные  должны быть непрерывны;

3) Функция  должна быть интегрируема, т.е. интеграл:

должен быть конечным.

Уравнение Шредингера - не выводится, а постулируется из оптико-механической аналогии.

 Уравнение Шредингера имеет вид:

                     (2)

где т -масса частицы, =D - оператор Лапласа (),    i - мнимая единица, градиент функции U, взятый с обратным знаком, определяет силу, действующую на частицу. Это уравнение часто называют временным, так как оно содержит производную по времени.

При условии, что поле, в котором движется частица стационарно – U - потенциальная энергия частицы в силовом поле, в котором частица движется. В этом случае решение уравнения Шредингера можно разделить на два множителя:

первый - зависит только от координат, второй - зависит только от времени.

                          (3)

Е – полная энергия частицы в стационарном поле и равная const.

Подставим (3) в (2), тогда:

Сократив, на общий множитель  получим:

           

Полученное уравнение называется уравнением Шредингера для стационарных состояний. Если перенести  в левую часть и разделить его на 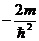, то получим уравнение в виде:

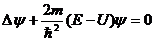                           (4)

где Е - полная энергия частицы, U - потенциальная энергия (силовое поле в котором движется частица, не зависящее от времени). 

Функции , удовлетворяющие уравнению Шредингера при данном U, называются собственными функциями.

Значения Е, при которых существуют решения уравнения Шредингера, называются собственными значениями.

Совокупность собственных значений называется спектром величины.

Квантование энергии

В случае дискретного спектра собственные значения и собственные функции можно пронумеровать:                       

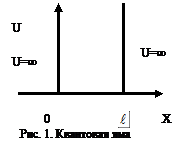
Найдём собственные значения энергии и соответствующие им собственные функции для более простого случая - для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

Пусть частица движется вдоль оси х, а её движение ограничено непроницаемыми стенками с координатами 0 и .

Тогда потенциальная энергия U равна нулю при  и обращается в бесконечность при х<0 и x> .

Так как волновая функция зависит только от координаты х, то стационарное уравнение Шредингера можно взять в виде:

Вероятность обнаружения частицы вне ямы равна нулю и значение волновой функции за пределами ямы равно нулю:

                                      (5)

В области  уравнение имеет вид:          

так как U=0. Пусть: 

                              (6),

тогда это уравнение можно записать в виде:

Это уравнение известно из теории колебаний и его решение имеет вид:

                   (7)

Условия (5) выполняются при соответствующих k и . Из условия получаем:

Следовательно, =0. Из условия  следует, что:       

    (8).

где n=1,2,3

Если n=0, то получается, что частица нигде не находится, поэтому этого не может быть. Исключив k из уравнений (6) и (8) найдём собственные значения энергии частицы:

   

,

тогда энергия частицы в квантовой яме:

 (n=1,2,3,….,) где - ширина квантовой ямы, а n - квантовое число, определяющее квантовые уровни частицы.

Разность энергий двух соседних уровней равна:

.

При больших квантовых числах выводы и результаты квантовой механики соответствуют классическим результатам.

Подставив в (7) k полученное из (8), найдём собственные значения функции задачи:

Для нахождения воспользуемся условием нормировки:        

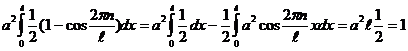
 Тогда получим: ,  и собственная функция имеет вид:

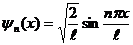(n=1,2,3,…)                       (9)