Рассмотрим знакоположительный числовой ряд 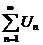 , где
, где 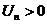 .Последовательность частичных сумм такого ряда будет всегда возрастающей:
.Последовательность частичных сумм такого ряда будет всегда возрастающей:
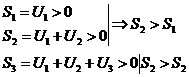
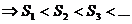
На 1 курсе была доказана теорема о том, что: монотонно возрастающая последовательность, ограниченная сверху имеет конечный предел.
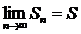 - число.
- число.
Для знакоположительного ряда достаточно доказать, что, последовательность частичных сумм 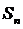 ограничена сверху числом (возрастание и так есть).
ограничена сверху числом (возрастание и так есть).
1й признак сравнения
Дано 2 ряда с положительными членами 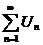 (1) и
(1) и 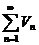 (2) и начиная с некоторого номера N выполняется неравенство
(2) и начиная с некоторого номера N выполняется неравенство 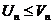 , тогда если (2) сходится то и (1) сходится. Если (1) расходится то и (2) тоже расходится, (ряд меньший сходящегося тоже сходится, ряд больший расходящегося тоже расходится).
, тогда если (2) сходится то и (1) сходится. Если (1) расходится то и (2) тоже расходится, (ряд меньший сходящегося тоже сходится, ряд больший расходящегося тоже расходится).
Доказательство: Обозначим через 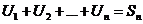 - n – частичная сумма 1 ряда и
- n – частичная сумма 1 ряда и 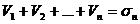 - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
Т.к 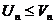
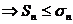 . Пусть 2 ряд сходится, тогда
. Пусть 2 ряд сходится, тогда 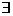
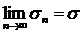 , причём
, причём  ограничена сверху числом
ограничена сверху числом 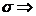 (1) сходится.
(1) сходится.
Пусть 1 ряд расходится 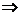
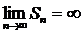 , т.к
, т.к 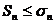
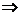
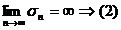 расходится.
расходится.
Конец доказательство.
Замечание: при доказательстве этого признака мы считали, что неравенство 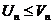 выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
Для сравнения необходим стандартный набор рядов, о сходимости всё известно. К таким рядам относятся:
| Ряды для сравнения: | |
Ряды членов геометрической прогрессии:
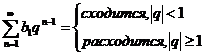
| Обобщенно гармонический ряд:
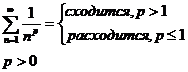 (строгое доказательство будет проведено после интегрального признака сходимости)
(строгое доказательство будет проведено после интегрального признака сходимости)
|
Примеры:
1) 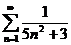
2) 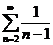
3) 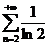
 2018-02-14
2018-02-14 174
174








