Главный фокус сферического зеркала

Пусть точка 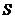 находится очень далеко от точки , так что

.

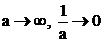Тогда из формулы сферического зеркала запишем:

.

Изображения (точка 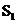) будет находиться в точке, расстояние до которой от зеркала равно

.

Эту точку называют главным фокусом зеркала и обозначают буквой .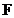

Расстояние главного фокуса от зеркала 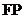 называется фокусным расстоянием сферического зеркала и обозначается также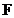

.

Формулу сферического зеркала можно теперь записать в виде

.

Лучи, падающие на зеркало из точки , находящейся бесконечно далеко от зеркала можно считать параллельными. Поэтому ход лучей имеют вид.

Пусть пучок параллельных лучей падает на сферическое вогнутое зеркало параллельно  побочной оптической оси. Отраженные лучи сойдутся в некоторой точке , принадлежащей плоскости проходящей через фокус зеркала перпендикулярно главной оптической оси. Эта плоскость называется фокальный плоскостью зеркала.

Из обратимости световых лучей следует, что если поместить точечный источник света в главный фокус 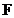 или в любую точку  фокальной плоскости, то после отражения от сферической поверхности получится параллельный пучок световых лучей.