2018-02-14
290
Пластинка имеет вид клина с очень малым углом 
.
Плоская световая волна падает нормально на поверхность клина. Вследствие малости угла можно считать, что волна падает нормально к обеим поверхностям. Пусть при отражении в точках 1 и 
для отраженных лучей выполняется условие максимума интенсивности, а лучи, отраженные в точках 2 и 
создают также максимум интенсивности. Обозначим толщину клина между точками 1 и через 
, а толщину между точками 2 и через 
.
Найдем оптическую разность хода для этих точек.
,
, 
, 
.
.
Аналогично для точек 2 и
,
где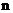 
- абсолютный показатель преломления вещества клина.
При отражении в точках 1 и 2 выполняется условие
.
При отражении в точках и , соответственно
.
Следовательно, при отражении в точках 1 и 2 возникает скачок фазы на 
, который учтем, отнимая от оптической разности хода 
. Запишем условие для максимумов интенсивности
,
где 
- номер максимумов.
,
,
. 
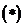
Обозначим:
.
- расстояние между интерференционными максимумами с номерами 
и 
.
Из прямоугольного треугольника запишем:
.
Подставим в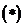
,
,
.
Пусть в точках 1 и 2 соседние максимумы
,
,
где - расстояние между соседними максимумами.
П.3. Кольца Ньютона.
Плосковыпуклая линза с большим радиусом кривизны 
лежат, касаясь выпуклой стороной плоской стеклянной поверхности. Между линзой и поверхностью существует зазор с переменной толщиной 
. Параллельный пучок света нормально падает на плоскую поверхность линзы. При этом вследствие большого радиуса кривизны лучи падают практически нормально на верхнюю границу зазора.
Отражения от верхней и нижней границ зазора лучи интерферируют и возникают чередующиеся яркие и темные кольца, которые называются кольцами Ньютона. Прямая 
называется осью системы. Расстояние от точек кольца Ньютона до оси называется радиусом кольца Ньютона.
Обозначим радиус кольца Ньютона 
. Запишем
,
,
,
,
.
Для наблюдения интерференции необходимо, чтобы выполнялось условие
, 
.
Следовательно,
,
.
Пусть в зазоре находится прозрачное вещество с абсолютным показателем преломления 
. Обозначим показатель преломления стекла линзы и пластины 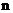. Пусть выполняется условие
.
Оптическая разность хода лучей равна
.
При отражении от верхней границы скачка фазы не возникает, т.к. 
, но при отражении от нижней границы зазора скачок фазы возникает, т.к. . Следовательно, при записи условий максимумов и минимумов необходимо учесть дополнительную разность фаз лучей, равную . Для этого к оптической разности хода прибавляют .
Для максимума интенсивности
, 
,
,
,
, 
Величина 
называется радиусом светлого кольца Ньютона с номером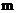 
.
Для минимума интенсивности
,
,
где 
- радиус темного кольца Ньютона с номером .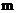
Просветление оптики.
На поверхность стекла с показателем преломления 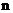наносится тонкая пленка толщиной . При этом показатель преломления пленки равен
.
При нормальном падении света возникает два отражения луча.
Найдем условие, при котором эти лучи интерферируют так, что возникает минимум интенсивности. Оптическая разность хода лучей равна
.
Рассмотрим условия отражения от верхней и нижней границ пленки.
Верхняя граница:
, 
.
Нижняя граница
.
Отражение происходит в одинаковых условиях так, что при отражении каждого луча возникает скачок фазы на , но дополнительной разности фаз колебаний между лучами не возникает.
Следовательно, условие минимума интенсивности
, 
,
,
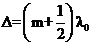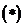
Запишем
.
При выполнении условий минимума 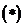и соотношения
.
Интенсивность отраженных волн оказывается минимальной и равной 0
.
Следовательно,
.
Световая волна проходит в систему без потери энергии вследствие отражения.
