Многолучевая интерференция

В математике известно, что гармоническую функцию можно представить как вещественную часть комплексной функции

,

где  - мнимая единица.

При выполнении над комплексными функциями операции сложения, дифференцирования и интегрирования вещественная часть результата совпадает с результатом, который получился бы при выполнении аналогичных операций над вещественными частями тех же функций. В то же время вычисления с экспонентами значительно проще, чем с тригонометрическими функциями.

Пусть в точку 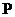 приходит  световых волн, которые возбуждают колебания

,

,

,

.

Результирующее колебание в точке 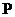 равно

.

Сумма представляет собой сумму членов геометрической прогрессии с множителем

,

.

Обозначим

.

Величина  называется комплексной амплитудой. Найдем квадрат амплитуды

.

Интенсивность:

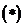
- интенсивность колебаний возбуждаемых в точке 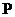 одной световой волны.

- интенсивность колебаний, возбуждаемых в точке 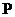всеми  световыми волнами.

 - отставание по фазе для световых волн от соседних источников.

Пусть все колебания приходят в одной фазе, т.е.

Выражение 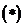 становится неопределенным: . Раскрываем неопределенность по правилу Лопиталя, дважды дифференцируя по . Получим

,

.

Очевидно, что для амплитуды колебаний:

.