Розробка вирішувача рівнянь МДО
Цель работы: Ознакомиться с разновидностями методов численного решения дифференциальной системы уравнений, изучить алгоритм нахождения решений методом Эйлера. Разработать программу решателя уравнений для заданного сетевого объекта.
Введение
В прошлой лабораторной работе был реализован генератор уравнений, с помощью которого были подготовлены все вспомогательные данные для решения системы уравнений следующего вида (6):
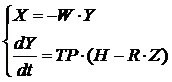
Матрицы W и TP, диагональная матрица коэффициентов аэродинамического сопротивления R, а также вектор-столбец Н рассчитаны и известны. Можно переходить к решению системы, состоящей из линейных и дифференциальных уравнений.
Решение дифференциальных уравнений
Обыкновенное дифференциальное уравнение (ОДУ) – это дифференциальное уравнение вида F(t,x,x′,x′′,…,x(n)) = 0, где x(t) –неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от переменной t, штрих означает дифференцирование по t. Число n называется порядком дифференциального уравнения.
Если все дополнительные условия задаются в одной точке x0, то совокупность ОДУ и дополнительных условий называются задачей Коши для рассматриваемого ОДУ. В этом случае дополнительные условия называют начальными условиями. Если начальные условия задают более чем в одной точке, то совокупность ОДУ и дополнительных условий называют краевой задачей Коши, а дополнительные условия называют граничными или краевыми условиями.
Методы решения ОДУ бывают одношаговыми и многошаговыми.
Одношаговые методы – методы решения диф. уравнений, в которых для нахождения решения в некоторой точке отрезка xn+1 используется информация о решении задачи только на отрезке [xn, xn-1] длиной в один шаг. К классическим одношаговым методам относят метод Эйлера, метод Рунге-Кутта.
Многошаговые методы обладают более высокой точностью расчета решений. Повышение точности вычислений осуществляется за счет использования решений на предыдущих шагах. Наиболее известными среди многошаговых методов являются явные (экстраполяционные) и неявные (интерполяционные) методы Адамса [10, 24]. Явный метод Адамса еще называют методом Адамса-Башфорта.
В данной лабораторной работе для расчета дифференциальных уравнений и нахождения вектора Y будет использоваться самый простой численный метод – метод Эйлера.
Метод Эйлера
Пусть решение разыскивается на интервале [ t 0, b). На этом интервале введем узлы t0 < t1< … <tn ≤ b.
Тогда приближенное решение yi в узлах xi определяется по формуле:
Ui = Ui-1 + (ti-ti-1)∙F(ti-1,Ui-1), i = 1,2,…,n
или
Ui = Ui-1 + h∙F(ti-1, Ui-1)
где Ui-1 – приближенное значение в точке ti-1,
h – величина шага сетки по t,
F (ti-1, Ui-1) – правая часть уравнения, вычисленного в точке ti-1.
Общий алгоритм итерационного решения с помощью метода Эйлера приведен на рисунке 3.1.
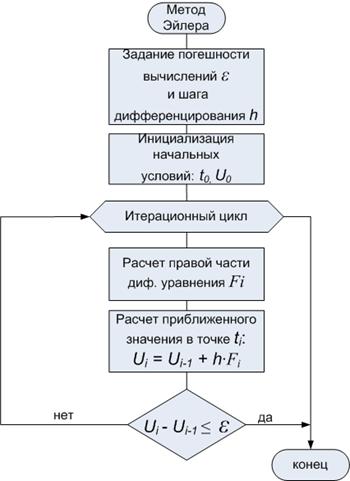
Рис 3.1 Общий алгоритм метода Эйлера
Теперь, исходя из формулы метода Эйлера, можно изобразить алгоритм решателя системы уравнений, который будет искать векторы неизвестных X и Y (рис. 3.2).
В начале алгоритма необходимо определить начальные условия для численного метода. Чем точнее будет задано начальное значение в первой точке, тем точнее будут рассчитаны последующие. Так как метод Эйлера является самым простым и неточным численным методом, точность расчета будет зависеть от точности начальных условий и от величины шага дифференцирования. Для расчета значений воздушных потоков в сетевых объектах в качестве начальных значений допустимо использовать нули или близкие к ним значения. Величина шага h может колебаться в пределах от 0.1 до 1∙10-4.
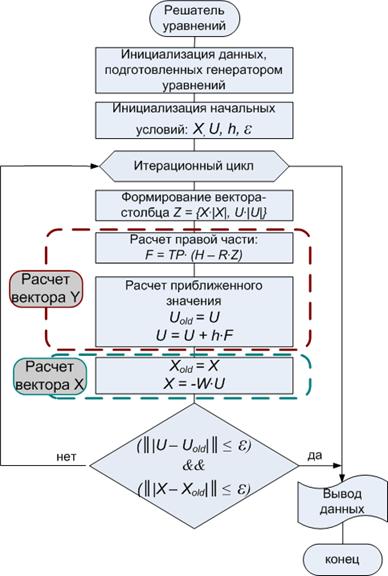
Рис 3.2 Алгоритм работы решателя уравнений
Выход из итерационного метода осуществляется по условию, определяющему разницу между приближенными значениями на текущем и предыдущем шагах. Если абсолютная разность воздушных потоков │U[i] – Uold[i]│ и │ X[j] – Xold[j]│ в i -ых ветвях антидерева и j -ых ветвях дерева меньше или равна заданной точности ε, то итерационный цикл можно завершать, так как завершился переходной процесс и воздушные потоки перешли в установившийся режим. Завершение расчетов должно осуществиться только после выполнения данного условия для каждой ветви графа, т.е. после того, как воздушный поток в каждой ветви сети достигнет установившегося значения. Одним из самых простых способов проверки является прямой перебор каждого из условий, т.о. количество условий будет равно количеству ветвей m в графе. Однако в случае наличия графа больших размерностей данный способ проверки приводит к достаточно громоздкой реализации алгоритма.
Вторым наиболее рациональным и распространенным способом является использование алгоритма нахождения нормы вектора (или матрицы).
Норма вектора — скаляр, дающий представление о величине элементов вектора. Обозначим через x = (x1, x2, …, xm)T точное решение системы, а через x* = (x1*, x2*, …, xm*)T – приближенное решение системы. Для количественной характеристики вектора погрешности ε = x – x* введем понятие нормы.
Нормой вектора x называется число ║ x ║, удовлетворяющее трем аксиомам:
1) ║ x ║≥ 0, причем ║ x ║= 0 тогда и только тогда, когда ║ x ║= 0;
2) ║α x ║ = │α│∙║ x ║для любого вектора x и любого числа α;
3) ║ x + y ║ ≤ ║ x ║+║y║ для любых векторов x и y.
Наиболее употребительными являются следующие три нормы:
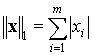 ,
,
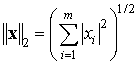 ,
,
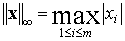 .
.
Результатом работы программы решателя уравнений является визуализация рассчитанных значений воздушных потоков, т.е. построение графиков Qi(t) (рис. 3.3).
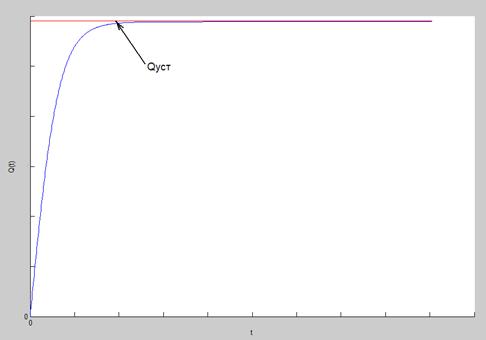
Рис 3.3 Ожидаемые результаты моделирования
Проверка результатов в среде Matlab
Самым простым способом проверки результатов работы разработанной на языке С программы как генератора, так и решателя уравнений, является составление m-файла и запуск его в среде Matlab.
Ниже приведен код подобного m-файл а с комментариями, в котором реализованы алгоритмы генератора и решателя уравнений для графа вентиляционной сети, рассмотренного в лабораторной работе №1 (рис. 1.1б). Для запуска скрипта необходимо в окне редактора программы нажать F5.
На рисунках 3.4 и 3.5 изображены результаты работы данного Matlab- скрипта.
function NetworkSimulation()
%%---------------------------------Initial Data------------------------
H = [0 0 0 0 0 0 0 4100 0]'; %%Формирование вектора-столбца Н, отсортированного по ветвям дерева/антидерева
Ax = [ -1 0 0 -1 0;
1 -1 0 0 0;
0 0 0 1 -1;
0 1 -1 0 0;
0 0 0 0 1;
];
Ay = [ 0 0 1 0;
-1 0 0 0;
0 -1 0 0;
1 0 0 0;
0 1 0 -1;
];
Sx = [ 0 1 0 0 0;
0 0 0 0 1;
1 1 1 0 0;
1 1 1 -1 -1;
];
Sy = [-1 0 0 0;
0 -1 0 0;
0 0 1 0;
0 0 0 -1;
];
Rx = [ 1.35 0 0 0 0;
0 1.98 0 0 0;
0 0 1.35 0 0;
0 0 0 1.34 0;
0 0 0 0 2.17;
];
Ry = [ 2.32 0 0 0;
0 2.677 0 0;
0 0 1.53 0;
0 0 0 3.35;
];
Kx = [ 301 0 0 0 0;
0 342 0 0 0;
0 0 500 0 0;
0 0 0 298 0;
0 0 0 0 149;
];
Ky = [ 127 0 0 0;
0 347 0 0;
0 0 263 0;
0 0 0 103;
];
S = [Sx Sy]; %%Формирование матрицы S, отсортированной по ветвям дерева/антидерева
R = blkdiag(Rx,Ry); %%Формирование диагональной матрицы R, отсортированной по ветвям дерева/антидерева
global N_Tree N_ATree;
N_Tree = 5;%% Количество ветвей дерева
N_ATree = 4; %% Количество ветвей антидерева
%%--------------------------------------------------------------------
%% Генератор уравнений
%%--------------------------------------------------------------------
W = inv(Ax)*Ay %% нахождение матрицы W и вывод ее на экран
TP = inv(Sy*Ky - Sx*Kx*W)*S %% нахождение матрицы W и вывод ее на экран
%%--------------------------------------------------------------------
%% Решатель уравнений. Реализация метода Эйлера
%%--------------------------------------------------------------------
global step iter;
step = 0.1; %% шаг дифференцирования
eps = 0.01; %% погрешность вычислений
iter = 0;
%%-------- Задание начальных значений для метода Эйлера
%% Создаются векторы-столбцы U, Uold, F, X, Xold, каждый элемент которых
%% присваивается значению переменной init_value
init_value = 0.001;
U(1:N_ATree,1) = init_value; %% i.e. U(1:4) = init_value; U';
Uold(1:N_ATree,1) = init_value;
F(1:N_ATree,1) = init_value;
X(1:N_Tree,1) = init_value;
Xold(1:N_Tree,1) = init_value;
%%--------------------------------------------------------------------
fid = Open_File(); %% Создаются файлы для сохранения результатов вычислений
vfig = PlotCreate(); %% Создаются графические окна для вывода графиков
%% Итерационный цикл
for i = 1:1000
iter = iter + 1;
Z = [X.*abs(X); U.*abs(U)]; %%Формирование вектора-столбца Z
F = TP*(H - R*Z); %% вычисление правой части F
Uold = U; %% Сохранение приближенного решения, полученного на предыдущем шаге
U = U + F*step; %% Нахождение следующего приближенного решения
Xold = X;
X = -W*U; %% Расчет ветвей дерева X
WriteToFile(fid, X, U); %% Сохранение расчетов в файлы
normU = norm(abs(U-Uold)); %% Расчет нормы вектора решений для ветвей антидерева
normX = norm(abs(X-Xold)); %% Расчет нормы вектора решений для ветвей дерева
if (normU<=eps)&&(normX<=eps)
break;
end
%% Вывод графиков Xi(t)
for i= 1:(N_Tree) PlotResults(vfig(1), X(i), Xold(i));end;
%% Вывод на экран (в командную строку)
if (mod(iter,50)==0)
str=sprintf('iteration: %u-th\t normX= %e\t normU = %e\n\n', iter, normX, normU);
disp(str)
end
end
%% Закрытие файлов
Close_File(fid);
%%Вывод результатов в командное окно
out = '';
for i= 1:N_Tree out = strcat(out,sprintf('\tX%d = %4.4f', i, X(i))); end;
for i= 1:N_ATree out = strcat(out,sprintf('\tY%d = %4.4f', i, U(i))); end;
disp(out)
% X1 = Q2, X2 =Q4, X3=Q8, X4=Q3, X5=Q6, Y1=Q5, Y2=Q7, Y3=Q1, Y4=Q9
% Q1 = Y3, Q2 = X1, Q3=X4, Q4=X2, Q5 =Y1, Q6=X5, Q7=Y2, Q8=X3, Q9=Y4
str=sprintf('\n\tQ1 = %4.4f \tQ2 = %4.4f \tQ3 = %4.4f \tQ4 = %4.4f \tQ5 = %4.4f \tQ6 = %4.4f \tQ7 = %4.4f \tQ8 = %4.4f \tQ9 = %4.4f', U(3), X(1), X(4), X(2), U(1), X(5), U(2), X(3), U(4));
disp(str)
end
%%--------------------------------------------------------------------
%%--------------------------------------------------------------------
function fig = PlotCreate()
title_str = {'Branches of tree', 'Branches of antitree'};
for i = 1:(1)
fig(i) = figure(); hold on;
title(title_str(i));
xlabel('t');
ylabel('Q(t)');
end;
end
%%--------------------------------------------------------------------
function PlotResults(fig, Q, Qold)
global step iter;
vt = [(iter-1)*step, iter*step];
vQ = [Qold, Q];
figure(fig), hold on;
plot(vt, vQ);
hold off;
end
%%--------------------------------------------------------------------
function WriteToFile(fid, X, U)
global step iter N_Tree N_ATree;
time = iter*step;
for i = 1:N_Tree fprintf(fid(i),'%d\t %8.8f \n',time, X(i)); end;
for i = 1:N_ATree fprintf(fid(N_Tree+i),'%d\t %8.8f \n',time, U(i)); end;
end
%%--------------------------------------------------------------------
function fid = Open_File()
global N_Tree N_ATree;
mkdir('NSresults'); %% создание каталога
for i = 1:N_Tree
fname = sprintf('NSresults/X%d.txt', i);
fid(i) = fopen(fname,'w');
end;
for i = 1:N_ATree
fname = sprintf('NSresults/Y%d.txt', i);
fid(N_Tree+i) = fopen(fname,'w');
end;
end
%%--------------------------------------------------------------------
function Close_File(fid)
global N_Tree N_ATree;
for i = 1:(N_Tree+N_ATree) fclose(fid(i)); end;
end
%%--------------------------------------------------------------------
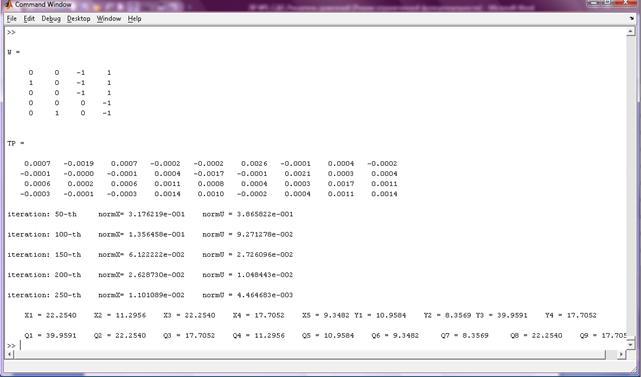
Рис 3.4 Полученные результаты расчетов
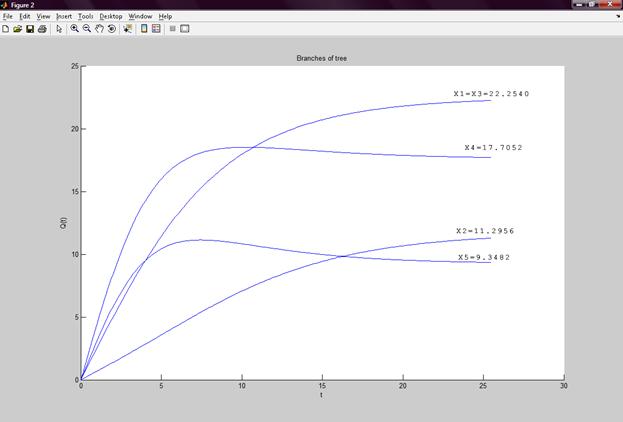
Рис 3.5 Расход воздушных потоков в ветвях дерева
 2018-02-14
2018-02-14 1523
1523







