Расчет частоты света, дифрагированного на ультразвуке

ПРИЛОЖЕНИЯ

 

Приложение 1

 

Таблица некоторых используемых в работе

Физических величин

 

Величина	Обозначение	Значение
Скорость света   в вакууме	с	3×108 м/c
Длина волны излучения гелий-неонового лазера	l	0,6328 мкм
Длины некоторых волн спектра излучения паров ртути	l1 l2 l3 l4	0,4358 мкм 0,5461 мкм 0,5770 мкм 0,5791 мкм
Постоянная Больцмана		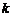1,38×10–23 Дж/К
Постоянная Стефана–Больцмана		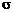5,67×10–8 Вт/(м2 ×К4)
Постоянная Планка	h	6,6×10–34 Дж×c
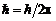
		1,05×10–34 Дж×c
Показатель преломления воздуха (l = 0,589 мкм, 0 °С, Р = 105 Па)	n в	1,000292

 

Приложение 2

 

К работе № 30

 

Сложение n  гармонических колебаний

одинаковой амплитуды а

С последовательным сдвигом по фазе на d

 

Определим вид функции, описывающей гармоническое коле­бание, являющееся суммой 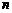 колебаний:

.

Для удобства расчетов перейдем к экспоненциальной форме за­писи гармонических колебаний:

.

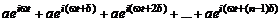Соответствующая сумма 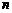 слагаемых имеет вид

.

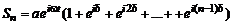Выражение, стоящее в скобках, является геометрической про­грессией. Поэтому

.

Если воспользоваться известным в математике выражением

,

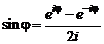то получим

.

 

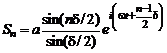Перейдем теперь от комплексной формы записи к исходной, дей­ствительной форме. Тогда результирующее гармоническое коле­бание будет иметь вид:

.

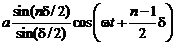Амплитуда такого колебания

.

 

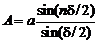Приложение 3

 

К работе № 32

 

Расчет частоты света, дифрагированного на ультразвуке

 

Ультразвуковая дифракционная решетка не является непод­виж-ной. Она перемещается со скоростью звука . В этом случае вторичные источники света в плоскости решетки под­вижны и поэтому должен проявляться эффект Доплера, заклю­чающийся в том, что частота наблюдаемого света 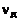 отличается от частоты излучаемого света . Этот эффект описывается фор­мулой

 ,                                      (1)

где 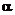 – угол между линией наблюдения и направлением движения источника, измеренным в системе координат, связанной с наблюдателем, .

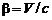Так как , то

.                       (2)

Угол 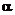 можно выразить через угол дифракции :

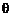.                                      (3)

Тогда . Следовательно,   

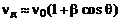.                                (4)

Из условия дифракционных максимумов при дифракции света на ультразвуке     

, m = 0; ±1; ±2 …,

следует, что 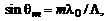  где 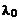 – длина волны падающего света. Если учесть, что , , 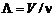то

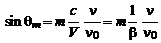.                            (5)

Подставив выражение (5) в выражение (4), получим

.                       (6)

 

О П Т И К А