Мектепішілік олимпиада

№ 8 есеп.

қосындысын табыңдар.

Шешуі: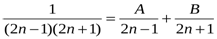

.

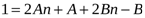
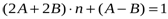
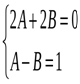
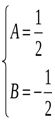
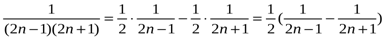
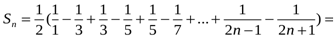
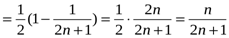Жауабы: .

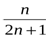№ 9 есеп.

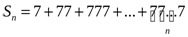қосындысын табыңдар.

Шешуі: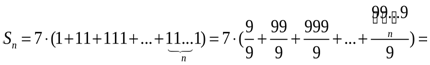

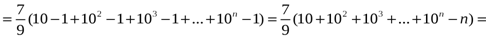
Жауабы: .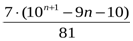

 

№ 10 есеп.

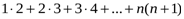қосындысын табу керек.

Шешуі: .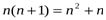

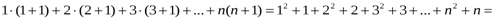
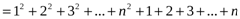, мұнда

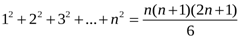тепе-теңдігі математикалық индукция әдісімен дәлелденген (68 бет 2-мысал), ал .

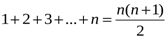Сонда

.

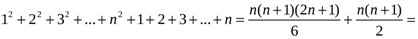
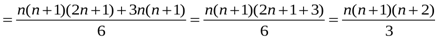Жауабы: .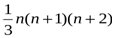

 

 

№ 11 есеп.

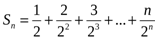қосындысын табыңдар.

Шешуі:

 

.

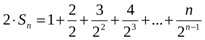
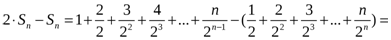
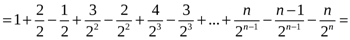
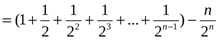
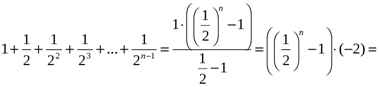
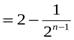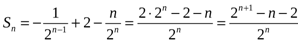
Жауабы: .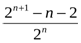

№ 19 есеп.

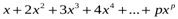қосындысын есептеңдер, .

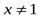Шешуі:

.

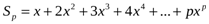
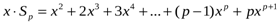
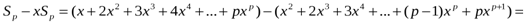
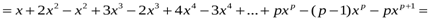
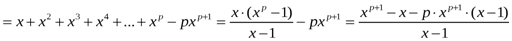
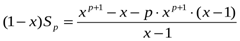
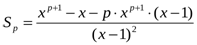Жауабы: .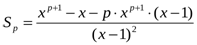

 

 

Аудандық олимпиадада берілген есептер:

Сынып.

№ 1.Кез-келген n натуралсаны үшін n(n²-1)(5n+2) өрнегінің 24-ке бөлінетіндігін дәлелдеңдер.

Дәлелдеуі: 5n+2=(5n+10)-8 теңдігін ескеріп өрнекті түрлендіріп жазайық:

n(n²-1)(5n+2)=5n(n²-1)(n+2)-8n(n²-1)= 5(n-1)n * (n+1)(n+2) -8 (n-1)n(n+1). (n-1)n(n+1)(n+2) өрнегі төрт тізбектес натурал санның көбейтіндісі болғандықтан, әрі 3-ке бөлінеді, әрі 8-ге бөлінеді. 8 бен 3 өзара жай сан болғандықтан бұл өрнек 24-ке бөлінеді.

8(n-1)n(n+1) өрнегі де 24-ке бөлінеді, себебі (n-1)n(n+1) көбейтіндісі 3-ке бөлінеді.

Сынып.

№ 1. а мен в сандары х²-6х+1=0 теңдеуінің түбірлері.Кез-келген натурал саны үшін аⁿ+вⁿ өрнегінің бүтін сан болатындығын және 5-ке бөлінбейтіндігін дәлелдеңдер.

Дәлелдеуі:

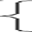Математикалық индукция тәсілін қолданайық. Виет теоремасына сүйеніп жазайық:

ав=1 Сонымен n=1 болғанда аⁿ+вⁿ өрнегі бүтін және 5-ке

а+в=6 бөлінбейді n=k болғанда

а^k+в^k өрнегі бүтін болып 5-ке бөлінбейтін болсын n=k+1 болғанда a^k+1 +в^k+1 өрнегінің бүтін болып және 5-ке бөлінбейтінін дәлелдейік.

(a^k+в^k)(а+в) = a^k+1+ав^k+ ва^k+ в ^k+1= (a^k+1+в^k+1)+ав (в^k-1+ a^k-1)

Осыдан мынадай өрнекке келеміз.

a^k+1+в^k+1=(a^k+в^k)(а+в)- ав (в^k-1+ a^k-1)

Индукция болжамы бойынша a^k+в^kєZ; в^k-1+ a^k-1є z және ав=1, а+в =6. Олай болса, a^k+1 +в^k+1 өрнегі бүтін және 5-ке бөлінбейді. Онда математикалық индукция принципі бойынша аⁿ+вⁿ өрнегінде кез-келген n натурал саны үшін бүтін болады және 5-ке бөлінбейді.

Республикалық олимпиада есептері:

Сынып.

№ 1.(1+√2)¹⁹⁸¹ санының а+ в 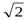түрінде өрнектелетінін дәлелдеңдер, мұндағы a мен в өзара жай сандар

Шешуі: Индукция бойынша дәлелдейміз. Айталық, (1+ 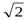)ⁿ=a+в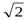

мұндағы а және в – өзара жай сандар. n=1 бұл тура болсын. Сонда (1+ 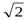)ⁿ⁺¹= (a+в 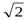) ∙(1+ 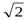)= (a+2в)+(а+в)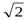

а+2в=а₁ және а+в=в₁ сандары өзара жай, өйткені олай болмаса а=2 в₁- а₁ ,в=а₁-в₁ сандарының да ортақ d>1 бөлгіші бар болар еді. Сонымен, есеп қортындысы кез-келген натурал n үшін тура, демек n=1981 үшін де тура.

№ 2.Екі бала мынандай ойын ойнайды. Бастаушы бірінші жүрісімен берілген n≥2 тастан тұратын үймені өзінің қалауынша 2 немесе 3 үймеге бөледі. Ары қарай кезектесіп жүреді және әрқайсысы өз жүріс кезеңінде кез-келген үймені таңдап алып, өз қалауынша оны 2 немесе 3 үймеге бөледі. Соңғы мүмкін жүрісті жасаған бала ұтады. Дұрыс ойнаса кім ұтады.

Шешуі: Дұрыс ойнаса әрқашанда бастаушы ұтады. Ол үшін ұту стратегиясын көрсетейік. Екі жағдайды қарастырамыз.

1)n- жұп сан. Бірінші жүрісімен бастаушы тастарды тең 2 үймеге бөледі. Сонан соң өз кезегінде қарсыласының жүрісіне симметриялы жүріс жасап отырады.

2)n=2m+1-тақ сан. Бірінші жүрісімен бастаушы тастарының саны m, m және 1 болатын үш үймеге бөледі. Бір тастан тұратын үймені қарастырмасақ та болады. Әры қарай «Симметриялық» әдісті қолданады.

Халықаралық олимпиада есептері:

Сынып.

№ 1. Кез-келген n натурал сан үшін теңдеуді шешіңіздер: cosⁿx-sinⁿx=1

Шешуі: Үш жағдай қарастырамыз:

1) n жұп болсын, яғни n=2m. Онда cos^2mx=1+sin^2mx, cos^2mx≤1≤1+sin^2mx болғандықтан sinx=0 және cosx=±1, яғни x=kπ, kєZ.

2) n- тақ, яғни n=2m+1(m≥1). Онда cos^2m+1x-sin^2m+1x=1. Бұл жағдайда теңдеудің шешімі мынадай түрде жазылады: x=2kπ, не x=2 kπ- ,kєZ

3) n=1. Бұл жағдайда теңдеу cosx-sinx=1 түріндежазылады, немесе cos(x+ 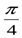)= 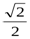. Бұл жағдайдағы шешім екінші жағдайдағымен бірдей болады.

 

 

Теңсіздіктерді дәлелдеу.

 

І. Қарапайым теңсіздіктерді дәлелдеу

Мектеп көлемінде қарапайым теңсіздіктер дәлелденеді, сол теңсіздіктер арқылы күрделі теңсіздіктерде дәлелденеді.

№1 а² + b² ≥ 2ab.

Дәлелдеуі:

a²+ b² - 2аb = (а – b)² ≥ 0.

№2

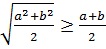кез келген a және b үшін.

Дәлелдеуі:

Берілген теңсіздіктен 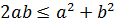, біз мына теңсіздікті аламыз 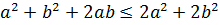бұдан 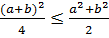немесе 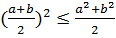соны мына түрде жазамыз 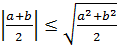бұдан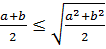

II. Штурм әдісін қолданып теңсіздікті дәлелдеу

Бұл әдісті неміс математигі Р.Штурм ұсынған. Бұл әдістің көмегімен бірнеше теңсіздікті дәлелдейік:

№3 Егер 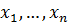қосындысы 1-ге тең болса, онда 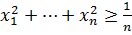дәлелдеу керек

Дәлелдеуі:

Егер 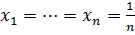онда .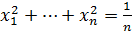

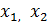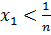
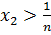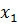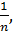
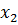Қаралатын сандардың ішінде ең болмағанда екі сан бір-біріне тең болмаса, онда сандардың ішінен екі сан табылады, сонын біреуі - нан үлкен болады, ал екіншісі кіші болады. Осы сандар болсын, және де болсын, онда - ді -ні 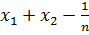- мен алмастырып, мынандай теңсіздік аламыз және олардың қосындысы 1-ге тең.

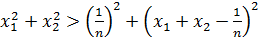болғандықтан, осыдан

.

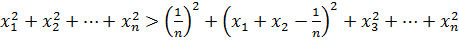Осы амалды бірнеше рет қайталап, шыққан тізбектің кез келген мүшесі -ге тең, ал олардың квадраттарының қосындысы берілген 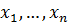сандардың квадраттарының қосындысынан кіші болады.

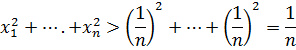
III. Арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолдану әдісі

Кейбір теңсіздіктерді дәлелдегенде, оң a және b сандары үшін арифметикалық, геометриялық, квадраттық, гармониялық орталардың ара қатынасын қолданады: .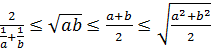

Мына өрнекте 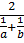гармониялық орта,

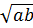– геометриялық орта,

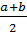– арифметикалық орта,

– квадраттық орта.

Бұл теңсіздікті дәлелдеу әдісі күрделі теңсіздіктерді дәлелдеуде көп қолданылады.

№4 теңсіздікті дәлелде 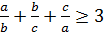, мұндағы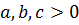

Дәлелдеуі: егер 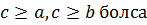, онда 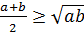- ны қолданып,

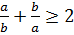-ны (1) аламыз және 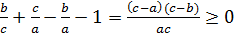осыдан 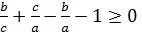(2)

(1) және (2) қосып 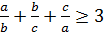аламыз.

IV. Коши-Буняковский әдісін қолдану

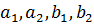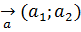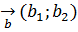Коши-Буняковский әдісін бірінші сандар үшін дәлелдейміз. және векторлары берілсін, мектеп көлемінде белгілі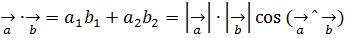

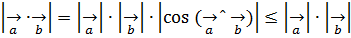
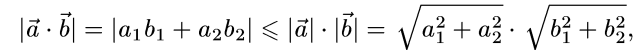
немесе

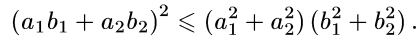
Бұл Коши-Буняковскийдің теңсіздігі 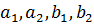сандары үшін орындалатын дербес жағдайы болады.

Коши-Буняковскийдің теңсіздігі 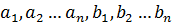сандары үшін келесі жалпы түрде жазылады:

 

№5. Дәлелдеу керек:

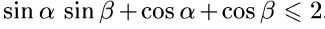
Дәлелдеуі:

 

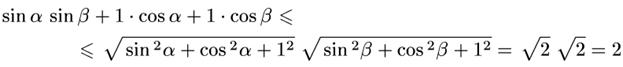
V. Жаңа айнымалы енгізу әдісі

Кейбір теңсіздіктерді дәлелдеу үшін жаңа айнымалы енгізу арқылы мақсатқа жетуге болады.

№6. Теңсіздікті дәлелде

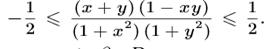
Дәлелдеуі:

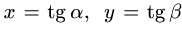
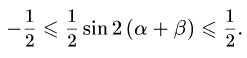
VI. Симметриялық және біртекті қасиеттерді қолдану

№7 Теңсіздікті дәлелде:

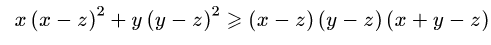
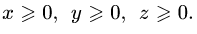
Дәлелдеуі:

Теңсіздікті түрлендіре отырып келесі түрге көшеміз

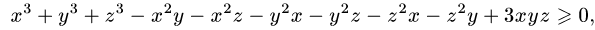
x, y, z айнымалы арқылы симметриялық теңсіздік аламыз, бұдан x y z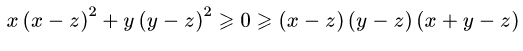

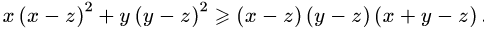
VII. Математикалық индукция тәсілін қолдану

Теңсіздіктерді дәлелдеуде математикалық индукция тәсілін қолдануға болады. Математикалық индукция принциптерін келесі берілген тұжырымдамада барлық натурал n сандары p-дан кіші емес үшін ақиқат, егер:

1) n=p үшін тұжырымдама ақиқат болса,

2) n=k(k p) тұжырымдама ақиқат деп, n=k+1 үшін тұжырымдама ақиқат екенін дәлелдеу керек.

_{№8. Дәлелдеу керек:}

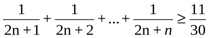_{мұндағы} n>1, n N

Дәлелдеуі:

n=2, 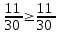_ақиқат

n=k тұжырымдама ақиқат деп алып

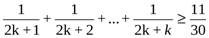
n=k+1 тұжырымдаманың ақиқат екенін дәлелдейміз

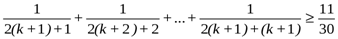
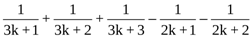
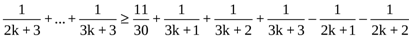
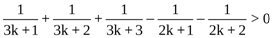
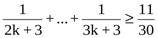
n(n>1)

VIII. Бір теңсіздікті бірнеше рет қолдану тәсілі

_{№9. Қос теңсіздікті дәлелдеу керек:}

,

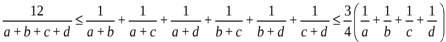a>0, b>0, c>0, d>0.

_{Дәлелдеуі:}

x>0, y>0

_{осы теңсіздікті бірнеше рет қолданып дәлелдейміз}

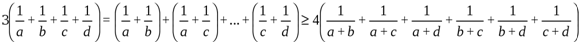
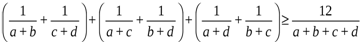
IX. Туынды мен интегралды қолданып дәлелдеу тәсілі

_{Егер функция f(x) және g(x) І аралығында анықталса, және үздіксіз болса, онда,} f(x) _{g(x) теңсіздігін [a,b]=I немесе [a, +∞)=I аралығында дәлелдеу үшін, келесі теореманы қолдануға болады:}

_{Теорема: Егер f(x) және g(x) І аралығында дифференциалданса,}

f(a) _{g(a) осы аралықта және h’(x) 0, мұндағы h(x)= f(x) – g(x), онда}

f(x) _{g(x) теңсіздігі осы аралықта орындалады.}

_{№1. 2}^x+1_{>x+2, x 1 теңсіздікті дәлелде.}

_{Дәлелдеуі: функция h(x)=2}^x+1_{-x-2 [1,+∞) аралығындағы функцияны қарастырамыз.}

_{h(1)=1 және h}^/_(x)=2^x+1_{ln2-1 функциясы y=2}^x _{[1, + ) аралығында өспелі болады, ендеше h}^/_{(x) 4ln2-1>0 бұдан x 1, h(x) h(1) болса немесе}

₂^x+1 _x+3,

₂^x+1_{>x+2 онда орындалады.}

 

 

_{Мектепішілік олимпиада}

_{№ 1.Теңсіздікті дәлелдеңдер.}

_(a+в+c)( + + )≥9 (мұндағы а>0, в>0,с>0)

Теңсіздіктің сол бөлігін түрлендірейік:

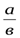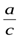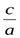_(a+в+c)( + + )=1+ + +1+ + + + +1=3( + )+( + )+( + )≥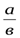

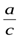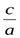≥3+2+2+2=9 (себебі әр жақшаның ішіндегі қосынды 2-ге тең немесе одан үлкен).

№ 2.

≥а₁а₂ а₃ а₄ (мұндағы а₁ >0,а₂>0,а₃>0,а₄ >0)

Нұсқау.Екі оң санның арифметикалық орташасы мен геометриялық орташасын екі рет салыстыруды қолданамыз.

№ 3. Егер а²+в² =1 болса, │ а+в │≤ 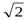онда екенін дәлелдеңіздер.

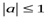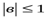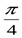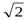және екені есептің шартынан шығады. Сондай –ақ а²+в² =1 болғандықтан, а мен в- ны синуспен және косинуспен ауыстыруға болады: a=sinα, в=cosα. Онда а+в=sinα+cosα=sinα+sin = =2sin cos = cos .

cos ≤1.Демек, │а+в│≤ .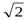

Басқашаталқылапкөрелік: 1=а²+в²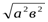≥2 =2 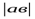; 2≥а²+в²+2 = ;

≥ .

 

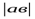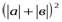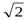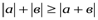Аудандықолимпиада

Сынып

№ 1.Теңсіздіктішеш:

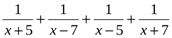> 0

Теңсіздіктіңсолжағынортақбөлімгекелтіріпықшамдапжазайық.

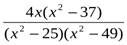>0

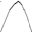
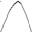
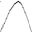
С ондаберілгентеңсіздіккемәндестеңсіздік 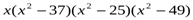>0 болады.

- + - + - + - +

-7 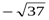-5 0 5 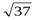7

.

 

 

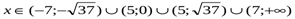№ 2. Теріс емес, а,в,с сандары үшін теңсіздікті дәлелдеңдер: (а+в)(в+с)(с+а)≤8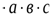

Нұсқау: Мынадай үш теңсіздікті көбейту керек .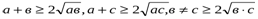

Сынып.

№ 1. х -кез-келген сан болсын, дәлелдеңдер: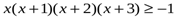

Дәлелдеуі: x(x+3)(x+1)(x+2)=(x²+3x)(x²+3x+2)=((x²+3x+1)-1)((x²+3x+1)+1)=(x²+3x+1)²-1≥-1

 

Облыстық олимпиада

Сынып

№ 1.Теңсіздікті дәлелдеңдер.

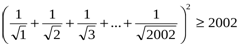
Шешуі:

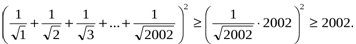
Сынып

№ 2.Теңсіздікті дәлелдеңдер.

>

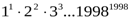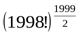
Дәлелдеуі: Теңсіздікті К≤999 натурал сандар үшін дәлелдейік:

>

>

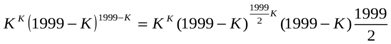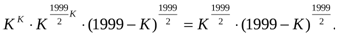
Сондықтан, > ;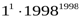

> ... >

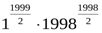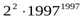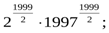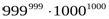
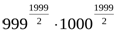
Бұл теңсіздіктерді мүшелеп көбейтіп, дәлелденілген теңсіздікке келеміз.

Сынып

№ 1. a>в>0 сандары үшін > теңсіздігін дәлелдеңдер.

Дәлелдеуі: Дәлелденетін теңсіздік мынадай теңсіздікпен мәндес:

<

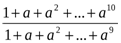
немесе <

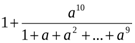
немесе <

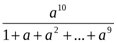
немесе >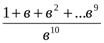

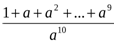
немесе >

Соңғы теңсіздік тура болғандықтан дәлелденілетін теңсіздік те тура болады.

Республикалық олимпиада

Сынып

№ 1.а+в+с=1, (a,в,с≥0) шарттарын қанағаттандыратын а,в,с сандары үшін теңсіздікті дәлелдеңіздер. (1+а)(1+в)(1+с)≥8(1-а)(1-в)(1-с).

Дәлелдеуі: 1+а=(1-в)+(1-с) онда 1+ 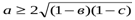. Осы сияқты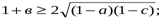 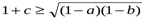.Бұл теңсіздіктерді мүшелеп көбейтсек, дәлелденілетін теңсіздік шығады.

Сынып

№ 1. Оң x,y,z сандары үшін теңсіздікті дәлелдеңдер:

x(1+y)+y(1+z)+z(1+x)≥6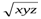

Дәлелдеуі:Белгілі а+в≥2 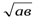теңсіздігін (а,в, ≥0) пайдаланып x+yz≥2 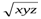, y+xz≥2 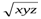, z+xy≥2 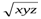теңсіздіктерін аламыз. Осы үш теңсіздікті қосып

x+yz+y+xz+z+xy=x(1+y)+y(1+z)+z(1+x)>6 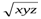теңсіздігін аламыз.

Сынып.

№ 1. Теріс емес а,в үшін 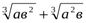≤а+в теңсіздігін дәлелдеңдер.

Бізге 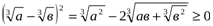теңсіздігінен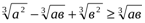

шығатыны анық.Соңғы теңсіздіктің екі жағын 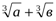-қа көбейтсек, бізге керекті теңсіздік шыға келеді.

 

 

Халықаралық олимпиада

№ 1. а,в,с оң сандар болып және авс=1. Мынадай теңсіздікті дәлелдеңіздер:

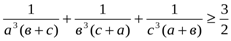
Дәлелдеуі: Жаңа белгілер енгізейік: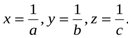

Есептің шарты бойынша xyz=1. Енді дәлелденілетін теңсіздік мынадай теңсіздікпен мәндес болады.

S= 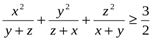(1)

Біз оң сандардың арифметикалық ортасы мен геометриялық ортасының арасындағы байланысты қолданамыз: 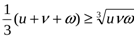(2)

Енді Коши-Буняковский теңсіздігін қолданамыз:

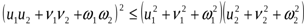
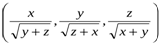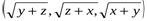бұл теңсіздікті және векторларына қолданып жазамыз: 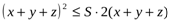немесе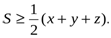

Енді 2) теңсіздікті қолданып табамыз

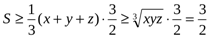
№ 2. Ауданы S келетін үшбұрыштың қабырғалары а,в,с болсын. Мынадай теңсіздікті дәлелдеңіздер: а²+в²+с²≥4S 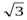. Теңдік қашан болады?

Дәлелдеуі: Герон формуласын жазайық.

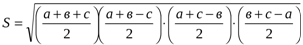
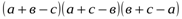көбейтіндісын бағалау үшін мынадай теңсіздікті қолданайық 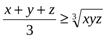немесе xyz 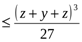. Белгілеулер енгізейік: 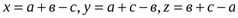. Енді мынадай теңсіздіктерді жазуға болады:

 

 

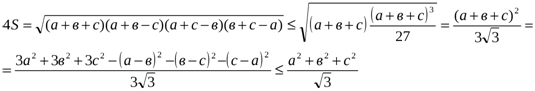
теңдік а=в=с болғанда орындалады.

Қорытындылай келе, қазіргі уақытта білім беру қызметкерлерінің алдында тұрған басты мақсат- еліміздегі білім беруді халықаралық деңгейге көтеру және білім сапасын көтеру, жеке тұлғаны қалыптастыру, қоғам қажеттілігін өтеу, оны әлемдік білім кеңістігіне кіріктіру болмақ. Сондықтан, математика пәнінен деңгейі жоғары оқушылармен олимпиадалық есептерді дайындық ретінде қарастыруға болады деп ойлаймын.

 

 

Пайдаланылған әдебиеттер.

 

1.Алгебра оқулығы 9-кл. А.Е. Әбілқасымова, Н.Р.Майкотов, Қ.И.Қаңлыбаев.

2. Т.Т.Абылайханов, Т.Т. Абылайханов «Математика есептері»

3. «Математика в школе» №3; 1991

4.Информатика, физика, математика №6; 1998

5.Информатика, физика, математика №3; 2001

6.Математика,физика №2; 2003