Рассмотрение стационарных задач квантовой механики начнем с наиболее простой для анализа задачи - о движении частицы в потенциальной яме с непроницаемыми, т.е. бесконечно высокими стенками. Такие ямы называют еще потенциальными ящиками, наиболее часто это название применяется по отношению к трехмерной потенциальной яме. Выявленные при этом особенности движения, такие, например, как квантование энергии, вырождение энергетических уровней и т.д. в дальнейшем будут проанализированы для случая ямы конечной глубины.
Одномерная потенциальная яма. Рассмотрим частицу, находящуюся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. В этом случае потенциальная энергия частицы  имеет вид
имеет вид


т.е. внутри ямы ( ) потенциальная энергия
) потенциальная энергия  постоянна и равна нулю, а вне ямы обращается в бесконечность (рис.4.1).
постоянна и равна нулю, а вне ямы обращается в бесконечность (рис.4.1).
 |
| Рис. 4.1. |
Запишем уравнение Шредингера для одномерного движения частицы вдоль оси 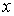
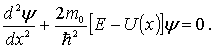 | (4.11) |
Поскольку вне ямы потенциальная энергия обращается в бесконечность, то для того, чтобы выполнялось уравнение (4.11), необходимо, чтобы вне ямы волновая функция  обращалась в ноль, т.е.
обращалась в ноль, т.е.  . Это означает, что в случае ямы с бесконечно высокими стенками частица не может выйти за пределы ямы, поскольку такие стенки являются непроницаемыми для частицы. В силу непрерывности волновая функция
. Это означает, что в случае ямы с бесконечно высокими стенками частица не может выйти за пределы ямы, поскольку такие стенки являются непроницаемыми для частицы. В силу непрерывности волновая функция  должна обращаться в нуль и на границах ямы: при
должна обращаться в нуль и на границах ямы: при  и при
и при 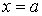 .
.
Таким образом, задача о движении частицы в яме сводится к решению уравнения
 | (4.12) |
с граничными условиями

Введем обозначение
 | (4.13) |
При этом уравнение (4.12) принимает вид хорошо известного из теории колебаний уравнения

решение которого есть
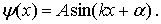 | (4.14) |
Используя граничное условие  , получаем
, получаем

откуда следует, что  , где
, где 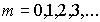 . Отметим, что при четных значениях
. Отметим, что при четных значениях  и при
и при 
 , а при нечетных значениях
, а при нечетных значениях 
 . Однако, физический смысл имеет не сама волновая функция
. Однако, физический смысл имеет не сама волновая функция  , а квадрат ее модуля
, а квадрат ее модуля  , который от выбора значения
, который от выбора значения  , т.е. от знака
, т.е. от знака  не зависит. Поэтому без потери общности можно считать, что
не зависит. Поэтому без потери общности можно считать, что  .
.
Второе граничное условие  приводит к соотношению
приводит к соотношению
которое для  выполняется при
выполняется при
 | (4.15) |
Отметим, что значение  , формально также входящее в решение (4.14), не удовлетворяет условию задачи, т.к. при этом
, формально также входящее в решение (4.14), не удовлетворяет условию задачи, т.к. при этом 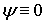 , что означает, что частица в яме отсутствует. Поэтому значение
, что означает, что частица в яме отсутствует. Поэтому значение  следует отбросить.
следует отбросить.
Подставляя (4.13) в (4.15), приходим к выражению для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками
 | (4.16) |
Важной особенностью полученного энергетического спектра (4.16) является его дискретность. Частица, находящаяся в потенциальной яме, может иметь только дискретные, квантованные, значения энергии, определяемые выражением (4.16) (см.рис.4.2). Отметим, что решение
 |
| Рис. 4.2. |
уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.
Число  в (4.16), определяющее энергию частицы в яме, называется квантовым числом, а соответствующее ему значение
в (4.16), определяющее энергию частицы в яме, называется квантовым числом, а соответствующее ему значение  - уровнем энергии. Состояние частицы с наименьшей энергией, в данном случае с
- уровнем энергии. Состояние частицы с наименьшей энергией, в данном случае с  , называется основным состоянием. Все остальные состояния являются возбужденными: значение
, называется основным состоянием. Все остальные состояния являются возбужденными: значение  отвечает первому возбужденному состоянию, значение
отвечает первому возбужденному состоянию, значение  - второму возбужденному состоянию и т.д.
- второму возбужденному состоянию и т.д.
Следует отметить, что минимальное значение энергии частицы, находящейся в основном состоянии, отлично от нуля. Этот результат согласуется с соотношением неопределенностей и является общим для всех задач квантовой механики. В классической механике минимальную энергию, равную нулю, имеет покоящаяся в яме частица. Такого состояния покоя у квантовой частицы не существует.
Обсудим подробнее вопрос о дискретности энергетического спектра. Разность энергий  -го и
-го и  -го энергетических уровней
-го энергетических уровней 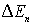 равна
равна

Оценим величину  для конкретных случаев.
для конкретных случаев.
Случай 1. Рассмотрим молекулу газа массой  кг в сосуде размером
кг в сосуде размером  м. При этом
м. При этом

Энергетическое расстояние между соседними уровнями оказывается столь малым по сравнению с энергией теплового хаотического движения молекулы  (при комнатной температуре
(при комнатной температуре  эВ), что практически можно говорить о сплошном энергетическом спектре движущейся молекулы.
эВ), что практически можно говорить о сплошном энергетическом спектре движущейся молекулы.
Случай 2. Рассмотрим свободный электрон ( кг) в металле
кг) в металле
( м). В этом случае
м). В этом случае

т.е. энергетическое расстояние между уровнями много меньше характерного значения энергии электронов в металле, составляющего по порядку величины ~ 1 эВ. Однако, как будет показано в главе VI, наличие дискретных уровней даже в случае потенциальной ямы макроскопических размеров для электронов имеет принципиально важное значение. 
Случай 3. Рассмотрим свободный электрон в атоме ( м). При этом разность энергий соседних уровней равна
м). При этом разность энергий соседних уровней равна

Это заметная величина по сравнению, например, с энергией связи электрона в атоме (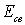 ~ 10 эВ). Поэтому дискретность энергетического спектра в этом случае оказывается весьма существенной.
~ 10 эВ). Поэтому дискретность энергетического спектра в этом случае оказывается весьма существенной.
Завершая обсуждение энергетического спектра частицы в потенциальной яме (4.16), отметим еще одно его свойство. Рассмотрим отношение  к
к 

При увеличении квантового числа  это отношение уменьшается
это отношение уменьшается  , таким образом, дискретность энергетического спектра с возрастанием
, таким образом, дискретность энергетического спектра с возрастанием  играет все меньшую роль. Данный результат представляет собой проявление важного физического принципа - принципа соответствия, согласно которому при больших значениях квантового числа
играет все меньшую роль. Данный результат представляет собой проявление важного физического принципа - принципа соответствия, согласно которому при больших значениях квантового числа  , т.е. при
, т.е. при 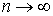 , квантовая механика переходит в механику классическую.
, квантовая механика переходит в механику классическую.
Волновые функции частицы в одномерной яме. Перейдем теперь к анализу волновых функций частицы, находящейся в одномерной потенциальной яме. Из (4.14) с учетом (4.15) получаем

Множитель 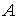 находится из условия нормировки волновой функции (4.10)
находится из условия нормировки волновой функции (4.10)
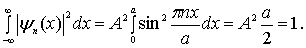
Таким образом, для 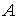 получаем
получаем

и волновые функции частицы в одномерной потенциальной яме с бесконечно высокими стенками имеют вид
 | (4.17) |
Отметим, что эти функции, в согласии с общей теорией (см. 3.5), являются ортонормированными, т.е.

где  - символ Кронекера
- символ Кронекера
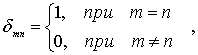 | (4.18) |
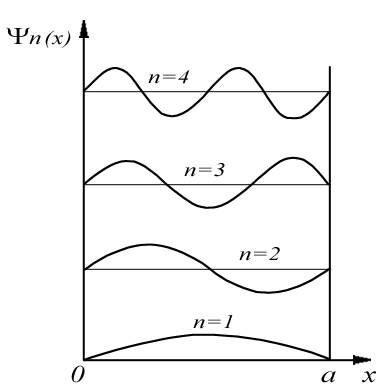
Графики волновых функций  для первых четырех значений квантового числа
для первых четырех значений квантового числа  приведены на рис.4.3. Волновые функции, отвечающие
приведены на рис.4.3. Волновые функции, отвечающие
 |
| Рис. 4.3. |
разным значениям  , существенно отличаются друг от друга. Если поместить начало координат в середину ямы, то волновые функции частицы внутри ямы для нечетных значений
, существенно отличаются друг от друга. Если поместить начало координат в середину ямы, то волновые функции частицы внутри ямы для нечетных значений  будут четными функциями координаты
будут четными функциями координаты 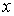 , и наоборот, волновые функции для четных
, и наоборот, волновые функции для четных  - нечетными функциями координаты. При увеличении квантового числа
- нечетными функциями координаты. При увеличении квантового числа  на единицу число точек пересечения волновой функции с осью
на единицу число точек пересечения волновой функции с осью 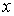 также увеличивается на единицу.
также увеличивается на единицу.
Отличительным свойством найденных волновых функций является излом, т.е. скачок производной на границах ямы. Этот скачок возникает вследствие того, что на границах ямы потенциальная энергия частицы  обращается в бесконечность. В случае ямы конечной глубины, как показано в разделе 4.4, скачок производной волновой функции на границе ямы отсутствует, т.е. волновая функция является гладкой.
обращается в бесконечность. В случае ямы конечной глубины, как показано в разделе 4.4, скачок производной волновой функции на границе ямы отсутствует, т.е. волновая функция является гладкой.
На рис.4.4 представлены графики квадрата модуля волновой функции  , определяющего плотность вероятности нахождения частицы в яме.
, определяющего плотность вероятности нахождения частицы в яме.
 |
| Рис. 4.4. |
Плотность вероятности оказывается существенно различной для разных состояний частицы, т.е. для разных значений квантового числа  . Так, например, в основном состоянии, т.е. при
. Так, например, в основном состоянии, т.е. при  , частица с наибольшей вероятностью находится в центре ямы, а в первом возбужденном состоянии, т.е. при
, частица с наибольшей вероятностью находится в центре ямы, а в первом возбужденном состоянии, т.е. при  , вероятность обнаружить частицу в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно. Такое поведение кардинально отличается от поведения в яме классической частицы, для которой плотность вероятности нахождения частицы одинакова в любой точке ямы.
, вероятность обнаружить частицу в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно. Такое поведение кардинально отличается от поведения в яме классической частицы, для которой плотность вероятности нахождения частицы одинакова в любой точке ямы.
Вероятность того, что частица в яме находится в области  , определяется выражением
, определяется выражением
 | (4.19) |
Отметим, что с математической точки зрения задача о движении частицы в одномерной потенциальной яме с непроницаемыми стенками аналогична задаче о колебании струны с закрепленными концами. И в том, и в другом случае из граничных условий следует, что на ширине ямы (на длине струны) должно укладываться целое число полуволн  . В нашем случае
. В нашем случае  - это дебройлевская длина волны частицы в яме
- это дебройлевская длина волны частицы в яме  .
.
Двумерная потенциальная яма. Рассмотрим частицу, находящуюся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками. В этом случае потенциальная энергия частицы  имеет вид
имеет вид
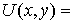

где  - прямоугольная область на плоскости
- прямоугольная область на плоскости  (рис.4.5). Вне потенциальной ямы, как и в одномерном случае,
(рис.4.5). Вне потенциальной ямы, как и в одномерном случае,
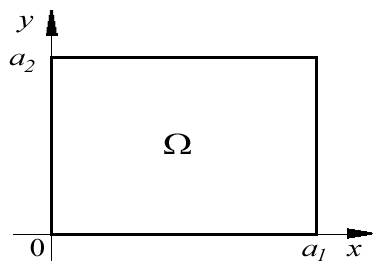 |
| Рис. 4.5. |
волновая функция частицы 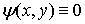 . Поскольку движение частицы в яме вдоль осей
. Поскольку движение частицы в яме вдоль осей 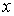 и
и  происходит независимо, то волновую функцию
происходит независимо, то волновую функцию  будем искать в виде произведения
будем искать в виде произведения
 | (4.20) |
где  - функция, зависящая только от координаты
- функция, зависящая только от координаты 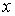 , а
, а  - функция, зависящая только от координаты
- функция, зависящая только от координаты  . Подставляя волновую функцию (4.20) в уравнение Шредингера (4.6), получаем
. Подставляя волновую функцию (4.20) в уравнение Шредингера (4.6), получаем
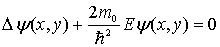
или

Разделив левую и правую части этого выражения на 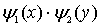 , приходим к соотношению
, приходим к соотношению
 | (4.21) |
Первое слагаемое в левой части (4.21) зависит только от 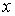 , а второе - только от
, а второе - только от  . Поскольку их сумма равна постоянной величине, то это означает, что каждое из слагаемых также представляет собой постоянную величину, т.е.
. Поскольку их сумма равна постоянной величине, то это означает, что каждое из слагаемых также представляет собой постоянную величину, т.е.

где 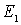 и
и 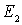 - константы, имеющие размерность энергии, причем
- константы, имеющие размерность энергии, причем  . Таким образом, уравнение Шредингера для двумерной задачи разделяется на два одномерных уравнения
. Таким образом, уравнение Шредингера для двумерной задачи разделяется на два одномерных уравнения
 | (4.22) |
решения которых были нами получены в предыдущем параграфе. Функции
 и
и  имеют вид
имеют вид

где квантовые числа  и
и  принимают значения
принимают значения 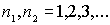 . В результате волновая функция частицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками, есть
. В результате волновая функция частицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками, есть
 | (4.23) |
Энергия частицы в двумерной яме определяется выражением
 | (4.24) |
Энергетический спектр частицы (4.24), как и следовало ожидать, является дискретным и зависит от двух квантовых чисел 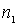 и
и  .
.
Рассмотрим движение частицы в квадратной потенциальной яме, т.е. при  . В этом случае энергетический спектр частицы имеет вид
. В этом случае энергетический спектр частицы имеет вид
 | (4.25) |
Из (4.25) следует, что одному и тому же энергетическому уровню  , определяемому квантовыми числами
, определяемому квантовыми числами  и
и  , при
, при  соответствуют два различных состояния частицы, описываемых волновыми функциями
соответствуют два различных состояния частицы, описываемых волновыми функциями  и
и  . Энергетический уровень, которому соответствует не одно, а несколько состояний частицы, называется вырожденным уровнем, а число соответствующих ему состояний называется кратностью вырождения или степенью вырождения уровня. В случае двумерной квадратной потенциальной ямы кратность вырождения энергетического уровня, для которого
. Энергетический уровень, которому соответствует не одно, а несколько состояний частицы, называется вырожденным уровнем, а число соответствующих ему состояний называется кратностью вырождения или степенью вырождения уровня. В случае двумерной квадратной потенциальной ямы кратность вырождения энергетического уровня, для которого  , равна двум. Энергетический уровень, которому соответствует одно состояние частицы, называется невырожденным. В двумерной квадратной потенциальной яме невырожденными являются энергетические уровни с
, равна двум. Энергетический уровень, которому соответствует одно состояние частицы, называется невырожденным. В двумерной квадратной потенциальной яме невырожденными являются энергетические уровни с  .
.
Трехмерная потенциальная яма. Рассмотрим частицу, находящуюся в трехмерной потенциальной яме с бесконечно высокими стенками (потенциальном ящике). Обозначим через  внутреннюю область прямоугольного параллелепипеда (рис.4.6). В данной задаче потенциальная энергия частицы
внутреннюю область прямоугольного параллелепипеда (рис.4.6). В данной задаче потенциальная энергия частицы  имеет вид
имеет вид
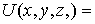

Вне потенциальной ямы волновая функция частицы  . Внутри
. Внутри
 |
| Рис. 4.6. |
ямы будем, так же как и в двумерном случае, искать волновую функцию в виде произведения

где функция  зависит только от координаты
зависит только от координаты 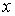 ,
,  - зависит только от
- зависит только от  ,
,  - только от
- только от  .
.
Используя тот же самый метод решения, что и для двумерной ямы, из уравнения Шредингера в трехмерном случае получаем три одномерных уравнения

где 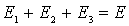 . Решение этих уравнений, обращающееся в нуль на границе области
. Решение этих уравнений, обращающееся в нуль на границе области  , т.е. на непроницаемых стенках потенциального ящика, определяет вид волновой функции частицы
, т.е. на непроницаемых стенках потенциального ящика, определяет вид волновой функции частицы
 | (4.26) |
 | (4.27) |
Здесь квантовые числа  ,
,  и
и  принимают значения
принимают значения  . Отметим, что и волновая функция частицы, и ее энергия в случае трехмерной потенциальной ямы зависят от трех квантовых чисел.
. Отметим, что и волновая функция частицы, и ее энергия в случае трехмерной потенциальной ямы зависят от трех квантовых чисел.
Рассмотрим движение частицы в кубической потенциальной яме, т.е. будем считать, что  . В этом случае энергетический спектр частицы имеет вид
. В этом случае энергетический спектр частицы имеет вид
 | (4.28) |
Энергетические уровни в кубической яме, для которых  , являются невырожденными, все остальные уровни вырождены. Вопрос о кратности вырождения энергетических уровней в кубической яме рассмотрен в задаче 4.4.
, являются невырожденными, все остальные уровни вырождены. Вопрос о кратности вырождения энергетических уровней в кубической яме рассмотрен в задаче 4.4.
 2018-02-14
2018-02-14 2411
2411







