Напряженность электрического поля – это физическая величина, равная силе, действующей на положительный единичный точечный заряд, помещенный в данную точку поля

 

                                                  (3)

 

Из определения напряженности следует, что сила, действующая со стороны электрического поля на точечный заряд, равна:

 

                                                 (4)

 

Единица напряженности электрического поля в системе СИ - .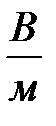

 

Исходя из закона Кулона (1) и определения (3), можно легко рассчитать напряженность электрического поля, создаваемого одиночным точечным зарядом в вакууме:

 

                                          (5)

 

теорема Гаусса – важнейшая теорема электростатики: поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность, содержащую электрические заряды, равен отношению алгебраической суммы этих зарядов к электрической постоянной и диэлектрической проницаемости среды, которой заполнено пространство внутри поверхности.

 

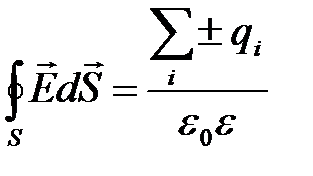                                                                                                                  (6)

 

Согласно известному из курса механики принципу независимости действия сил, результирующее значение напряженности поля, создаваемого одновременно несколькими электрическими зарядами в одной и той же точке пространства, определяется согласно принципу суперпозиции: результирующая напряженность электрического поля равна векторной сумме напряженностей полей, создаваемых каждым из имеющихся зарядов:

 

                                                                                                                             (7)

 

Электрическое поле характеризуется также потенциалом - энергетической величиной, равной потенциальной энергии положительного единичного точечного заряда, помещенного в данную точку поля:

 

                                                 (8)

где  - потенциал,  - потенциальная энергия взаимодействия электрического заряда с полем, 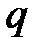 - величина этого заряда. Размерность потенциала в системе СИ: .

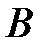Потенциал точечного заряда в вакууме равен

 

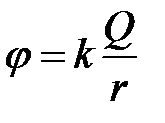                                                             (9)

 

Результирующее значение потенциала, создаваемого одновременно несколькими электрическими зарядами в одной и той же точке пространства, определяется согласно принципу суперпозиции: результирующий потенциал электрического поля равен алгебраической сумме потенциалов полей, создаваемых каждым из имеющихся зарядов:

 

                                                                                                                     (10)

 

Отметим, что потенциал - скалярная величина, которая определяется с точностью до произвольной постоянной. Разность потенциалов связана с работой сил электрического поля по перемещению точечного заряда следующим образом:

 

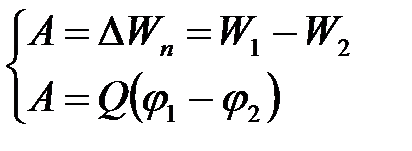                             (11)

 

где  - потенциалы начальной и конечной точек положения заряда. Вспомним, что введение понятий потенциала и потенциальной энергии заряда в электрическом поле связано с тем, что работа по перемещению заряда в электрическом поле не зависит от траектории перемещения, а определяется лишь началь­ным и конечным положением заряда. В соответствие с (11) эта ра­бота определяется разностью потенциалов начальной и конечной точек.

Напряженность и потенциал - два параметра электростати­ческого поля. Для нахождения связи между ними рассчитаем работу при малом перемещении точечного заряда в электрическом по­ле из точки 0 в точку А (рисунок 1).

 

Элементарная механическая работа при таком перемещении вычисляется так:

 

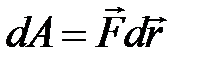                                                          (12)

 

В соответствие с формулой (11) эта же работа равна:

 

                                           (13)

 

Сопоставляя формулы (13) и (12) и учитывая явное выражение для силы (4), получим

 

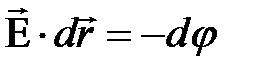                                                     (14)

 

Переместим теперь заряд из точки  в точку 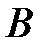 на расстояние  при фиксированных значениях координат  и 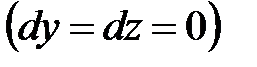. В соответствии с формулой (13) получим:

 

                                        (15)

 

где  - проекция вектора напряженности на ось . Последнюю фор­мулу перепишем так:       

 

                                                      (16)

 

где частная производная находится путем дифференцирования по­тенциала по координате  при фиксированных значениях  и . По аналогии можно получить выражения для проекции вектора напряженности на другие оси координат:

 

                                          (17)

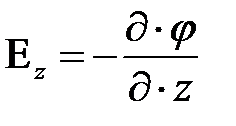                                                       (18)

 

Из полученных проекций легко "сконструировать" вектор напряжен­ности электрического поля

 

                   (19)

 

Выражение в скобках называется градиентом потенциала и сокра­щенно записывается так:

 

 или                            (20)

 

Градиент функции - это вектор, характеризующий скорость пространственного изменения функции и направленный в сторону максимального её возрастания. Как видно из формулы (20), вектор напряженности электрического поля направлен в сторону, противоположную максимальному возрастанию потенциала.

Отметим, что во многих практических задачах требуется зна­ние напряженности электрического поля. Однако легче рассчитать скалярную величину - потенциал, а затем по формуле (20) вычислить вектор напряженности электрического поля.

 

 

Формула (19) упрощается, если электрическое поле однородно, обладает аксиальной или центральной симметрией:

 

                                                         (21)

 

где  показывает направление изменения электрического поля.

Силовая линия электростатического поля – это геометрическая кривая, в каждой точке которой вектор напряженности электрического поля направлен к ней по касательной.

 

Эквипотенциальные поверхности – это поверхности, во всех точках которых потенциал имеет одно и то же значение.

Такая работа равна нулю, поскольку определяется разностью потен­циалов точек 1 и 2. С другой стороны, работа записывается так:

 

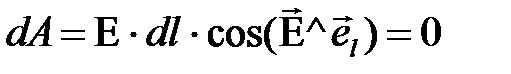                      (22)

 

где  - единичный вектор, направленный по касательной к экви­потенциальной поверхности. Из формулы (22) следует, что косинус угла между векторами  и 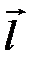 равен нулю и вектор  перпендику­лярен эквипотенциальной поверхности. Далее, переместимся по нормали  к эквипотенциальной пове­рхности в сторону уменьшения потенциала. В этом случае  и из формулы (21) следует, что . Значит, вектор  направлен по нормали в сторону уменьшения потенциала.