Вычисление площади поверхности вращения
Пусть кривая АВ является графиком функции у = f (x)≥0, где x 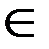 [ a; b ], f ʹ (x)
[ a; b ], f ʹ (x) 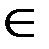 С[ a; b ].
С[ a; b ].
Требуется найти площадь S поверхности вращения кривой АВ вокруг оси Оx.
Вычисление площади на основе метода дифференциалов.
1. Через точку x 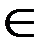 [ a; b ] проводим плоскость Π1 (Π1
[ a; b ] проводим плоскость Π1 (Π1 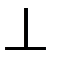 Ох). Пересечение тела плоскостью – окружность радиусом у = f (x).
Ох). Пересечение тела плоскостью – окружность радиусом у = f (x).
2. Часть поверхности, лежащей слева от Π1 является функцией от x:
s = s (x) (s (a)=0, s (b)= S).
3. Дадим аргументу x приращение
∆ x = dx, x +∆ x 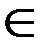 [ a; b ].
[ a; b ].
Через точку x +∆ x проводим плоскость Π2 (Π2 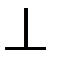 Ох). Функция s (x) получает приращение ∆ s.
Ох). Функция s (x) получает приращение ∆ s.
4. Находим дифференциал площади ds, заменяя образованную между Π1 и Π2 фигуру усеченным конусом, образующая которого равна dl, а радиусы оснований – у и у + dу.
Площадь боковой поверхности равна
ds = π(у + у + dу) dl = 2π уdl + π dуdl,
где dуdl – бесконечно малая высшего порядка, чем ds.
Тогда
ds = 2π уdl = 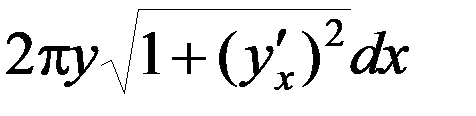 ,
,
(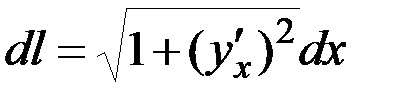 - длина дуги).
- длина дуги).
5. Площадь поверхности вращения:
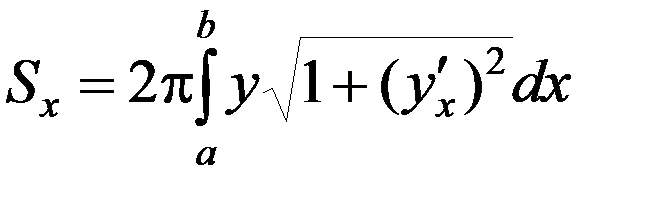 . (1)
. (1)
Пусть кривая АВ задана параметрически
|
|
|
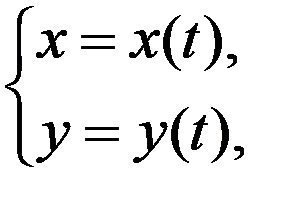 t
t  [α;β],
[α;β],
где x (t), y (t)  С[α;β], xʹ (t), yʹ (t)
С[α;β], xʹ (t), yʹ (t) 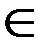 С[α;β]; x (α)= a, y (β)= b.
С[α;β]; x (α)= a, y (β)= b.
В этом случае
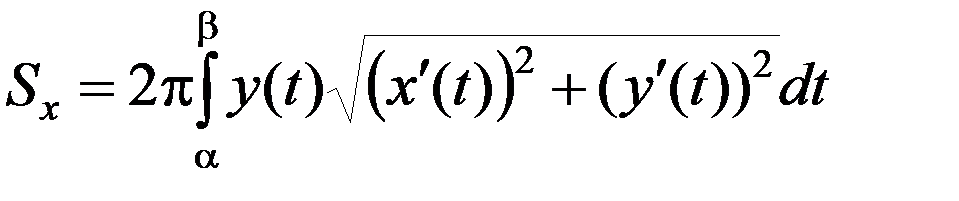 . (2)
. (2)
Пример 8. Найти площадь поверхности шара радиуса R.
Решение ▼ Поверхность шара образована вращением полуокружности
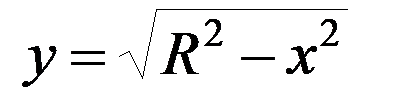 , x
, x 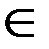 [– R; R ]
[– R; R ]
вокруг оси Ох.
По формуле (1)
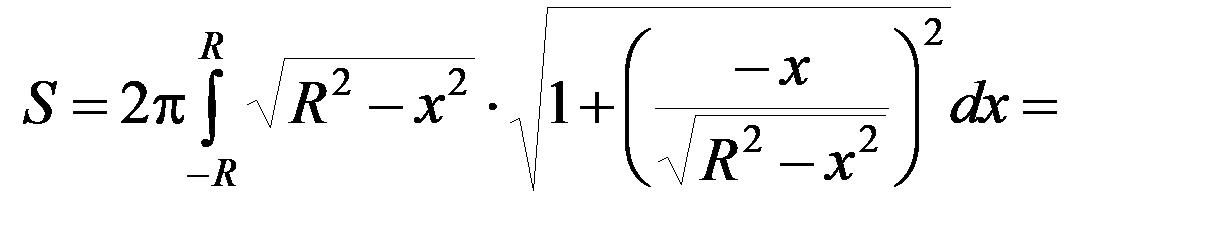
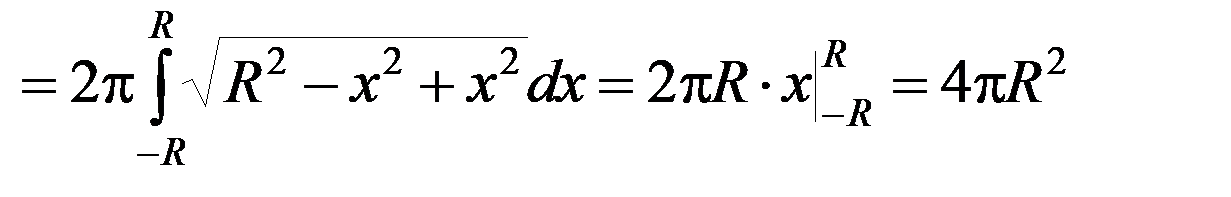 .
.
▲
На основе определенного интеграла находятся:
- работа переменной силы;
- путь, пройденный телом;
-давление жидкости на вертикальную пластину;
-координаты центра тяжести плоской фигуры.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Формула трапеций
Пусть f (x) 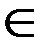 С[ a; b ]. Требуется вычислить определенный интеграл
С[ a; b ]. Требуется вычислить определенный интеграл
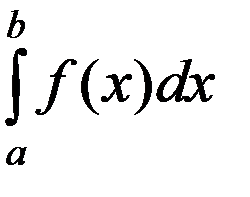 ,
,
численно равный площади соответствующей криволинейной трапеции.
1. Отрезок [ a; b ] разбиваем на n равных частей длиной
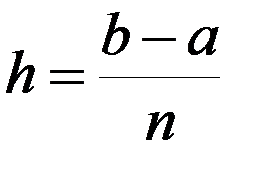 .
.
Абсциссы точек деления a = x 0, x 1, x 2,…, xn = b:
xi = a + hi.
Значения функции в точках деления: y 0 = f (a), y 1 = f (x 1),
y 2 = f (x 2), …, yn = f (b).
2. Кривую y = f (x) заменяем ломаной линией, звенья которой соединяют концы ординат yi и yi +1,  .
.
3. Площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями yi, yi +1 и высотой h:
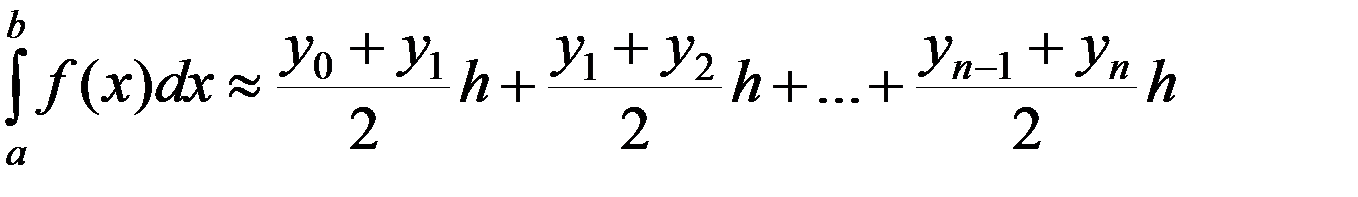
или
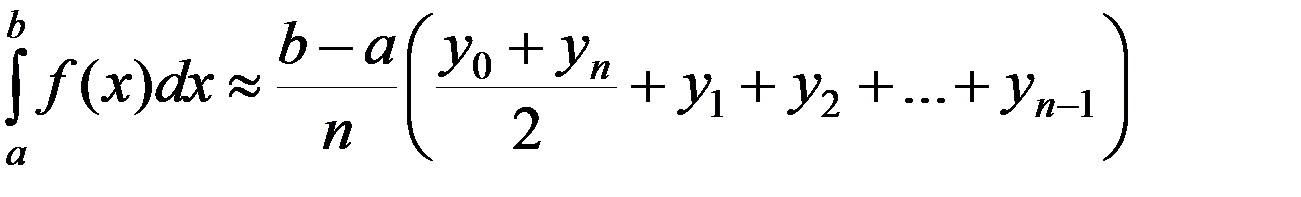 . (1)
. (1)
Выражение (1) называется формулой трапеций.
Пусть
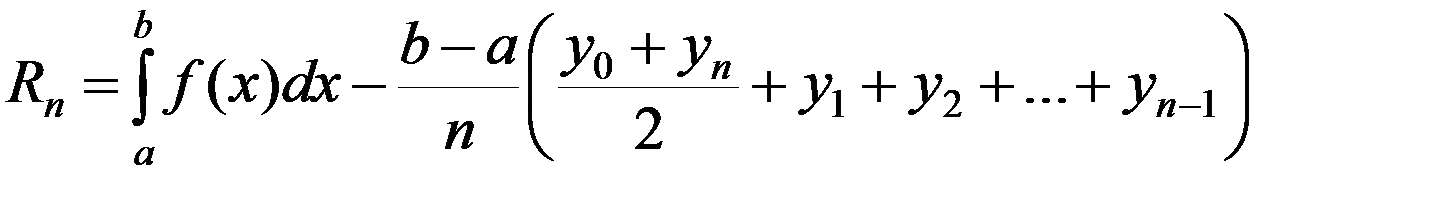 -
-
- абсолютная погрешность приближения по формуле (1).
Известно, что
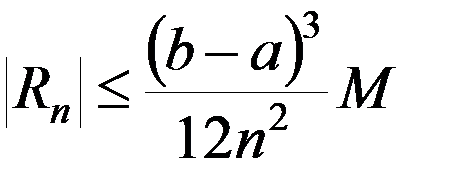 ,
,
где 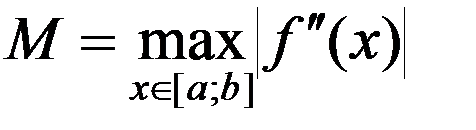 .
.
Для линейной функции y = kx + b абсолютная погрешность Rn =0.
Формула парабол (Симпсона)
Если график функции y = f (x) заменить дугами парабол между точками yi –1, yi, yi +1, то получится более точная формула вычисления интеграла.
|
|
|
1. Найдем площадь криволинейной трапеции, ограниченной сверху параболой
y = ax 2 + bx + c,
сбоку – прямыми x = – h, x = h, снизу – отрезком [– h; h ].
Пусть парабола проходит через три точки
М1(– h; у 0), М2(0; у 1), М3(h; у 2),
где у 0= ah 2 – bh + c, у 1= c, у 2= ah 2 + bh + c. (2)
Площадь равна
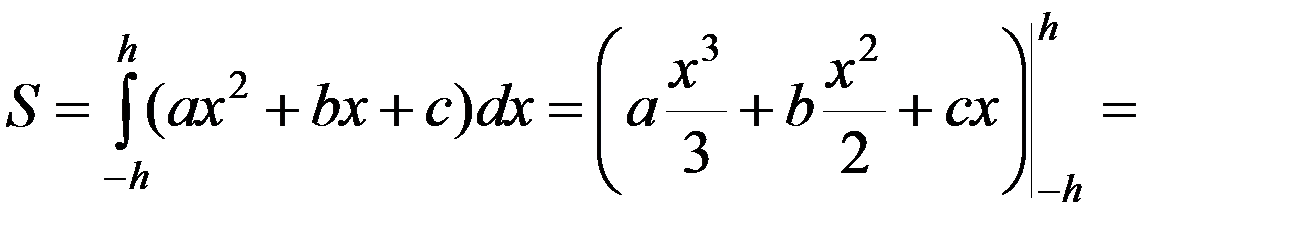
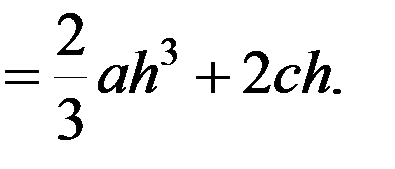
Выражаем S через h, у 0, у 1, у 2. Из (2) следует:
c = у 1, 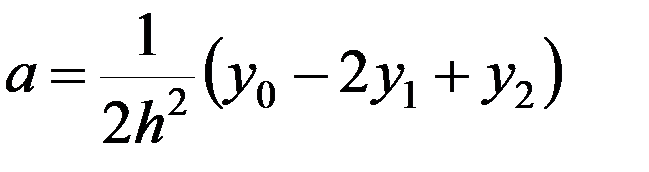 .
.
Тогда
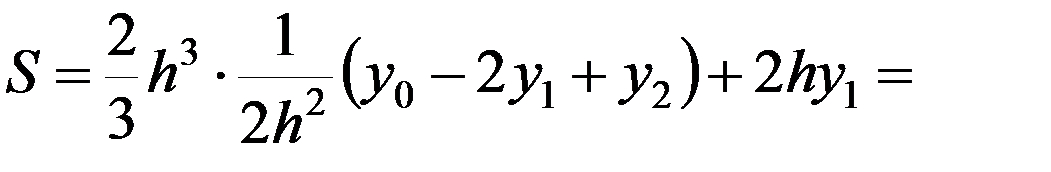
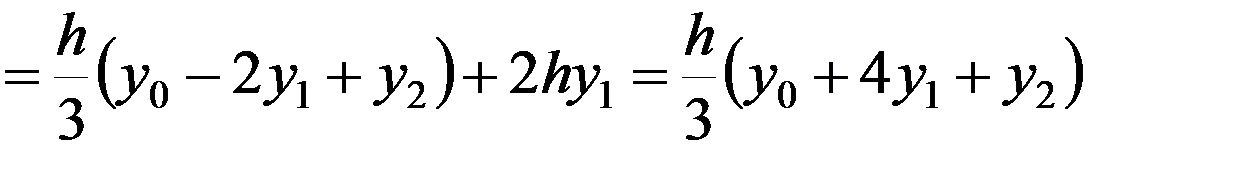 . (3)
. (3)
2. Находим формулу парабол для вычисления интеграла.
а). Отрезок [ a; b ] разбиваем на 2 n равных частей длиной
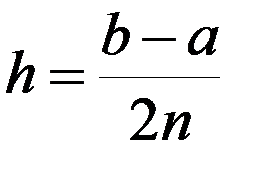 .
.
Абсциссы точек деления a = x 0, x 1, x 2,…, x 2 n –2, x 2 n –1, x 2 n = b:
xi = a + hi.
Значения функции в точках деления: y 0 = f (a), y 1 = f (x 1),
y 2 = f (x 2), …, y 2 n –2 = f (x 2 n –2), y 2 n –1 = f (x 2 n –1), y 2 n = f (b).
б). Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными h, одной элементарной параболической трапецией с основанием, равным 2 h.
На отрезке [ x 0; x 2] парабола проходит через три точки (x 0; y 0), (x 1; y 1), (x 2; y 2). По формуле (3):
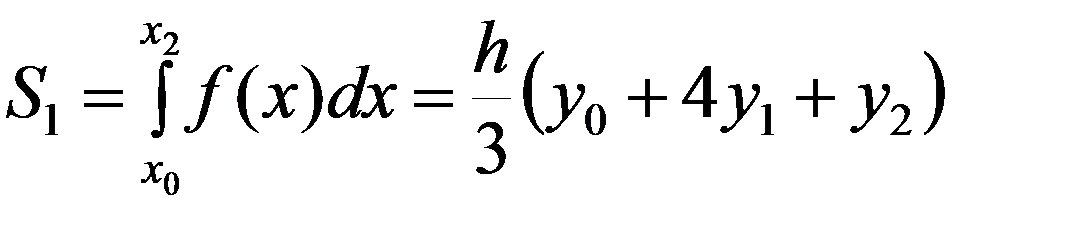 ,
,
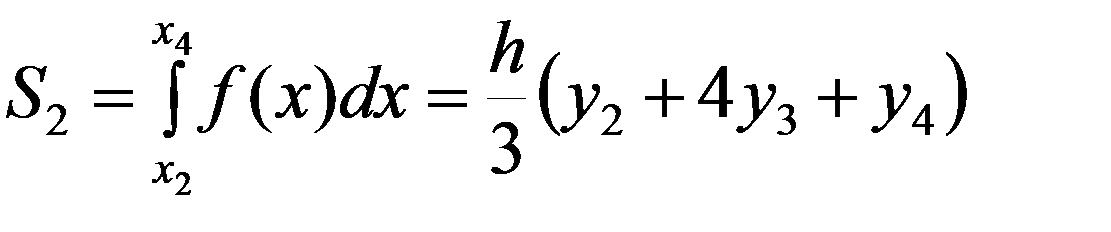 ,
,
…
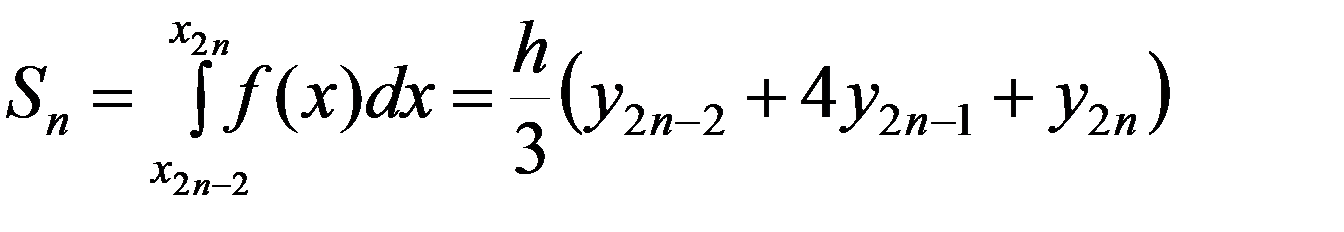 .
.
в). Находим приближенное значение интеграла:
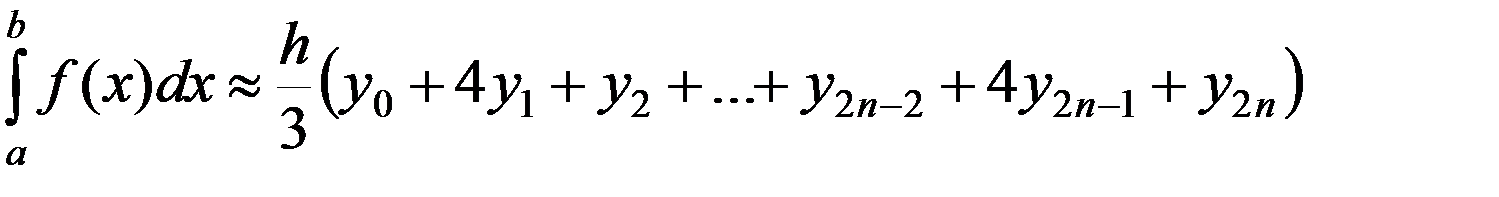
или
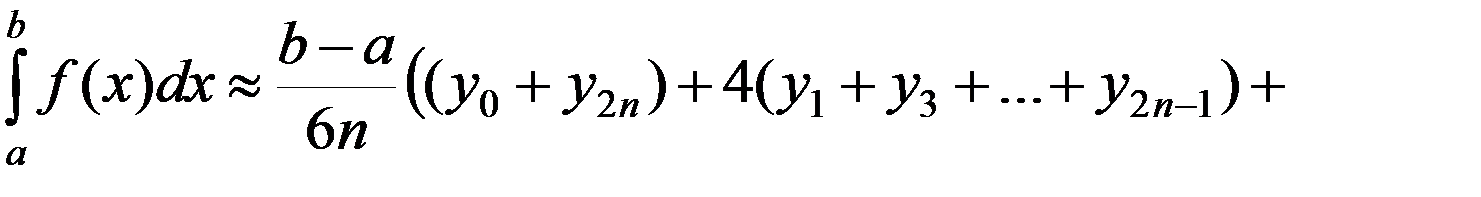
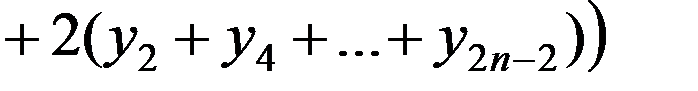 . (4)
. (4)
Выражение (4) называется формулой парабол (или формулой Симпсона).
Абсолютная погрешность приближения по формуле (4) оценивается соотношением
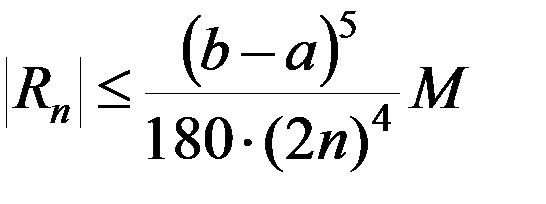 ,
,
где 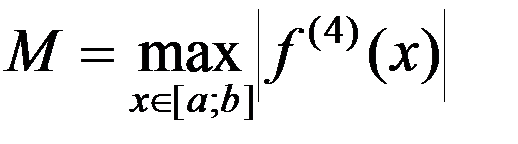 .
.
Формула (4) дает точное значение интеграла, если
y = a 0 x + a 1,
y = a 0 x 2 + a 1 x + a 2,
y = a 0 x 3 + a 1 x 2 + a 2 x + a 3,
так как 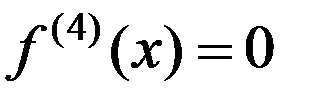 .
.
Пример 1. Вычислить 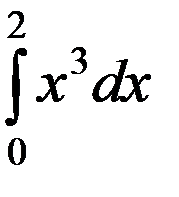 , если отрезок [0;2] разбивается на 4 части.
, если отрезок [0;2] разбивается на 4 части.
Решение ▼ f (x)= x 3.
a = x 0 =0, y 0 =0;
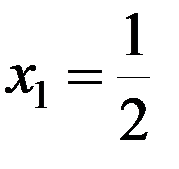 ,
, 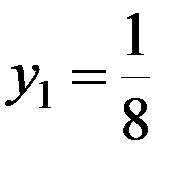 ;
;
x 2 =1, y 2 =1;
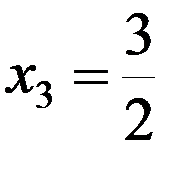 ,
, 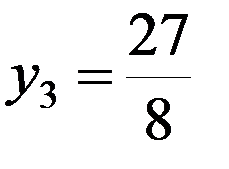 ;
;
b= x 4 = 2, y 4 = 8.
а). По формуле трапеций
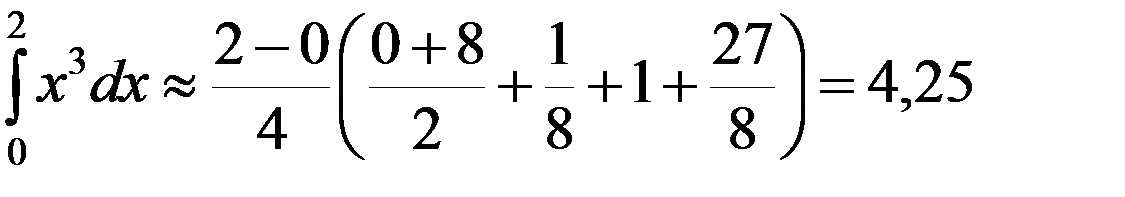 .
.
б). По формуле Симпсона
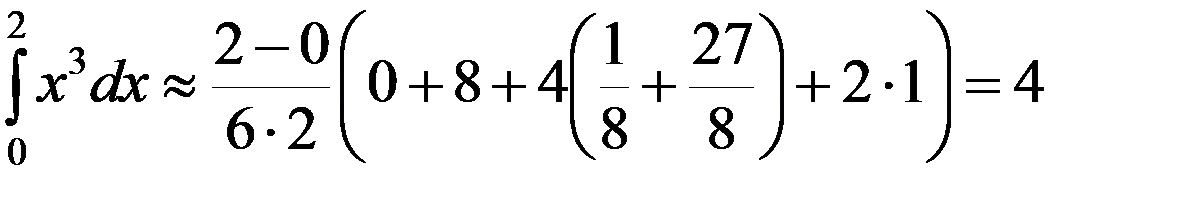 .
.
Точное значение интеграла
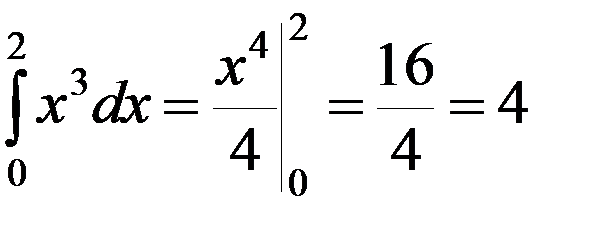 .
.
▲
 2018-02-14
2018-02-14 430
430







