К КОНТРОЛЬНОЙ РАБОТЕ № 8
1. Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?
2. Дайте определение суммы и произведения событий. Сформулируйте теоремы сложения и умножения вероятностей.
3. Запишите формулу полной вероятности.
4. Приведите формулу Байеса.
5. Дайте определение последовательности независимых испытаний. Запишите формулу Бернулли.
6. Дайте определение случайной величины.
7. Дайте определение функции распределения и плотности распределения случайной величины. Сформулируйте их свойства. Приведите примеры.
8. Дайте описание дискретных и непрерывных распределений: равномерное, биномиальное, нормальное.
9. Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному или равномерному закону.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Контрольная работа № 7 «Числовые и функцииональные ряды. Операционное исчисление»
Задача № 1
Исследуйте сходимость числового ряда.

 1.
1. 
 . 11.
. 11. 
 .
.
2. 
 . 12.
. 12. 
 .
.
3. 
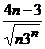 .
.  13.
13. 
 .
.
4. 
 . 14.
. 14. 
 .
.
5. 
 . 15.
. 15. 
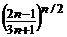 .
.
6. 
 . 16.
. 16. 
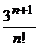 .
.
7. 
 . 17.
. 17. 
 .
.
8. 
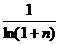 . 18.
. 18. 
 .
.
.9. 
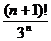 . 19.
. 19. 
 .
.
10. 
 . 20.
. 20. 

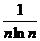 .
.
Задача №2.
Найдите область сходимости степенного ряда.
1. 
 . 11.
. 11. 
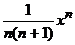 .
.
2. 
 . 12.
. 12. 
 .
.
3. 
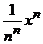 . 13.
. 13. 
 .
.
4. 
 . 14.
. 14. 
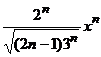 .
.
5. 
 . 15.
. 15. 
 .
.
6. 
 . 16.
. 16. 
 .
.
7. 
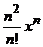 . 17.
. 17. 
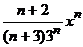 .
.
8. 
 . 18.
. 18. 
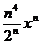 .
.
9. 
 . 19.
. 19. 
 .
.
10. 
 . 20.
. 20. 
 .
.
Задача № 3.
Вычислите приближенно определенный интеграл, взяв шесть первых слагаемых разложения подынтегральной функции в ряд Маклорена и затем проинтегрировав их почленно
1. 
 dx. 11.
dx. 11. 
 dx.
dx.
2. 
 dx. . 12.
dx. . 12. 
 dx.
dx.
3. 
 dx. 13.
dx. 13. 
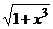 dx.
dx.
4. 
 dx. 14.
dx. 14. 
 dx.
dx.
5. 
 dx. 15.
dx. 15. 
 dx.
dx.
6. 
 dx. 16.
dx. 16. 
 dx.
dx.
7. 
 dx. 17.
dx. 17. 
 dx.
dx.
8. 
 dx. 18.
dx. 18. 
 dx.
dx.
9. 
 dx. 19.
dx. 19. 
 dx.
dx.
10. 
 dx. 20.
dx. 20. 
 dx.
dx.
Задача № 4
Разложите данную функцию f (x) в ряд Фурье
1. f (x) = 2 x,(–  ,
,  ). 11. f (x) = sin (x / 2), (0,
). 11. f (x) = sin (x / 2), (0,  ).
).
2. f (x) =  12. f (x) =
12. f (x) = 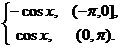
3. f (x) = 2 – x,(–5, 5). 13. f (x) = 1 + cos (x/ 2), ( , 2
, 2  ).
).
4. f (x) =| x –1|, (0, 2). 14. f (x) = – | x |, (0, 1).
5. f (x) =  15. f (x) =
15. f (x) = 
6. f (x) = | x |, (-1, 1). 16. f (x) = sin (x /2),(-  ,
,  ).
).
7. f (x) = 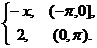 17. f (x) =
17. f (x) = 
8. f (x) =| x | + 2,(-  ,
,  ). 18. f (x) = – | x | + 2, (-2,2).
). 18. f (x) = – | x | + 2, (-2,2).
9. f (x) = x + 3, (–  ,
,  ). 19. f (x) =| 10 – x |, (5,15).
). 19. f (x) =| 10 – x |, (5,15).
10. f (x) =  20. f (x) =
20. f (x) = 
Задача № 5
Найдите изображение по Лапласу функции f (t).
1. 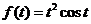 ; 11.
; 11.  ;
;
2.  ; 12.
; 12.  ;
;
3.  ; 13.
; 13.  ;
;
4.  ; 14.
; 14.  ;
;
5.  ; 15.
; 15.  .
.
6. 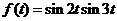 , 16.
, 16. 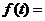

7. 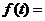
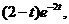 17.
17. 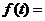

8. 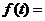
 18.
18. 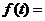

9. 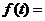
 19.
19. 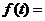
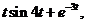
10. 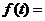
 20.
20. 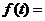

Задача №6.
Найдите оригинал по заданному изображению
1. 
 ,
,
 ,
,  ,
,
3. 
 ,
,
, 
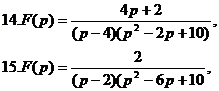
 , 16.
, 16. 
 ,
,  ,
,
 ,
,  ,
,
9.  19.
19. 
10. 
 .
.
Задача № 7.
Методом операционного исчисления найдите частное решение дифференциального уравнения или системы дифференциальных уравнений, удовлетворяющее начальным условиям.
1.  ; 6.
; 6. 
х (0) = 0,  1. х (0) = 0,
1. х (0) = 0,  1.
1.
2.  7.
7. 
х (0) = 0,  1. х (0) = 1;
1. х (0) = 1;  0.
0.
3.  8.
8. 
х (0) = 0;  0. х (0) = 0,
0. х (0) = 0,  0.
0.
4.  9.
9. 
х (0) = 0,  0. х (0) = 0,
0. х (0) = 0,  0.
0.
5.  10.
10. 
х (0) = 0,  0. х (0) = 1,
0. х (0) = 1,  0.
0.
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
 2018-02-12
2018-02-12 262
262








