Комплексное сопротивление
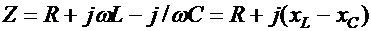
как и всякий комплекс можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать z, т.е. Z=zejψ. Точку над Z не ставят, так как ее принято ставить только над теми комплексными величинами, которые отображают синусоидальные функции времени.
В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть jХ:
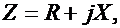
| (10.12) |
где R – активное сопротивление; X – реактивное сопротивление.
Под комплексной проводимостью Y понимают величину, обратную комплексному сопротивлению Z:

| (10.13) |
Действительную часть ее обозначают через g, мнимую – через b. Так как
 , ,
|
то
  
| (10.14) |
Если X положительно, то и b положительно. При X отрицательном b также отрицательно.
При использовании комплексной проводимости закон Ома записывают так:
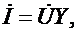 или или 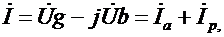
| (10.15) |
Модуль комплексного сопротивления  , а комплексной проводимости
, а комплексной проводимости 
 Следовательно, z и y можно представить гипотенузами прямоугольных треугольников (рис.10.3), называемых соответственно треугольником сопротивлений и треугольником проводимостей.
Следовательно, z и y можно представить гипотенузами прямоугольных треугольников (рис.10.3), называемых соответственно треугольником сопротивлений и треугольником проводимостей.
Треугольники сопротивлений и проводимостей дают графическую интерпретацию связи между модулями полного сопротивления z и полной проводимости y и их составляющими.
 2018-02-13
2018-02-13 276
276








