а) Изображение константы
Пусть 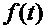 = А =const. Тогда
= А =const. Тогда

| (25.1) |
Следовательно изображение константы равно этой константе, деленной на р, то есть А 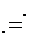 А / p.
А / p.
б) Изображение показательной функции
Пусть 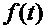 =
=  . Тогда
. Тогда

| (25.2) |
т.е. 
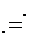
 .
.
Если  то
то 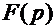
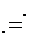
 . Положим,
. Положим,  , тогда
, тогда

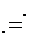
 но
но  следовательно
следовательно

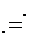
 , откуда
, откуда


 ;
; 



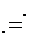
 .
.
Изображение комплекса синусоидального тока

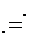
 а напряжения
а напряжения 

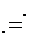

в) Изображение производной
Допустим, дана некоторая функция 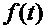 и известно ее изображение
и известно ее изображение 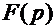 . Найдем изображение производной этой функции. Пусть
. Найдем изображение производной этой функции. Пусть  , и требуется найти ее изображение Ф (р). Тогда
, и требуется найти ее изображение Ф (р). Тогда

Интегрируя по частям, получим

Так как  (согласно условию существования интеграла Лапласа). Итак, изображение производной имеет вид
(согласно условию существования интеграла Лапласа). Итак, изображение производной имеет вид

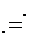

где f (0) – значение функции f (t) при t =0.
Вычисление производной функции при нулевых начальных условиях  соответствует умножению изображения функции на множитель р
соответствует умножению изображения функции на множитель р
 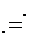 
| (25.3) |
Таким образом, операция дифференцирования оригинала заменяется для изображений операцией умножения изображения на р.
г) Изображение интеграла
Известно изображение некоторой функции 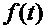 . Требуется определить изображение функции, являющейся интегралом функции
. Требуется определить изображение функции, являющейся интегралом функции 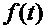 :
:

Так как 

 а
а  , то
, то
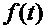
 p
p 
Но изображение 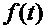
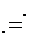
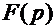 известно. Следовательно можно записать
известно. Следовательно можно записать

Таким образом, окончательно имеем
 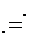 
| (25.4) |
Интегрированию функции 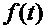 в пределах от 0 до t соответствует деление изображения этой функции на p.
в пределах от 0 до t соответствует деление изображения этой функции на p.
Законы Ома и Кирхгофа в операторной форме при
 2018-02-13
2018-02-13 642
642








