Расчет полей методом зеркальных изображений

На практике часто требуется рассчитывать электрические поля зарядов, расположенных вблизи поверхностей раздела двух или нескольких сред. Трудность таких расчетов состоит в том, что на поверхностях раздела появляются наведенные заряды, закон распределения которых неизвестен. Для задач с границами раздела сред в виде плоскости, цилиндра или сферы эту трудность удается преодолеть применением метода зеркальных изображений.

В соответствии с этим методом исходная сложная задача, в которой поле должно рассчитываться в нескольких средах, сводится к эквивалентным простым задачам расчета полей в однородной среде. Поскольку при замене сред устраняются наведенные на поверхностях раздела заряды, их действие учитывается введением в расчет фиктивных зарядов. Величина, знак и расположение фиктивных зарядов находятся из граничных условий исходной задачи.

 

Поле заряженной оси, расположенной вблизи проводящей

плоскости

 

Пусть заряженная ось (τ – заряд на единицу длины) расположена в диэлектрике параллельно поверхности проводящей среды (рис.41.1,а). Требуется определить характер поля в верхней полуплоскости (диэлектрике).

В результате электростатической индукции на поверхности проводящего тела выступают заряды. Плотность их меняется с изменением координаты x. Поле в диэлектрике создается не только заряженной осью, но и зарядами, выступившими на поверхности проводящего тела. Несмотря на то, что распределение плотности зарядов на поверхности проводящей среды неизвестно, задача сравнительно легко решается методом зеркальных изображений.

Поместим в точке m фиктивный заряд обратного знака (- τ) по отношению к заданному заряду. Расстояние h от точки m до плоскости раздела сред такое же, как и расстояние от действительного заряда до плоскости раздела. В этом смысле осуществлено зеркальное изображение.

Убедимся, что напряженность поля от двух зарядов (τ и –τ) в любой точке границы раздела имеет только нормальную к границе составляющую и не имеет тангенциальной. Действительно, тангенциальные составляющие от обоих зарядов имеют противоположные направления и в сумме дают нуль в любой точке поверхности раздела.

Можно убедиться в том, что потенциал от каждой из осей удовлетворяет уравнению Лапласа.

Так как потенциал от каждой из осей удовлетворяет уравнению Лапласа и в то же время выполняется граничное условие, то на основании теоремы единственности полученное решение является истинным.

Картина поля заряженной оси, расположенной параллельно проводящей плоскости, показана на рисунке 41.1,б. Силовые линии перпендикулярны поверхности провода и поверхности проводящей плоскости. Знаки минус на поверхности проводящей плоскости означают отрицательные заряды, выступившие на ее поверхности в результате электростатической индукции.

 

Электростатическое поле системы заряженных тел,

расположенных вблизи проводящей плоскости

 

В качестве системы заряженных тел рассмотрим многопроводную линию из n весьма длинных проводов с зарядом τ_k на единицу длины линии, протянутых параллельно проводящей поверхности. Высота подвеса и радиус каждого провода известны, а также известна диэлектрическая проницаемость ε_а среды, окружающей провода.

Возьмем в диэлектрике некоторую произвольную точку М (рис.41.2) и найдем ее потенциал. Потенциал точки М будет равен сумме потенциалов, создаваемых каждым проводом и его зеркальным изображением. Составляющую потенциала точки М от провода 1 и его зеркального изображения можно записать следующим образом:

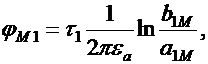
где b_1M – расстояние точки М до зеркального изображения первого провода; a_1M – расстояние точки М до первого провода.

Полагаем, что высота подвеса каждого провода над проводящей поверхностью много больше радиуса проводов. При этом электрические оси практически совпадают с геометрическими.

Составляющая потенциала точки М от второго провода и его зеркального изображения

Таким образом,

1.1.1. Потенциальные коэффициенты

 

Поместим точку М на поверхность первого провода. Тогда  – расстояние первого провода до зеркального изображения второго провода;  – расстояние первого провода до второго и т.д.:

(41.1)

Коэффициенты при зарядах зависят только от геометрических размеров тел, их взаимного расположения и свойств среды. Они не зависят ни от значений, ни от знаков зарядов и потенциалов.

Для сокращения записи выражение (41.1) и другие, аналогичные ему, запишем следующим образом:

 

(41.2)

В этих уравнениях

(41.3)

Коэффициенты  называют потенциальными коэффициентами, а систему уравнений (41.2) – первой группой формул Максвелла. Так как у всех коэффициентов  под знаком логарифма находится дробь, числитель которой всегда больше знаменателя, то все коэффициенты  положительны. Система (41.2) позволяет подсчитать потенциалы заряженных тел по известным общим зарядам тел.

 

1.1.2. Емкостные коэффициенты

 

Решим систему (41.2) относительно зарядов, полагая потенциалы и коэффициенты известными:

(41.4)

Коэффициенты  где Δ – определитель системы (41.2):

 

Алгебраическое дополнение  получают из определителя системы Δ путем вычеркивания k -ой строки и n -столбца и умножения полученного минора на (-1)^k+n

Систему (41.4) называют второй группой формул Максвелла.

Коэффициенты β называют емкостными коэффициентами. Их единица обратная единице коэффициента α. Так как определитель системы симметричен относительно главной диагонали, то  и потому . Все β с одинаковыми индексами положительны, а с разными индексами отрицательны.

 

1.1.3. Частичные емкости

 

Систему уравнений (41.4) принято записывать и в иной форме: так, чтобы в правой части каждой строки были не потенциалы, а разности потенциалов между данным телом и всеми остальными, в том числе и проводящей плоскостью.

В соответствии с (41.4) заряд k -го тела

Слагаемое

 

Поэтому

Обозначим:

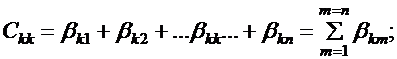	(41.5)
	(41.6)

Тогда

(41.7)

Если придать k значения 1, 2, 3,..., то получим

(41.8)

Система (41.8) является третьей группой формул Максвелла. Коэффициенты C_kk называют собственными частичными емкостями, а коэффициенты C_km – взаимными частичными емкостями. Так как 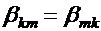, то и

Единица измерения частичных емкостей та же, что и единица измерения емкостных коэффициентов β. Все частичные емкости положительны. Так как  а < 0, то, очевидно, что C_km > 0.

 

Вопросы для самоконтроля

1. Дайте обоснование методу зеркальных изображений.

2. Охарактеризуйте поле заряженной оси, расположенной вблизи проводящей плоскости.

3. Рассмотрите систему заряженных тел, расположенных вблизи проводящей плоскости и получите первую группу формул Максвелла.

4. На основании первой группы формул Максвелла получите вторую группу формул Максвелла.

5. Что определяют потенциальные и емкостные коэффициенты и частичные емкости?

6. Получите третью группу формул Максвелла.

7. Какие частичные емкости называют собственными, а какие – взаимными?